
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывность функции двух переменных в точкеОсновные понятия и определения Пусть на некотором подмножестве D Определение по Коши.Функция z = f(x,y) называется непрерывной в точке Определение через предел.Функция z = f(x,y) называется непрерывной в точке
При этом должны соблюдаться следующие три условия: 1) функция должна быть определена в точке 2) предел функции 3) этот предел должен равняться значению функции z = f(x,y)при x = Определение на языке приращений.Функция z = f(x,y) называется непрерывной в точке
Точка Для функций двух переменных справедливы теоремы о непрерывных функциях одной переменной. Примеры
Пример 11.Исследовать функцию
Решение. 1) 2) Проверим, существует ли общий предел в данной точке:
Используем тригонометрическую формулу
и первый замечательный предел:
Общий предел существует. 3) Ответ:функция терпит разрыв в точке
Пример 12.Исследовать функцию
Решение. 1)  2)
Перейдём к полярным координатам: Если
Общий предел существует. 3)
Ответ:функция непрерывна в точке
Пример 13.Исследовать функцию
Решение. 1) 2)
3)
Ответ:функция непрерывна в точке Пример 14.Исследовать функцию
Решение. 1) 2) Проверим, существует ли общий предел в данной точке:
Используем тригонометрическую формулу
и первый замечательный предел:
3)
Ответ: функция непрерывна в точке
Непрерывность функции нескольких переменных в точке |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 179. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 определена функция z = f(x,y)и точка
определена функция z = f(x,y)и точка  принадлежит этому подмножеству.
принадлежит этому подмножеству. .
. равен значению функции при x =
равен значению функции при x =  , y =
, y =  :
:

 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  , т.е.
, т.е.
 на непрерывность в точке
на непрерывность в точке  .
.
 – функция определена в точке
– функция определена в точке 


 ⇒ функция не является непрерывной в точке
⇒ функция не является непрерывной в точке  .
.
 – функция определена в точке
– функция определена в точке  .
.
 .
.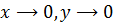 , то
, то  .
.
 ⇒ функция является непрерывной в точке
⇒ функция является непрерывной в точке  [5, с. 179].
[5, с. 179]. .
.
 – функция определена в точке
– функция определена в точке 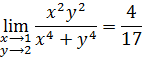

 [4, с. 164].
[4, с. 164]. .
.
 – функция определена в точке
– функция определена в точке 



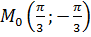 [5, с. 178].
[5, с. 178].