
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные понятия и определенияСтр 1 из 3Следующая ⇒ СОДЕРЖАНИЕ ВВЕДЕНИЕ. 3 § 1. Непрерывность функции одной переменной в точке. 5 1.1. Основные понятия и определения. 5 1.2. Примеры.. 6 § 2. Непрерывность функции двух переменных в точке. 15 2.1. Основные понятия и определения. 15 2.2. Примеры.. 16 § 3. Непрерывность функции нескольких переменных в точке. 20 3.1 Основные понятия и определения. 20 ЗАКЛЮЧЕНИЕ. 22 СПИСОК ЛИТЕРАТУРЫ.. 23 ВВЕДЕНИЕ
Актуальность исследования.Оценивая неизбежные с течением времени изменения в окружающем мире, мы пытаемся проанализировать происходящие процессы, чтобы выделить их наиболее существенные черты. Один из первых на этом пути встает вопрос: как происходят характерные для этого явления изменения – непрерывно или дискретно, т.е. скачкообразно. Равномерно ли понижается курс валюты или обваливается, происходит постепенная эволюция или революционный скачок? Чтобы унифицировать качественные и количественные оценки происходящего, следует абстрагироваться от конкретного содержания и изучить проблему в терминах функциональной зависимости. К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны (непрерывны), и зависимость, например, пути s от времени t, выраженная законом s = f(t), даёт пример непрерывной функции f(t). Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t). К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые сплошные среды — твердые, жидкие или газообразные, например металлы, воду, воздух. Всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды без всяких просветов, непрерывно распределенной в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности играет в этих дисциплинах, как и во многих других, большую роль[6, с. 127].  Объект исследования:функции n-переменных. Предмет исследования:непрерывность функции в точке. Цель курсовой работы:исследовать на непрерывность функции одной переменной и двух переменных в точке. Основные задачи исследования: 1. Определить основные понятия непрерывности функции в точке для функции одной переменной и исследовать этот вид функций на непрерывность в точке. 2. Определить основные понятия непрерывности функции в точке для функции двух переменных и исследовать этот вид функций на непрерывность в точке. 3. Определить основные понятия непрерывности функции в точке для функции нескольких переменных. Основные методы исследования:изучение литературы по теме, самостоятельное решение задач. Практическая значимостьпроведённого исследования состоит в том, что в нём подобран материал по теме курсовой работы и решены задачи. На защиту выносится:теоретический и практический материал по теме исследования. Курсовая работа состоит из введения, трех параграфов и заключения. Список литературы содержит 7наименований.
Непрерывность функции одной переменной в точке Основные понятия и определения Пусть на некотором промежутке X определена функция y = f(x)и точка Определение по Коши.Функция y = f(x) называется непрерывной в точке Определение через предел.Функция y = f(x) называется непрерывной в точке
При этом должны соблюдаться следующие три условия: 1) функция должна быть определена в точке 2) предел функции 3) этот предел должен равняться значению функции y = f(x)при x = Замечание.Существование
Определение на языке приращений.Функция y = f(x) называется непрерывной в точке
Точка Если условие непрерывности функции в точке Теорема 1.Пусть функции f(x) и g(x) непрерывны в точке Теорема 2.Пусть функции f(x) и g(x) непрерывны в точке Теорема 3.Пусть функция
Примеры Пример 1.Исследовать на непрерывность функцию Решение. Для исследования применим определение (1.2). Приращение аргумента равно
Условия определения (1.2) выполнены, а значит, функция Ответ: функция непрерывна в точке Пример 2.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Предел функции при Ответ: функция непрерывна в точке x = 3 [1, c. 166].
Пример 3.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Условия определения (1.1) выполнены ⇒ функция Ответ: функция непрерывна в точке x = 2 [1, с. 166].
Пример 4.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Условия определения (1.1) выполнены ⇒ функция Ответ:функция непрерывна в точке x = 1[1, с. 166].
Пример 5.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Условия определения (1.1) выполнены ⇒ функция Ответ: функция непрерывна в точке x = Пример 6.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Условия определения (1.1) выполнены ⇒ функция Ответ: функция непрерывна в точке x =
Пример 7.Исследовать на непрерывность функцию Решение.Для исследования применим определение (1.1).
Условия определения (1.1) выполнены ⇒ функция Ответ: функция непрерывна в точке x =
Пример 8.Функция f (x)определена следующим образом:
Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0, x = 1, x = 3? Решение.Проверим все три условия непрерывности функции в каждой граничной точке. 1) Найдём левосторонний предел в этой точке:
Найдём правосторонний предел в этой точке:
Предел функции должен быть найден при той ветви функции, которая включает в себя точку x = 0. Найдём его:
Предел функции при 2) Найдём левосторонний предел в этой точке:
Найдём правосторонний предел в этой точке:
Предел функции должен быть найден при той ветви функции, которая включает в себя точку x = 1. Найдём его:
Предел функции при 3) Найдём левосторонний предел в этой точке:
Найдём правосторонний предел в этой точке:
Предел функции должен быть найден при той ветви функции, которая включает в себя точку x = 3. Найдём его:
Предел функции при Ответ:данная функция является непрерывной в каждой граничной точке[2, с.186].
Пример 9.Дана функция:
Исследовать функцию на непрерывность в точках x = 0, x = Решение. 1) Исследуем на непрерывность точку x = 0.
Вычислим односторонние пределы:
Вычислим общий предел:
Предел функции при 2) Исследуем на непрерывность точку x =
Вычислим односторонние пределы:
Вычислим общий предел:
Предел функции при Ответ:функция непрерывна в точках x = 0, x =
Пример 10.Дана функция:
Исследовать функцию на непрерывность в точках x = -2, x = 2. Решение. 1) Исследуем на непрерывность точку x = -2.
Вычислим односторонние пределы:
Так как нарушено условие непрерывности функции в точке ⇒ функция не является непрерывной в точке x = -2. 2) Исследуем на непрерывность точку x = 2.
Вычислим односторонние пределы:
Так как нарушено условие непрерывности функции в точке ⇒ функция не является непрерывной в точке x = 2. Ответ:функция не является непрерывной в точках x = -2, x = 2[4, с. 164].
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 177. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 принадлежит этому промежутку.
принадлежит этому промежутку. [7,с.108].
[7,с.108]. равен значению функции при x =
равен значению функции при x = 
 ;
; должен существовать;
должен существовать;
 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  , т.е.
, т.е.
 непрерывна в точке
непрерывна в точке 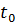 и функция f(x) непрерывна в точке
и функция f(x) непрерывна в точке  . Тогда сложная функция
. Тогда сложная функция  непрерывна в точке
непрерывна в точке  в точке
в точке  .
. , тогда приращение функции в этой точке равно:
, тогда приращение функции в этой точке равно: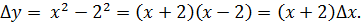

 при x = 3.
при x = 3.


 равен значению функции при x = 3, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция
равен значению функции при x = 3, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция  в точке x = 2.
в точке x = 2.


 в точке x = 1.
в точке x = 1.


 в точке x =
в точке x =  .
.


 в точке x =
в точке x =  .
.
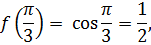

 в точке x =
в точке x = 

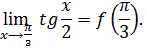

 – функция определена в точке x = 0.
– функция определена в точке x = 0.



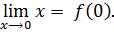
 равен значению функции при x = 0, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция в точке x = 0 непрерывна.
равен значению функции при x = 0, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция в точке x = 0 непрерывна. – функция определена в точке x = 1.
– функция определена в точке x = 1.




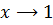 равен значению функции при x = 1, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция в точке x = 1 непрерывна.
равен значению функции при x = 1, при этом соблюдаются условия применимости определения (1.1). Следовательно, функция в точке x = 1 непрерывна. – функция определена в точке x = 3.
– функция определена в точке x = 3.





 .
. – функция определена в точке x = 0.
– функция определена в точке x = 0.



 – функция определена в точке x =
– функция определена в точке x = 




 равен значению функции при x =
равен значению функции при x = 
 – функция определена в точке x = -2.
– функция определена в точке x = -2.


 – функция определена в точке x = 2.
– функция определена в точке x = 2.

