
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Поверхности, образуемые вращением кривых второго порядка вокруг их осей1. Сфера образуется вращением окружности вокруг ее диаметра (рис. 2.3.49). Рис. 2.3.49 4. Однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси. Эта поверхность образуется также вращением прямой (рис. 2.3.48 справа).
Тором называется поверхность, образованная вращением окружности вокруг оси, принадлежащей плоскости окружности, но не проходящей через ее центр. При этом ось вращения может пересекать окружность, касаться ее и располагаться вне окружности. В первых двух случаях тор называется закрытым, в последнем - открытым, или кольцом. На рис. 2.3.50 изображены проекции тора-кольца.  Рис. 2.3.50,1(анимационный) при составлении алгоритма решения этой группы задач следует базироваться на свойстве (3) из § 38, т. е. для того чтобы на чертеже поверхности указать проекции принадлежащей ей точки, необходимо вначале построить проекции какой-либо линии, принадлежащей поверхности, а затем на этой линии отметить точку. В качестве линии, как правило, выбирается образующая поверхности. Если поверхность может быть получена образующей различной формы, то предпочтение следует отдавать наиболее простым и удобным для построения линиям: окружностям для поверхностей вращения, прямым для линейчатых поверхностей (в частности, для плоскости целесообразно использовать линии уровня*). 13. В сечении поверхности плоскостью получается плоская линия, которую строят по отдельным точкам. При этом сначала строят опорные точки, лежащие на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. Если проекция линии пересечения этими точками не определяется полностью, то строят, дополнительны, промежуточные между опорными, точки. Чертеж всегда можно преобразовать так, чтобы секущая плоскость стала проецирующей (см. рис. 8), поэтому рассмотрим случаи пересечения поверхностей, плоскостями частного положения, считая секущую плоскость прозрачной. В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии (рис. 8.1). 14. Сечение поверхности плоскостью представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности. При пересечении плоскостью многогранника (например призмы, пирамиды и т.д.) в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника. Проекциями сечения многогранников, в общем случае, являются многоугольники, вершины которых принадлежат ребрам, а стороны – граням многогранника. Поэтому задачу по определению сечения многогранника можно свести к многократному решению задачи по определению точки встречи прямой (ребер многогранника) с секущей плоскостью или к задаче по нахождению линии пересечения двух плоскостей (грани многогранника и секущей плоскости). Первый путь решения называют способом ребер, второй – способом граней. Какому из способов следует отдать предпочтение, надо решать в каждом конкретном случае. Первый способ предпочтителен, если некоторые ребра многогранника являются проецирующими, второй – если некоторые грани многогранника являются проецирующими плоскостями. В ряде случаев целесообразно комбинированное применение обоих способов. При построении линии пересечения двух поверхностей способом вспомогательных секущих плоскостей секущие плоскости, принятые в качестве посредников, могут быть и общего, и частного положения. Более широкое применение находят плоскости частного положения. Плоскости общего положения применяются в ограниченных случаях. Например, их удобно использовать при построении линии пересечения конических и цилиндрических, а также пирамидальных и призматических поверхностей общего вида, когда основания этих поверхностей расположены в одной и той же плоскости. 15. В общем случае для графического решения задачи по определению положения точек пересечения (встречи) линйи с поверхностью необходимо выполнить ряд геометрических построений в приведенной ниже последовательности: заключить данную линию во вспомогательную поверхность; определить линию пересечения этой вспомогательной поверхности с заданной поверхностью; отметить точки, в которых пересекаются полученная линия с заданной (рис. 238).
Рис. 237 * Эта теорема известна также как "теорема Монжа", по имени основоположника начертательной геометрии Гаспара Монжа, доказавшего эту теорему. Запишем указанную последовательность решения в виде табл. 9 (как это сделано в § 43 при составлении алгоритма для решения задачи по определению линии пересечения двух поверхностей). В правой части таблицы приведена символическая запись, соответствующая смысловому содержанию отмеченных этапов решения. Таблица 9 Таблица 9
Алгоритм для решения задачи определения точек пересечения линии с поверхностью в символической форме можно записать: [К, ...] = (ГП а) Па. Здесь, как и у алгоритма определения линии пересечения двух поверхностей, в зависимости от порядка и взаимного расположения заданных кривой и поверхности множество искомых точек {К, ...J может состоять из одной, двух и более точек. Полученный алгоритм является универсальным, пригодным для решения задачи с любым вариантом задания исходных данных. Рассмотрим различные варианты решения задачи: 1. Пересечение кривой с поверхностью. 2. Пересечение кривой с плоскостью. 3. Пересечение прямой с поверхностью. 4. Пересечение прямой с плоскостью. 16. Эта задача является обобщением рассмотренной ранее задачи на построение линии пересечения двух плоскостей. Ее решают путем введения вспомогательных поверхностей посредников. Построение линии пересечения двух поверхностей надо выполнять по приведенному ниже алгоритму: Выбрать вспомогательную поверхность Гтаким образом, чтобы она пересекала заданные поверхности и Л (рис. 9);
Для более точного построения искомой линии пересечения выбирается ряд вспомогательных поверхностей, находятся точки искомой линии пересечения, которые последовательно соединяются. Способ секущих плоскостей Рассмотрим частный случай – способ вспомогательных ПРОЕЦИРУЮЩИХ плоскостей. Он заключается в следующем: вводится ряд плоскостей частного положения (уровня или проецирующих), пересекающих данные поверхности по графически простым линиям (прямым или окружностям). Пересечение этих линий между собой дает точки, которые будут общими для каждой из данных поверхностей и, следовательно, будут принадлежать искомой линии пересечения. Метод вспомогательных секущих плоскостей заключается в том, что обе пересекающиеся поверхности мысленно рассекаются вспомогательной плоскостью (плоскостью-посредником). Такая плоскость рассечет обе поверхности по каким-то линиям, которые в пересечении дадут общие точки, принадлежащие линии пересечения. При выборе вспомогательных секущих плоскостей следует стремиться к тому, чтобы обе поверхности пересекались по линиям, простым для построения (прямым, окружностям). Пересечение цилиндрических поверхностей.Цилиндрические поверхности пересекаются между собой в общем случае по кривым линиям. Если две цилиндрические поверхности равного диаметра с пересекающимися осями, с общей плоскостью симметрии, параллельной плоскости проекции, пересекаются, то линия их пересечения в этом случае изобразится на этой плоскости проекции в виде прямолинейных отрезков 18. Представим поверхность в виде тонкой и гибкой, но нерастяжимой пленки. В этом случае некоторые поверхности можно постепенным изгибанием совместить с плоскостью так, что при этом не возникает ни разрывов, ни складок. Поверхности, обладающие этим свойством, называются развертывающимися, а фигура, полученная в результате совмещения поверхности с плоскостью – разверткой данной поверхности. Построение разверток является важной технической задачей, так как в промышленности широко применяются разнообразные изделия, выполненные из листового материала путем изгибания (сосуды, трубопроводы, швейные изделия и др.). В начертательной геометрии развертки поверхностей делятся на:
Для построения разверток многогранников применяются следующие способы: |
||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 242. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
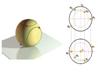 ее оси.
ее оси.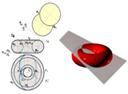 Рис. 2.3.50
Рис. 2.3.50 четвертого порядка.
четвертого порядка. на рис. 2.3.50), на две окружности (меридиан), если плоскость проходит через ось тора(плоскости Г и Г' на рис. 2.3.50), на две окружности, если плоскость проходит через центр тора и касается его меридиана (плоскость
на рис. 2.3.50), на две окружности (меридиан), если плоскость проходит через ось тора(плоскости Г и Г' на рис. 2.3.50), на две окружности, если плоскость проходит через центр тора и касается его меридиана (плоскость 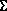 ). Проекции точки, например М, принадлежащей поверхности тора, можно построить при помощи параллели
). Проекции точки, например М, принадлежащей поверхности тора, можно построить при помощи параллели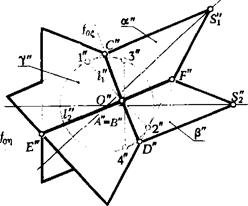
 = m1, Г1
= m1, Г1 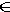 и Л; Г2
и Л; Г2