Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Способ перемены плоскостей проекций.Стр 1 из 3Следующая ⇒ Перемена одной плоскости проекций. Даны проекции точки A (A1 А2) (фиг.257,а).
3. Взаимное положение прямых. Положение прямой линии определяется двумя ее точками. Поэтому пространственная прямая будет задана, если на чертеже имеются проекции двух ее точек, т.к. линии, проходящие через одноименные проекции этих точек, будут проекциями прямой. Прямая относительно плоскостей проекции может занимать различные положения. Прямая общего положения.
Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4 (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций. Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило:расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси. Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости. Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.Положение плоскости относительно плоскостей проекций. К числу основных задач, решаемых на плоскости, относятся: построение прямой в плоскости, построение в плоскости некоторой точки, проверка принадлежности точки плоскости. Решение этих задач основывается на известных положениях геометрии:
5. Понятие об аксонометрических проекциях и их применение.Аксонометрическими (Аксонометрия в переводе с греческого языка («ахоп» — ось; «metreo» — измеряю) означает осемерное изображение.) проекциями называют изображения, полученные путем проектирования параллельными лучами фигуры (предмета) вместе с осями координат на произвольно расположенную плоскость, которую называют «аксонометрической» (или картинной). Обычно плоскость (или предмет) располагают так, чтобы на аксонометрической проекции предмета были видны три стороны: верхняя (или нижняя), передняя и левая (или правая). 6. прямоугольные Аксонометрические проекции, когда направление проецирования перпендикулярно плоскости аксонометрических проекций. Основное предложение аксонометрии сформулировано немецким геометром К. Польке: три произвольной длины отрезка прямых, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных координатных осях от начала.Согласно этой теореме любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые произвольной длины отрезки этих прямых, отложенные от точки их пересечения, можно принять за аксонометрические масштабы.Эта система аксонометрических осей и масштабов является параллельной проекцией некоторой прямоугольной системы координатных осей и натуральных масштабов, т. е. аксонометрические масштабы можно выдавать совершенно произвольно, а коэффициенты искажения при этом связаны следующим соотношением: u2 + v2 = w2 = 2 + + ctg2(p, где ф — угол между направлением проецирования и плоскостью аксонометрических проекций (рис. 156). Для прямоугольной аксонометрии, когда ф = 90°, это соотношение принимает вид и2 + v2 + w2 = 2 (1), т. е. сумма квадратов коэффициента искажения равна двум. При прямоугольном проецировании может быть получена только одна изометрическая проекция и бесконечное множество диметрических и триметрических проекций. ГОСТ 2.317—69 предусматривает применение в инженерной графике двух прямоугольных аксонометрии: прямоугольной изометрии и прямоугольной диметрии с коэффициентами искажения и = w = 2v. 7. под поверхностью понимается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0 , где F(х,у,z) – многочлен n-й степени или трансцендентная функция. Начертательная геометрия изучает геометрические фигуры, заданные графически. Поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Если принять, что положение движущейся в пространстве линии будет непрерывно меняться с течением, например, времени, и принять время за параметр, то поверхность можно рассматривать как непрерывное однопараметрическое множество линий. В свое очередь, линия определяется как непрерывное однопараметрическое множество точек. С учетом этого можно дать следующее определение поверхности: поверхностью называется непрерывное двухпараметрическое множество точек. Способы задания поверхностей Поверхность, образованная каким-либо способом, считается заданной, если относительно произвольной точки пространства можно однозначно решить вопрос о ее принадлежности данной поверхности. Для поверхности, заданной на чертеже, это условие становится следующим: поверхность считается заданной, если по одной проекции точки, принадлежащей поверхности, можно построить вторую проекцию. Совокупность условий, необходимых для задания поверхности, называется определителем поверхности. Он состоит из геометрической и алгоритмической частей. Геометрическая часть определителя – это перечень геометрических элементов и фигур, которые участвуют в образовании поверхности. Алгоритмическая часть определителя описывает взаимосвязи между элементами и фигурами, входящими в геометрическую часть, а также представляет совокупность правил, по которым образуется поверхность. Например, поверхность сферы можно образовать, вращая некоторую точку вокруг другой неподвижной точки (центра сферы) и поворачивая при этом плоскость вращения вокруг оси, проходящей через центр сферы. В этом случае в геометрическую часть определителя войдут две точки, а в алгоритмическую часть – описание правил вращения одной точки вокруг другой. Существует три наиболее распространённых способа задания поверхностей: аналитический, графический и графоаналитический. Рассмотрим каждый из этих способов. Аналитический способ. В этом случае поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют заданному уравнению вида: F(x, y, z) = 0или z = Ф(х, у), где Fи Ф - алгебраическая или трансцендентная функция. Поверхность также может задаваться системой уравнений, определяющих зависимость координат точек поверхности от некоторого параметра: x y = Y(t) z = Z(t). Такой способ задания называется параметрическим. Широкое распространение в последнее время получила векторная форма задания поверхности, в этом случае поверхность определяется вектор-функцией Rнекоторой точки N, принадлежащей поверхности. Эта функция зависит от двух скалярных аргументов u и v: R = R(u,v) = x(u,v)i + y(u,v)j + z(u,v)k, где x,y,z – координаты вектор-функции. Параметры u и v называются криволинейными координатами поверхности. Каждой паре значений u, v из области их изменения соответствует точка поверхности, координаты которой определяются функциями x = x(u,v), y = y(u,v), z = z(u,v). Если один из параметров принять постоянным, например, задаться v=v1, то вектор функции R=R(u,v1) опишет на поверхности некоторую линию v1=const, называемую координатной линией. Переходя к другому значению v=v2, получим следующую линию семейства v2=const. Совокупность линий vi=const (i=1, …, m) образует линейный каркас поверхности (линейным каркасом поверхности называется множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества). Аналогично, фиксируя u и изменяя v, можно получить координатную линию u=const.Множество линий uj=const (j=1, ..., n) образует другой линейный каркас той же поверхности. Через каждую точку поверхности можно провести две координатные линии (одну – семейства uj=const, другую – vi=const).Совокупность двух линейных каркасов образует сетчатый каркасповерхности или сеть. Графический способзадания поверхностей предполагает задание поверхности на комплексном чертеже. При этом, как уже было сказано выше, поверхность считается заданной, а ее чертеж – метрически определенным, если по одной проекции точки, лежащей на поверхности, можно построить другую ее проекцию. Чаще всего поверхность задается на чертеже проекциями элементов своего определителя, т.е. тех геометрических объектов, с помощью которых поверхность была образована. Алгоритмическая часть определителя поверхности переводится при этом в алгоритм графических и аналитических операций, которые необходимо осуществить над проекциями элементов определителя, чтобы построить проекции произвольных точек или линий поверхности. Однако наглядность такого чертежа поверхности очень низкая. Для улучшения наглядности чертеж поверхности приходится дополнять проекциями наиболее характерных или важных точек и линий поверхности, в том числе очерковымилиниями ее проекций. Очерковыми линиями (или очерком) проекций поверхности называются линии, ограничивающие области ее проекций (рис.9.3). Графоаналитический способ. При этом способе задания поверхности часть линий (например, образующая поверхности) может задаваться аналитически в виде уравнения
где 7. В начерт. Геом. Поверхности опред. Как совокупность поседовательных положений линий движущих в пространстве по опред. Закону. При задании поверхности в начерт. Геом. Исходят из кинематического способа. Поверхность нужно задать очерком. Каркас совокупность точек и линий принадлежавших данной поверхности. Поверхности могут быть закономерными и незакономерными. Начерт. Геом. Изучает закономерные поверхности. Чаще всего поверхности закономерные в начер. Геом. Задаются определителем. Определитель – минимальное, но достаточная информация для изображения поверхности на чертеже. Опред. Состоит из двух частей геометрической и алгоритмической. Поле обозначения поверхности геометрическая часть записывается которая содержит обозначение геом. Объеков, которые изображается на чертеже и однозначно задают поверхность. В квадратныъх скобках пишется все то что вы считаете нужным для расшифровки поверхности. Одну и тому поверхность можно задать с разными законами движения в пространстве. Исходя из кинематического образования поверхности дадим определение: образующая-это линия которая при свеем движении образует поверхность. Направляющая-это линия задающая закон перемещение образующей в пространстве. Образующая при своем движении всегда должна пересекать линию направляющую, тогда закон действует. В общем случае направляющих три. 8. При этом общая линия пересечения должна лежать внутри очерка как одной, так и другой поверхности.На чертеже поверхность задают очерком и конечным числом точек или линий, называемых каркасом поверхности.Ограничив длину образующей и изобразив её начальное и конечное положение, получим очерк поверхности.Пересечение параллелей с плоскостью G(OI), параллельной плоскости проекций и проходящей через ось вращения, образует линию, которая называется главным меридианом поверхности и является очерком данной проекции.Очерк поверхности строится с помощью параллелей точек: А, В - параллели основания; G - горло; 1 - точка главного меридиана (1 = [АВ] Лет), являющаяся границей видимости образующей [АВ] на фронтальной проекции; случайные точки (не обозначены на чертеже буквами или цифрами).Очерком поверхности будет огибающая положений образующих и установленные границы - линии на поверхности (образующие, сечения, направляющие или другие линии).Очерком поверхности является парабола.Очерком поверхности является огибающая положений образующих.Очерк цилиндра - прямые, касательные к основаниям, или прямые, соединяющие концы больших осей эллипсов (последнее справедливо только для цилиндров).Найти аксонометрию центров оснований, построить эллипсы оснований и очерк цилиндра.Так строится нужное количество точек, а по ним строятся "проекции оснований и очерк.Очерком конуса являются образующие, проведённые из вершины S' касательно к основанию.В этом случае очерковых образующих конуса нет и говорят об нечезновении очерка, т.Огибающая этих параллелей и будет очерком поверхности.Вершину очерка можно определить более точно по углу аксонометрического проецирования, если в этом есть необходимость. Очерком поверхности будет огибающая аксонометрических проекций вписанных сфер..Очерк поверхности Пересечение профильных очерков определяет опорные точки А3 и Оз.Плоскость у(у2, уз) рассекает тор по параллели и проходит через образующую фронтального очерка цилиндра.Общая плоскость симметрии поверхностей является фронтальной плоскостью уровня, поэтому пересечение фронтальных очерков определяет опорные точки A(Az) и 8(82) линии пересечения.Она рассечет цилиндр по окружности т(гаг), которая изобразится отрезком внутри очерка цилиндра.Точка пересечения очерка сферы с очерком конуса определяет положение параллели p(pi) пересечения сферы с конусом.Вторая точка пересечения очерков сферы и конуса, а следова-тельно.Так строятся все необходимые точки и соединяются плавной кривой с учётом видимости, а затем обводятся очерки поверхностей.Плоскость второй линии пересечения /(/2) тоже будет проецирующей и для её построения достаточно соединить опорные точки Ь и 22 пересечения очерков прямой линией.Очерк поверхности (проекция контура).Проекция контура поверхности называется ее очерком (очертанием).Контур поверхности, а следовательно и очерк, является границей видимости (невидимая часть поверхности р условно затемнена точками, как будто в тени). 9. Поверхностью вращения общего вида называют поверхность, которая образуется произвольной кривой (плоской или пространственной) при ее вращении вокруг неподвижной оси. В состав определителя поверхности вращения входит образующая g, ось вращения i и условие о том, что эта образующая вращается вокруг оси i: Каждая точка образующей (А, В, С, D, Е) при вращении вокруг оси i описывает окружность с центром на оси вращения. Эти окружности называют параллелями. Наибольшую и наименьшую параллель называют соответственно экватором и горлом (шейкой). Плоскости а, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, — меридианами. Поверхности вращения обладают некоторыми важными свойствами, использующими в процессе конструирования деталей различных машин и механизмов. Например, свойством сдвигаемости, состоящим в том, что поверхность вращения может, вращаясь вокруг оси, сдвигаться без деформации вдоль самой себя. Меридиан поверхности вращения является кратчайшей (или геодезической) линией поверхности. Параллели и меридианы, пересекаясь под прямыми углами, образуют ортогональную сеть на поверхности вращения, аналогично прямоугольной декартовой сети на плоскости. 10. Плоскость проходящую через ось i называютмеридиальной, а линии по которым эта плоскость пересекает поверхность называютсямеридианом. Меридиан, расположенный в плоскости , параллельной плоскости проекций, называется главным меридианом q. Главный меридиан q делит поверхность на две части: видимую и невидимую относительно той плоскости, которой параллельна плоскость главного меридиана. Поверхности вращения – это поверхности созданные при вращении образующей mвокруг оси i. Геометрическая часть определителя состоит из двух линий: образующей m и оси i. Алгоритмическая часть включает две операции: 1. На образующей mвыделяют ряд точек A, B, C,…F; 2. Каждую точку вращают вокруг оси i. Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.
11. Поверхности вращения, образованные прямой линией Вращением прямой линии можно получить следующие виды поверхностей вращения:
Рис.10.2
Рис.10.3
Рис.10.4 Поверхность имеет две образующие линии l(ВС) и l'(В'С'), наклоненные в разные стороны. Эти образующие пересекаются между собой. Точка их пересечения лежит на наименьшей параллели (в данном случае в точке А). Отрезок ОА является кратчайшим расстоянием между образующей и осью. Таким образом, на поверхности однополостного гиперболоида располагаются два семейства прямолинейных образующих. Все образующие одного семейства - скрещивающиеся прямые. Каждая образующая одного семейства пересекает все образующие другого. Через каждую точку поверхности проходят две образующие разных семейств. Меридианом поверхности является гипербола. Рассмотренные поверхности вращения можно отнести и к классу линейчатых поверхностей, так как они образованы в процессе движения прямой линии. Кроме того, поверхности являются поверхностями второго порядка: максимальное число точек пересечения каждой из этих поверхностей с прямой общего положения равно двум. Построение точки на таких поверхностях можно выполнить при помощи параллели или при помощи прямолинейной образующей. |
||||
|
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 201. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
Спроектируем точку А на новую плоскость П4, получим новую проекцию A4точки А. Рассматривая изображение на (фиг.257,а), замечаем, что расстояние от новой проекции A4 до новой оси s14 равно расстоянию от старой проекции A2 до старой оси х12 (A4A14 = А2A12), т.е. отрезок zA4 = zA2
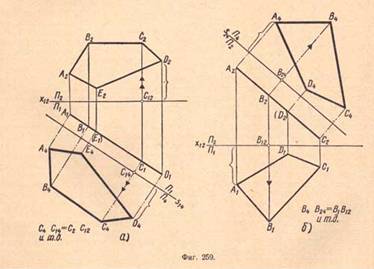На (фиг.259,а) для этой цели плоскость П2 заменена плоскостью П4, параллельной данной фигуре; на плоскости П4 проекция А4В4С4D4E4определяет форму и размеры плоского пятиугольника.
= X(t)
– параметры образующей, а направляющие линии задаются графически, в виде графиков изменения параметров 
в зависимости от значения третьей координаты z (рис.9.4). Тогда при необходимости получения положения некоторой образующей для 
определяют сначала значения параметров 
, которые затем подставляются в уравнение образующей. Кинематический способ образования поверхности связан с понятием определителя поверхности, которым называют совокупность независимых условий, однозначно задающих поверхность. 
Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом. Гиперболоид вращения– различают одно и двух полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.
