
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Предел функции в точке и в бесконечности1. Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {xn}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n хn ≠ а, последовательность {yn = f(xn)} сходится к b. Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму. Указанный предел обозначается так:
Предел функции на бесконечности.Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:
Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:
| |||
Основные теоремы о пределах

  



| Замеча́тельныепреде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела.
Первый замечательный предел:
 Следствия
Следствия


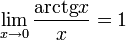
 Второй замечательный предел:
Второй замечательный предел:
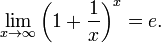 Следствия
Следствия




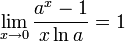 для для  , , 
 Логарифм по основанию e называетсянатуральным логарифмом. Натуральный логарифм числа x обозначается ln x.
Логарифм по основанию e называетсянатуральным логарифмом. Натуральный логарифм числа x обозначается ln x.
| |||
функция f(x) называется непрерывной в точке х0, если
1. Она определена в точке х0
2. Существует конечный предел
 3. Этот предел равен значению функции в точке х0.
Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
3. Этот предел равен значению функции в точке х0.
Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
 Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
 Такая точка называется точкой устранимого разрыва.
Такая точка называется точкой устранимого разрыва.
 Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
| производная функции  -это функция, которая отвечает за ее (функции -это функция, которая отвечает за ее (функции  ) возрастание и убывание.
1) Физический смыслпроизводной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная ) возрастание и убывание.
1) Физический смыслпроизводной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная  – скорость изменения переменной y относительно переменной x в точке – скорость изменения переменной y относительно переменной x в точке  . Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная . Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная  – скорость в момент времени – скорость в момент времени  . Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то . Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то 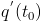 – скорость изменения количества электричества в момент времени – скорость изменения количества электричества в момент времени  , т.е. сила тока в момент времени , т.е. сила тока в момент времени  .
2) Геометрический смысл производной.
Пусть .
2) Геометрический смысл производной.
Пусть  – некоторая кривая, – некоторая кривая,  – точка на кривой – точка на кривой  .
Любая прямая, пересекающая .
Любая прямая, пересекающая  не менее чем в двух точках называется секущей.
Касательной к кривой не менее чем в двух точках называется секущей.
Касательной к кривой  в точке в точке  называется предельное положение секущей называется предельное положение секущей  , если точка , если точка 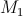 стремится к стремится к  , двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке , двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке  существует, то она единственная
Производной функции существует, то она единственная
Производной функции  в точке в точке  называется величина называется величина 
| |||
Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения  существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
Доказательство. Если существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
Доказательство. Если  , то , то
 ,
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
Рассмотрим на рисунке точки а, b, c.
В точке a при Δx→0 отнош ,
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
Рассмотрим на рисунке точки а, b, c.
В точке a при Δx→0 отнош  ение ение  не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точкеA графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.
В точке b при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точкеA графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.
В точке b при Δx→0 отношение  является знакопостоянной бесконечно большой величиной является знакопостоянной бесконечно большой величиной  . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки. . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
| Пусть функции u = u(x) и v = v(x) имеют производные в точке x0. Тогда в этой точке имеют производные их сумма, произведение и, при дополнительном условии v(x0) ≠ 0, их частное, причем:
|
|||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 196. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 и правосторонний предел
и правосторонний предел  ;
;