
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление обратной матрицы методом ГауссаСтр 1 из 3Следующая ⇒ Из определения обратной матрицы A · A − 1 = E следует, что для вычисления матрицы, обратной квадратной матрице n –го порядка A , нужно решить матричное уравнение
где X — неизвестная обратная матрица. Это матричное уравнение эквивалентно n системам n линейных уравнений n–го порядка с одной и той же основной матрицей системыA , но разными столбцами свободных членов, а именно, столбцами единичной матрицы. Поэтому решать все эти системы методом Гаусса удобно одновременно. Таким образом, для вычисления обратной матрицы методом Гаусса 1. Дописываем единичную матрицу E к матрице A (для удобства отделяя ее чертой). 2. С помощью элементарных преобразований строк преобразуем матрицу A к единичной. Тогда на месте единичной матрицы окажется искомая обратная матрица:
Если матрица A не может быть приведена к единичной, то это означает, что она вырожденная и, следовательно, не имеет обратной (следовательно, можно не проверять заранее, что det A ≠ 0 ).
| 
| ||||
Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы Dсистемы матрицу A системы приводят к ступенчатому виду:

 Если среди чисел Если среди чисел  есть отличные от нуля, система несовместна.
Если есть отличные от нуля, система несовместна.
Если  то:
1) при r = n исходная система равносильна системе: то:
1) при r = n исходная система равносильна системе:
 имеющей единственное решение (сначала находим из последнего уравнения
имеющей единственное решение (сначала находим из последнего уравнения  , из предпоследнего , из предпоследнего  . .
| Общее уравнение прямой
Ах+Ву+С=0
(где А, В, С могут иметь любые значения, лишь бы коэффициенты А, В не были нулями оба сразу) представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.
Если А=0, то есть уравнение не содержит х, то оно представляет прямую, параллельную оси ОХ.
Если В=0, то есть уравнение не содержит у, то оно представляет прямую, параллельную оси ОY.
Когла В не равно нулю, то общее уравнение прямой можно разрешить относительно ординаты у, тогда оно преобразуется к виду
y=ax+b
(где a=-A/B; b=-C/B).
Аналогично, при А отличным от нуля общее уравнение прямой можно разрешить относительно х.
Если С=0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат.
Уравнение прямой с угловым коэффициентом
Если в общем уравнении прямой  , то его можно записать в виде уравнения с угловым коэффициентом , то его можно записать в виде уравнения с угловым коэффициентом
 где
где 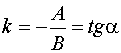 угловой коэффициент,
a – угол, образованный прямой с положительным направлением оси угловой коэффициент,
a – угол, образованный прямой с положительным направлением оси  , , 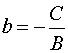 – свободный член, равный ординате точки пересечения прямой с осью – свободный член, равный ординате точки пересечения прямой с осью  .
Однозначно определить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку .
Однозначно определить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку  с угловым коэффициентом с угловым коэффициентом  , определяется по формуле , определяется по формуле
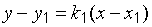 . .
| |||||
Уравнение прямой, проходящей через две заданные точки
В соответствии с условием, нам известны координаты двух точек  и и  . Данная задача сформулирована корректно, так как известно, что через две точки проходит одна и только одна прямая линия. . Данная задача сформулирована корректно, так как известно, что через две точки проходит одна и только одна прямая линия.
 Рисунок 1.4. Прямая, проходящая через две заданных точки
Если учесть, что уравнение (1-7) прямой проходящей через заданную точку
Рисунок 1.4. Прямая, проходящая через две заданных точки
Если учесть, что уравнение (1-7) прямой проходящей через заданную точку  в заданном направлении, определяет все прямые, проходящие через точку в заданном направлении, определяет все прямые, проходящие через точку  . Из них, нужно выбрать одну, которая будет проходить и через точку . Из них, нужно выбрать одну, которая будет проходить и через точку  . Для этого нужно определить конкретное значение углового коэффициента K искомой прямой. Его значение можно определить, если в (1-7) подставить координаты точки . Для этого нужно определить конкретное значение углового коэффициента K искомой прямой. Его значение можно определить, если в (1-7) подставить координаты точки  , которая принадлежит искомой прямой , которая принадлежит искомой прямой
 ,
И искомое значение k равно ,
И искомое значение k равно
 .
Подставим найденное значение углового коэффициента K в уравнение (1-7). После преобразований получим: .
Подставим найденное значение углового коэффициента K в уравнение (1-7). После преобразований получим:
 (1-8)
Это и есть уравнение искомой прямой, проходящей через две заданные точки.
Кривые второго порядка.
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае Ах2 + 2Вху +Су2 + 2Дх + 2Еу +F = 0,
где А, В, С, Д, Е, F – действительные числа и по крайней мере одно из чисел А2+В2+С2≠0.
Окружность
Центр окружности – это геометрическое место точек в плоскости равностоящих от точки плоскости С(а,b).
Окружность задается следующим уравнением: (1-8)
Это и есть уравнение искомой прямой, проходящей через две заданные точки.
Кривые второго порядка.
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае Ах2 + 2Вху +Су2 + 2Дх + 2Еу +F = 0,
где А, В, С, Д, Е, F – действительные числа и по крайней мере одно из чисел А2+В2+С2≠0.
Окружность
Центр окружности – это геометрическое место точек в плоскости равностоящих от точки плоскости С(а,b).
Окружность задается следующим уравнением:
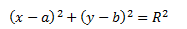 Где х,у – координаты произвольной точки окружности, R - радиус окружности.
Признак уравнения окружности
1. Отсутствует слагаемое с х,у
2. Равны Коэффициенты при х2 и у2
Эллипс
Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами (постоянная величина).
Каноническое уравнение эллипса:
Где х,у – координаты произвольной точки окружности, R - радиус окружности.
Признак уравнения окружности
1. Отсутствует слагаемое с х,у
2. Равны Коэффициенты при х2 и у2
Эллипс
Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами (постоянная величина).
Каноническое уравнение эллипса:
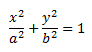 Х и у принадлежат эллипсу.
а – большая полуось эллипса
b – малая полуось эллипса
У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса.
Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.
Если центры эллипса находятся не в центре С(α, β)
Х и у принадлежат эллипсу.
а – большая полуось эллипса
b – малая полуось эллипса
У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса.
Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.
Если центры эллипса находятся не в центре С(α, β)
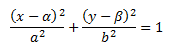 Гипербола
Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.
Каноническое уравнение гиперболы Гипербола
Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.
Каноническое уравнение гиперболы
 Гипербола имеет 2 оси симметрии:
а – действительная полуось симметрии
b – мнимая полуось симметрии
Ассимптоты гиперболы:
Гипербола имеет 2 оси симметрии:
а – действительная полуось симметрии
b – мнимая полуось симметрии
Ассимптоты гиперболы:
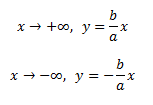 Парабола
Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.
Каноническое уравнение параболы:
У2=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)
Если вершина параболы С (α, β), то уравнение параболы (у-β)2=2р(х-α)
Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х2=2qу
Бесконечно малые и бесконечно большие функции
Важную роль в математическом анализе играет понятие бесконечно малых (б.м.) функций.
О: Функция у = а(х) называется б.м. при х Парабола
Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.
Каноническое уравнение параболы:
У2=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)
Если вершина параболы С (α, β), то уравнение параболы (у-β)2=2р(х-α)
Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х2=2qу
Бесконечно малые и бесконечно большие функции
Важную роль в математическом анализе играет понятие бесконечно малых (б.м.) функций.
О: Функция у = а(х) называется б.м. при х  а, если а, если
 Функция
Функция  называется б.б. при называется б.б. при 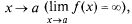 если для любого числа М > 0 существует такое число
если для любого числа М > 0 существует такое число 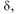 зависящее только от М, что из неравенства зависящее только от М, что из неравенства 
|
При А  0, В 0, В  0 и С 0 и С  0 получаем уравнение прямой в отрезках на осях: 0 получаем уравнение прямой в отрезках на осях:
 где a = – C / A , b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной a и b .
Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
1). Пусть прямые L1 и L2 заданы общими уравнениями
где a = – C / A , b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной a и b .
Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
1). Пусть прямые L1 и L2 заданы общими уравнениями
 .
Задача об определении угла между прямыми сводится к определению угла между нормальными векторами .
Задача об определении угла между прямыми сводится к определению угла между нормальными векторами 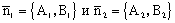 этих прямых: этих прямых:
 (6.6)
Условие параллельности прямых L1 и L2 эквивалентно коллинеарности их нормальных векторов (6.6)
Условие параллельности прямых L1 и L2 эквивалентно коллинеарности их нормальных векторов 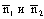 : :
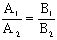 .
Условие перпендикулярности прямых L1 и L2 получаем из формулы (6.6) при
cos .
Условие перпендикулярности прямых L1 и L2 получаем из формулы (6.6) при
cos  = 0: = 0:
 .
2). Если прямые L1 и L2 заданы каноническими уравнениями .
2). Если прямые L1 и L2 заданы каноническими уравнениями
 ,
то рассматривая их направляющие векторы ,
то рассматривая их направляющие векторы  , аналогично случаю 1).имеем: , аналогично случаю 1).имеем:
 (6.7)
Условие параллельности прямых L1 и L2 : (6.7)
Условие параллельности прямых L1 и L2 :
 .
Условие перпендикулярности прямых L1 и L2 : .
Условие перпендикулярности прямых L1 и L2 :
 3). Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
3). Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом  . .
Отсюда 
Т.е. угол между прямыми L1 и L2 определяется по формуле:
Если в этой формуле поменять местами k1 и k2 , то формула определит нам угол между прямыми, смежный к прежнему углу. Т.к. эти два угла в сумме равны Прямые параллельны, если tg Условие перпендикулярности прямых L1 и L2 получим из формулы (6.8), т.к. tg Условие перпендикулярности прямых L1 и L2 запишем в виде:
|
|||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 206. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 - углы наклона прямых L1 и L2 к оси Ox, а
- углы наклона прямых L1 и L2 к оси Ox, а 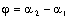 .
.
 .
. (6.8)
(6.8) и их тангенсы отличаются только знаком.
и их тангенсы отличаются только знаком. .
.