Данные для нахождения коэффициента корреляции

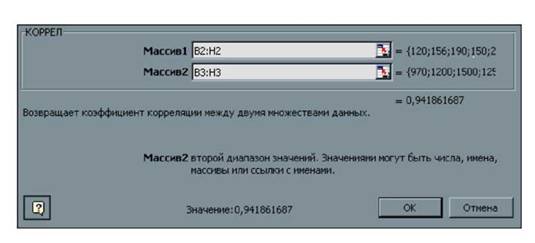
Таблица 16

1. В окне мастера функций (рис.7) в левом поле «категория» выбира­ем категорию «статистическая». В правом поле соответственно отразятся все статистические функции.

2. Находим и выбираем в правом поле функцию КОРРЕЛ и нажимаем ОК.

3. В поле Массив 1 вносим координаты первого динамического ряда, который отражает динамику количества преступлений. В нашем примере это - В2:Н2. (рис. 7).

4. В поле Массив 2 вносим координаты второго динамического ряда, который отражает динамику количества безработных. В нашем примере это - ВЗ:НЗ (рис.7).

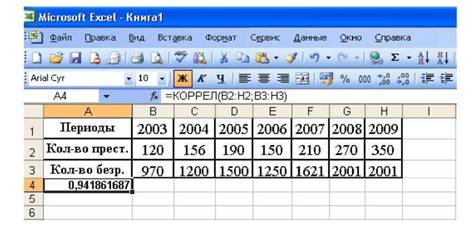
Рис. 7. Окноf_xдля внесения координат динамических рядов

9. Нажимаем ОК. В ячейке, где вы установили курсор, должно поя­виться число 0,941862, отражающее силу взаимосвязи между явлениями (рис. 8).

Рис.8. Окно программы Excel с результатами расчета коэффициента корреляции

В соответствии с предложенной выше классификацией коэффициен­тов парной корреляции теснота взаимосвязи между динамикой количества безработных и динамикой количества преступлений относится к категории очень сильной взаимосвязи. Такой вывод позволяет в дальнейшем уверен­но подбирать математическую модель этой зависимости для целей прогно­зирования.

Регрессионный анализ

Понятия корреляции и регрессии непосредственно связаны между собой. В корреляционном и регрессионном анализе много общих вы­числительных приемов. Они используются для выявления причинно- следственных соотношений между явлениями и процессами. Однако, если корреляционный анализ позволяет оценить силу и направление стохастической связи, то регрессионный анализ - еще и функцию зави­симости. При этом следует отметить, что чем слабее взаимосвязь, тем больше диаграмма рассеяния похожа на облако (рис.5) и тем труднее определить функцию зависимости.

Регрессия может быть:

а) в зависимости от числа явлений (переменных):

· простой (регрессия между двумя переменными);

· множественной (регрессия между зависимой переменной (у) и несколькими объясняющими ее переменными (х₁ х₂...х_n );

б) в зависимости от формы:

· линейной (отображается линейной функцией, а между изучаемыми переменными существуют линейные соотношения (рис. 4, рис. 9));