Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Количество преступлений по кварталам
Таблица 13
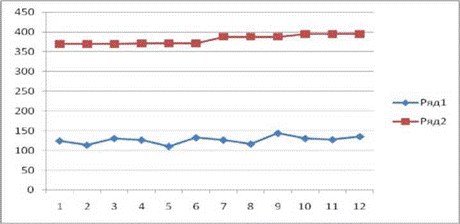
Графическая интерпретация исходного (ряд I) и преобразованного динамического ряда (ряд 2) показывает, что последний имеет более ровный, отражающий тенденцию развития вид (рис 1).
Рис.1. Выравнивание динамического ряда методом укрупненных интервалов
Для выравнивания динамических рядов используется и метод скользящей средней величины. Его суть заключается в замене фактических показателей уровней ряда скользящими средними величинами, взятыми в пределах последовательно скользящего интервала. При этом методе по каждому выбранному укрупненному интервалу берется средняя арифметическая фактических уровней, а интервал, начиная с первого, каждый раз переносится на один «шаг» вправо. Рассмотрим использование метода скользящей средней для выравнивания динамического ряда коэффициента интенсивности (уровня) разбоев по отдельному региону на 100 тыс. населения (см. табл. 15).
Динамика уровня разбоев по региону
Таблица 15
Сдвигаем интервал на один «шаг» и вычисляем среднюю арифметическую для следующих трех месяцев:
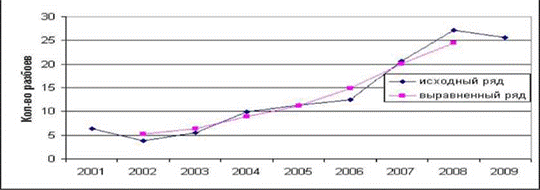
В результате последующих аналогичных вычислений получаем выровненный ряд: 5,2; 6,4; 8,9; 11,2; 14,8; 20,1; 24,5 (см. строку "Выровненный ряд" в табл. 12).  На рис.2 представлена графическая интерпретация выравнивания динамического ряда методов скользящей средней.
Рис. 2. Выравнивание динамического ряда методом скользящей средней
Как отмечено выше, аналитические методы выравнивания динамических рядов дают более четкое представление о тенденциях изменения анализируемого явления. Наиболее известным среди аналитических методов выравнивания является метод наименьших квадратов (рис. 1). Сущность этого метода заключается в построении на основе фактических данных динамического ряда (исходный ряд), взятых из таблицы 15, теоретической кривой таким образом, чтобы сумма квадратов расстояний между точками этих кривых была минимальной.
Рис. 3. Выравнивание динамического ряда аналитическим методом
Полученная расчетная кривая отражает длительную тенденцию изменения каких-либо показателей, носит название тренда (англ. trend - тенденция) и является основой для дальнейшего прогнозирования изучаемого явления. В данном случае на рис.З приведен вариант построения тренда на основе полиномиальной модели.
3. ВЫЯВЛЕНИЕ ВЗАИМОСВЯЗЕЙ В СОЦИАЛЬНО-ПРАВОВЫХ ПРОЦЕССАХ
Разработка тренда, отражающего тенденцию развития какого-либо социально-правового явления, есть база для разработки прогноза. Но прогнозирование как бы «само из себя» без учета влияния внешних факторов может привести к достаточно серьезной ошибке. Особенно это касается нестабильных систем, где причинно-следственные зависимости быстро меняются не только по форме и силе, но иногда и по направлению. Поэтому необходимо идти от исследования преступности в ее "чистом" виде к исследованию тех явлений, процессов и факторов, которые влияют на нее. Главным вопросом при этом выступает не только определение и изучение таких факторов, но и расчет силы их влияния на преступность. Для исследования зависимостей между анализируемыми признаками обычно используют методы корреляционного и регрессионного анализов. Корреляционный анализ Между социально-правовыми явлениями и процессами возможны два вида зависимости: функциональная и стохастическая. При функциональной зависимости имеется однозначное соответствие тех или иных параметров, характеризующих различные явления. Примеры такого рода зависимостей в социально-правовой среде практически не встречаются. При стохастической (вероятностной) зависимости конкретному значению зависимой переменной соответствует набор значений независимой переменной. Это связано, прежде всего, с тем, что на зависимую переменную оказывает влияние ряд неучтенных факторов. Кроме того, сказываются ошибки измерения переменных: вследствие случайного разброса их значения могут быть указаны лишь с определенной вероятностью. В социально-правовой сфере приходится сталкиваться со многими явлениями, имеющими вероятностную природу. Так, число совершенных и раскрытых преступлений за фиксированный отрезок времени, число дорожно-транспортных происшествий в каком-либо регионе за определенное время - все это случайные величины. Для изучения стохастических взаимосвязей существуют специальные методы, в частности, корреляционный анализ («корреляция» - соотношение, связь между имеющимися явлениями и процессами). Корреляционный анализ - это использование в определенной последовательности совокупности статистических методов обработки информации, позволяющее исследовать взаимосвязи между различными переменными. Задачей корреляционного анализа как метода математической статистики является установление формы и направления связи, а также измерение тесноты этой связи между изучаемыми случайными переменными (например, между преступностью и количеством проживающего в этом районе населения). В статистике величина линейной зависимости между двумя признаками часто измеряется посредством простого (выборочного) коэффициента корреляции. Величина линейной зависимости одной переменной от нескольких других измеряется коэффициентом множественной корреляции. Возможно вычисление частного коэффициента корреляции, который измеряет линейную зависимость между двумя переменными после устранения части линейной зависимости, обусловленной связью этих переменных с другими. По форме корреляционные связи могут быть линейными и нелинейными (см. соответственно рис. 4 и рис. 10), а по направлению - прямыми (положительными) и обратными (отрицательными). Прямая связь свидетельствует о том, что с увеличением (уменьшением) значений одной переменной увеличиваются (уменьшаются) значения другой переменной. При обратной связи увеличение (уменьшение) значений одной переменной ведет к уменьшению (увеличению) значений другой переменной. Главная задача корреляционного анализа - измерение тесноты связи решается путем вычисления различных коэффициентов корреляции и проверки их значимости. Коэффициент корреляции может принимать значения при прямой связи от 0 до +1, а при обратной - от -1 до 0. При коэффициентах, близких к 0, считается, что статистическая линейная связь между признаками отсутствует; при абсолютных значениях коэффициентов, меньших 0,3, - связь слабая; при значениях 0,3...0,5 - связь умеренная; при 0,5...0,7 - связь значительная; при 0,7...0,9 - связь сильная; если значения коэффициентов больше 0,9, то связь считается очень сильной; если коэффициенты равны + 1 или -1, то говорится о функциональной связи (что практически не встречается в статистических исследованиях). Для определения существования и величины линейной зависимости между двумя переменными X и У необходимо осуществить две процедуры. Первая процедура заключается в графическом отображении точек Xi,Yi, (i=l,...,n) на плоскость XY. Полученный график (рис.4, 5) называется диаграммой рассеяния, анализ которой позволяет сделать вывод о допустимости предположения о линейной зависимости между переменными. Если такое предположение допустимо, то необходимо выразить в количественном виде величину линейной связи. Для этого используется выборочный коэффициент корреляции.
Рис. 4. Линейная зависимость Рис. 5. Линейная зависимость определена не определена
В то же время отсутствие статистически значимой связи не говорит об отсутствии причинно-следственных отношений, а заставляет искать другие пути и средства ее выявления, если содержательная концепция и практический опыт указывают на ее возможное существование. Вторая процедура заключается в непосредственном расчете величины коэффициента корреляции по специальным математическим формулам. Сложность и громоздкость математической процедуры расчета не позволяет привести ее в кратком изложении в данной лекции, поэтому рассмотрим простой вариант нахождения коэффициента парной корреляции при помощи программы Excel. Пример 1 Используя электронную таблицу Excel, определить значение коэффициента корреляции между двумя явлениями - преступность и безработица, представленными динамическими рядами за семилетний период (табл. 16). 1. Открыть программу Excel. 2. Ввести данные из таблицы 16. 3. Установить курсор в свободную ячейку, например в А4. В ней в дальнейшем отразится результат нашего расчета. 4. В панели инструментов включаем кнопку «Мастер функций»(fx).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 233. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
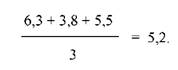 Допустим, принимаем укрупненный интервал в три года и в его пределах вычисляем среднюю арифметическую уровней:
Допустим, принимаем укрупненный интервал в три года и в его пределах вычисляем среднюю арифметическую уровней: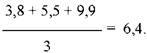

 Однако даже при наличии сильной статистически значимой связи между двумя переменными нельзя быть полностью уверенным в их причинно-следственной обусловленности, так как могут существовать другие причины (факторы), определяющие их совместную статистическую взаимосвязь. Статистические выводы должны быть всегда обоснованы надежной теоретической концепцией, логически понятны, подтверждаться практикой.
Однако даже при наличии сильной статистически значимой связи между двумя переменными нельзя быть полностью уверенным в их причинно-следственной обусловленности, так как могут существовать другие причины (факторы), определяющие их совместную статистическую взаимосвязь. Статистические выводы должны быть всегда обоснованы надежной теоретической концепцией, логически понятны, подтверждаться практикой.