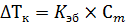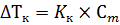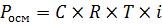Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Способ решения через уравнение.В 200 граммах итогового (третьего) раствора должно оказаться 50 г вещества:
За Х можно обозначить массу одного из растворов, тогда масса второго раствора равна 200 – Х, а массы вещества в первом (X*W1(Х)) и втором ((200-X)*W2(Х)) вместе должны быть равны 50 граммам:
Решение этого уравнения даёт результат. Х = 100 гр. Следовательно, нужно взять по 100 грамм первого и второго растворов. Однако, далеко не всегда попадаются такие удобные концентрации, поэтому результат вычисления зависит от способа решения и составления уравнения. Если за Х обозначить не массу раствора, а массу вещества в одном из растворов, результат будет немного другим. Это и есть недостаток первого способа решения такой задачи. Правило креста Решение такой задачи по правилу креста выглядит так: 1) В столбик записываются концентрации исходных растворов. 35%
15% 2) Между ними помещается концентрация того раствора, который требуется приготовить. 35% 25% 15% 3) И затем по диагоналям высчитывается разница между этими числами, без учета знака.
15% 10 4) Верхнее число относится к нижнему так – же, как массы первого и второго растворов.
Отсюда очевидно, что массы исходных растворов равны. Ответ: нужно взять по 100 г исходных растворов.
Вопросы для самоконтроля.
1) Что такое дисперсные системы? Почему на практике приходится иметь дело с ними, а не индивидуальными веществами? 2) Как можно классифицировать дисперсные системы? Какими свойствами обладают истинные и коллоидные растворы? 3) Что такое раствор? Как можно количественно охарактеризовать? 4) Как относятся молярность и нормальность?  5) Какова природа процесса растворения? Что является его движущей силой? 6) Какие виды растворов, и по каким критериям можно выделить? 7) Что такое растворимость вещества? 8) Как можно отличить растворенное вещество от растворителя?
Задания для самоконтроля
1) Для приготовления некоторого маринада хозяйке требуется 10 гр 5%(масс) уксусного раствора. Продающаяся в магазинах эссенция содержит 70%(масс) уксусной кислоты. Какие массы воды и эссенции нужно смешать хозяйке? Ответ: 0,7 г эссенции и 9,3 г воды 2) Какое количество вещества соляной кислоты (HCl) содержится в 600 г 35%(масс) раствора? Ответ: 5,75 моль.
6.2 Коллигативные свойства растворов
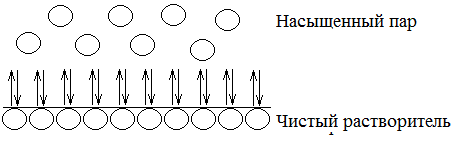
Раствор, вне зависимости от его типа, обладает рядом свойств, которые напрямую вытекают из законов термодинамики. Следовательно, природа частиц, находящихся в растворе, на эти свойства не оказывает никакого влияния, эти свойства зависят только от количества частиц дисперсной фазы. Эти свойства называются коллигативными. Над раствором присутствуют пары растворителя, которые образуют газовую фазу. Испарение молекул растворителя в газовую фазу и их конденсация на поверхности жидкости формируют термодинамическое равновесие «испарение – конденсация», раз этот процесс равновесный, то, по определению, ΔG этого процесса равна 0. Но как только происходит изменение концентрации растворенного вещества – происходит отклонение энергии Гиббса от 0, и равновесие между этими двумя процессами смещается. Это происходит по двум причинам: · Во-первых, при увеличении концентрации растворенного вещества, количество его частиц увеличится и на поверхности раствора, следовательно, уменьшится площадь, с которой происходит испарение молекул растворителя. · Во-вторых, мало того, что частицы растворенного вещества занимают «места», с которых происходит испарение растворителя, они образуют вокруг себя сольватную оболочку, прочно связывая в нее молекулы растворителя. То есть, растворенное вещество не только занимает часть поверхности раствора, но еще и мешает испаряться соседним молекулам. Это приводит к тому, что при повышении концентрации раствора давление паров растворителя над ним уменьшается (рисунок 6.1). Количественно это явление описывается первым законом Рауля: относительно понижение давления пара над растворителем равно молярной доли растворенного вещества:
где P – давление насыщенного пара над раствором, P0 - давление насыщенного пара над чистым растворителем при данной температуре, N – мольная доля вещества в растворе. Рисунок 6.1. Влияние растворенного вещества на равновесие между насыщенным паром и жидкостью. Белым цветом указан растворитель, черным – растворенное вещество, серым – растворитель в сольватной оболочке. Если раствор состоит только из двух веществ – растворителя и растворенного вещества, то первый закон Рауля можно трансформировать для расчета давления насыщенного пара по мольной доле растворителя:
Итак, у любого раствора, по сравнению с чистым растворителем падает давление насыщенного пара над его поверхностью. К чему еще это может привести? Вспомним, что такое температура кипения – это температура, при которой давление насыщенного пара равно атмосферному. И раз давление насыщенного пара раствора падает, то для запуска процесса кипения потребуется большая температура. У растворов температура кипения выше, чем у чистого растворителя. Однако, и это еще не все. От давления насыщенного пара зависит и температура кристаллизации, о чем более детально рассказывается в курсе физической химии. Эти изменения температур кипения и кристаллизации описываются вторым законом Рауля: изменение температур кипения и замерзания прямопропорциональны моляльности раствора:
где ΔTкр и ΔTкип – изменение температур кристаллизации и кипения раствора, Kкр и Kэ – криоскопическая и эбуллиоскопическая константы, которые показываю, как изменится температура кристаллизации и температура кипения раствора соответственно, при концентрации растворенного вещества 1 моль/кг. Для воды криоскопическая константа равна 1,86°С, а эбуллиоскопическая 0,52°С. Последнее явление, которое будет рассмотрено в этой главе – осмос. Осмос возникает в том случае, если два раствора с разной концентрацией разделены между собой полупроницаемой мембраной, такой, через которую может проникнуть молекула растворителя, но не может пройти молекула растворенного вещества. При выполнении этих условий начинается осмотическое движение молекул растворителя через мембрану, из раствора с низкой концентрацией в раствор с высокой концентрацией (рисунок 6.2).
Рисунок 6.2. Осмос в U-образной трубке Это приводит к тому, что концентрация разбавленного раствора будет увеличиваться, а концентрированного уменьшаться. Осмос прекращается, когда в этих двух растворах выравниваются концентрации. Таким образом, осмос – это явление движения частиц растворителя через полупроницаемую перегородку из раствора с меньшей концентрацией в раствор большей концентрацией. Это явление имеет большое значение в биологических процессах, так как клеточная оболочка как раз является подобной полупроницаемой мембраной. Например, студентам биологических специальностей известно явление плазмолиза. Под воздействием концентрированного раствора соли из цитоплазмы клеток во внешнюю среду будет вытягиваться вода. В конечном итоге это приводит к гибели клетки. Поэтому мёд и соляные рассолы широко использовались для консервации пищи. Гнилостные бактерии погибают из-за плазмолиза, попадая в рассол или мед. В качестве другого примера можно взять опыт, известный каждому школьнику – набухание семян растений в воде. Причем, интенсивность этого процесса довольно велика. Известен случай, когда разбухание груза семян в трюме корабля привело к деформации его стальных поперечных переборок (пароход «Харьков», 1933) [38]. Количественно осмос можно оценить с помощью такой величины, как осмотическое давление. Осмотическое давление – это давление, которое необходимо приложить к системе[4], что бы осмос прекратился. Величину осмотического давления можно рассчитать по закону Вант-Гоффа:
где Pосм – осмотическое давление, кПа, C – молярная концентрация, моль/л, T –температура, К, R – универсальная газовая постоянная. Молярную концентрацию можно представить в виде
Отсюда видно, что зная осмотическое давление раствора, можно рассчитать молярную массу растворенного вещества. Если приложенное к системе давление будет больше осмотического, то направление осмоса поменяется. Явление обратного осмоса используется в осмотических опреснителях.
Пример решения задачи на тему «Коллигативные свойства».
Задача: Рассчитать давление пара над раствором (P), температуры замерзания и кипения (Tз и Тк) и осмотическое давление (Pосм) 20%(масс) водного раствора ацетона (C3H6O). Плотность раствора 0,969 г/мл, температура 250С. Решение: 1) Давление пара над раствором определяется по первому закону Рауля.
P0 – давление пара над чистым растворителем при заданной температуре. Для воды P0 при 250С составляет 3,17кПа. Осталось рассчитать мольную долю ацетона: Количество вещества ацетона можно вычислить, поделив его массу на молярную массу. Масса ацетона равна произведению его массовой доли на массу раствора. Масса раствора высчитывается как произведение объема на плотность. Объема в условиях задачи нет. В таком случае берется любое удобное число для расчетов, проще всего взять 1 литр, отсюда: m(р-ра)=V×ρ=1000 мл×0,969 г/мл = 969 г m(C3H6O)= m(р-ра) ×W(C3H6O) = 969 г×20% =193,8 г
Аналогично рассчитывается количество вещества воды. Раз раствор состоит всего из двух веществ, значит, масса воды равна разности масс раствора и ацетона = 969 г – 193,8 г = 775,2 г. Количество вещества воды высчитывается как соотношение массы и молярной массы: n(H2O) = Итак, 2) Температуры кипения и замерзания рассчитываются по второму закону Рауля:
ΔT – изменение температур кипения и замерзания раствора, по сравнению с водой, K – эбуллиоскопическая и криоскопическая константы, для воды они равны 0,520и 1,860С соответственно, Cm – моляльность.
Следовательно, этот раствор кипит при температуре 102,240С, а замерзает при -8,020С. 3) Осмотическое давление рассчитывается по уравнению Вант-Гоффа:
где C – молярная концентрация вещества, R – универсальная газовая постоянная (8,31 Дж/моль*К), Т – температура, К.
T = Т, 0С+273=298 К Отсюда Ответ: P =2,94 кПа, Тк = 102,240С, Тз = -8,020С, Pосм = 8271 кПа.
Вопросы и задания для самоконтроля
1) Что такое коллигативные свойства? 2) От чего зависит их величина? 3) Какие процессы, кроме перечисленных выше, зависят от осмоса? 4) Некоторый раствор неэлектролита содержит 0,1 моль вещества в 100 г воды. Чему равна температура замерзания этого раствора? Ответ: -1,860С 5) Мольная доля неэлектролита в водном растворе 0,1. Чему равно давление насыщенного пара над этим раствором при 250С? Ответ: 2,9 кПа. 6) Почему при вводе в кровь человека раствора глюкозы (C6H12O6) его концентрация должна быть 5% (масс)?
6.3 Растворы электролитов. Электролитическая диссоциация.
Исходя из того, что коллигативные свойства являются следствием законов термодинамики, можно было – бы предположить, что формулы законов Рауля и Вант-Гоффа работают для всех растворов, но это не так. В некоторых случаях наблюдались сильные отклонения от этих законов, в сторону увеличения. Сам Вант-Гофф в 1887 году вел в своё уравнение поправку – изотонический коэффициент (i), который показывал, во сколько раз экспериментальные ΔTкр, ΔTкип, P насыщенного пара и Pосм больше рассчитанных теоретических:
Или – же, если сравнивать отношение экспериментальных и рассчитанных теоретических величин:
Этот изотонический коэффициент для всех растворов, оказывается больше 1. Так как коллигативные свойства зависят от количества частиц растворенного вещества, то из этих данных следует однозначный вывод о том, что количество частиц растворяемого вещества при растворении увеличивается. Кроме того, растворы, для которых наблюдается это явление, еще и проводят электрический ток. Значит, вещество при растворении не просто распадается на частицы, оно распадается на заряженные частицы – ионы. Классическая теория, которая объясняет это явление, была предложена Аррениусом и Оствальдом в 1887 году. Именно с позиций этой теории рассматривается дальнейший курс неорганической химии в школе, хотя у неё есть ряд недостатков, и в современной химии она не используется. Но так как данное пособие написано для студентов педагогических специальностей, то начать придется с неё. Вот основные положения теории диссоциации Аррениуса: |
|||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 286. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 35% 10
35% 10
 25%
25%






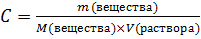 . Тогда закон Вант-Гоффа приобретает вид:
. Тогда закон Вант-Гоффа приобретает вид:


 3,34 моль
3,34 моль = 43,07 моль.
= 43,07 моль. , отсюда
, отсюда 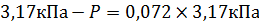 , P =2,94 кПа.
, P =2,94 кПа.