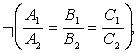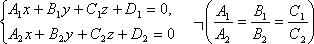Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Взаимное расположение двух плоскостейСтр 1 из 3Следующая ⇒ Афінні простори. Афінні координати. Формули перетворення Афінних координат точок.
2. Площини в афінних просторах. Плоскость
Одномерная плоскость – прямая. Если m = n – 1, то плоскость называется гиперплоскостью.
Если ранг = 1, то плоскости совпадают. Если ранг матрицы = 2, то плоскости пересекаются по прямой. Плоскости называются параллельными, если
Плоскости называются скрещивающимися, если они не параллельны и не имеют общих точек Аксіоми скалярного множення. Евклідові векторні простори. Евклідові точково-векторні простори.
Кут між векторами. Ортогональні вектори. Ортонормовані базиси і прямокутні координати.
5. Векторний та мішаний добутки.
Прямі в афінному прсторі. Паралельні прямі. Відрізки. Просте відношення трьох точок.
Теорія прямих на афінній площині. Способи завдання прямої на афінній площині. Взаємне розташування двох прямих. Жмуток прямих.
Теорія прямих на евклідовій площині. Нормальне рівняння прямої. Відстань від точки до прямої.
9. Еліпс, гіпербола, парабола.
Площини у 3-вимірному афінному просторі Геометричні способи завдання площини. Взаємне розташування двох площин. Жмуток площин.  Плоскость в трехмерном аффинном пространстве 1) векторно параметрическим уравнением Возьмем теперь в пространстве аффинную систему координат Охyz. Пусть в этой системе координат точки и векторы имеют соответствующие координаты 2) общим уравнением
Система уравнения или эквивалентна ее системе Уравнением плоскости, которое проходит через три точки с координатами
Пусть плоскость проходит через точки Прямая линия в пространстве может быть задана: 1) векторно параметрическим уравнением Если уравнение Прямую l можно задать как линию пересечения Взаимное расположение двух плоскостей Если 1) пересекаются 2) параллельны (но не совпадают) 3) совпадают Если плоскости заданы уравнениями 1) 2) 3) Пучок плоскостей Если
есть ось пучка, то уравнение пучка
Существует всего 4 способа задания плоскости
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 281. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




 определенной точкой
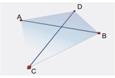
определенной точкой  и двумя неколлинеарными векторами
и двумя неколлинеарными векторами  называется множество точек аффинного пространства
называется множество точек аффинного пространства  такое что
такое что 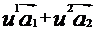 .
.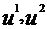 - числа (параметры)
- числа (параметры)


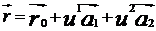 - векторно-параметрическое уравнение плоскости
- векторно-параметрическое уравнение плоскости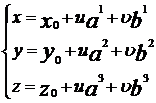

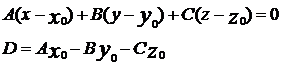
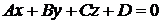 - общее уравнение плоскости
- общее уравнение плоскости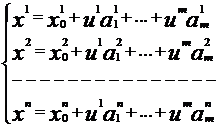 - параметрическое уравнение n-мерной плоскости
- параметрическое уравнение n-мерной плоскости либо
либо 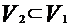
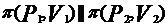 (ранг матрицы =1 ранг расширенной матрицы = 2)
(ранг матрицы =1 ранг расширенной матрицы = 2)















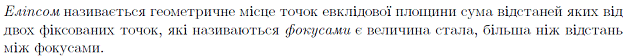


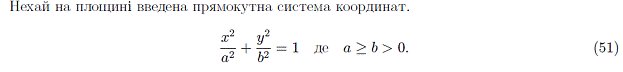




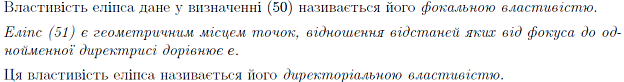










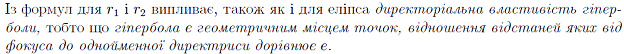
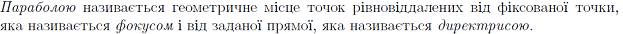






 может быть задана:
может быть задана: , где a, b – неколлинеарные направленные векторы плоскости,
, где a, b – неколлинеарные направленные векторы плоскости,  - радиус-вектор фиксированной точки плоскости.
- радиус-вектор фиксированной точки плоскости.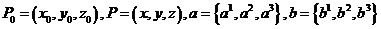 . Тогда в заданной системе координат уравнения
. Тогда в заданной системе координат уравнения  . Эти уравнения называются параметрическими уравнениями плоскости.
. Эти уравнения называются параметрическими уравнениями плоскости.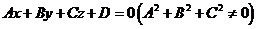 .
. выражает линейную зависимость рядов матрицы
выражает линейную зависимость рядов матрицы  или уравнение
или уравнение  где
где  Уравнение можно назвать общим уравнением плоскости, которая проходит через тоску
Уравнение можно назвать общим уравнением плоскости, которая проходит через тоску  .
. , которое не лежит на одной прямой, можно записать в виде
, которое не лежит на одной прямой, можно записать в виде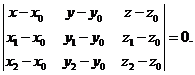
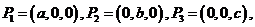 где
где  . Тогда уравнение этой плоскости можно записать в виде
. Тогда уравнение этой плоскости можно записать в виде  . Это уравнение называют уравнением плоскости в отрезках.
. Это уравнение называют уравнением плоскости в отрезках. , где а – направленный вектор прямой,
, где а – направленный вектор прямой,  записать в аффинной системе координат, то получим параметрическое уравнение прямой в пространстве:
записать в аффинной системе координат, то получим параметрическое уравнение прямой в пространстве:  . Включением параметра параметрические уравнения сводится к канонической форме
. Включением параметра параметрические уравнения сводится к канонической форме  . Уравнение прямой, которое проходит через две разные точки, можно задать в векторной форме
. Уравнение прямой, которое проходит через две разные точки, можно задать в векторной форме  , где
, где 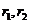 - радиус-вектор данных точек, а
- радиус-вектор данных точек, а  - их аффинные координаты.
- их аффинные координаты. , то они:
, то они:

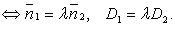
 и
и  то случаи 1 - 3 имеют месло, когда:
то случаи 1 - 3 имеют месло, когда: