
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Процессов II и III типов точностиЕсли на основании графика эмпирической зависимости
Определение погрешности обработки для процесса, относящегося к II типу точности. Определение функциональных и постоянных погрешностей для процессов II типа точности производится следующим образом. Сначала спрямляется кривая изменения
Суммарную функциональную погрешность за период времени
или более точно по формуле
где: n1 - число деталей, обработанных за время от K = 1,73; Постоянная погрешность определяется соответственно для наружной и внутренней обработки по формулам:
Суммарная погрешность обработки за период времени от 
При вычислении постоянных погрешностей используются формулы (25), в которой a1 надо заменить на a2. По величине для процессов I типа
для процессов II и III типов
где mk - номер последней группы; m1 - номер группы, соответствующей моменту времени τ1.
Пример. С токарного полуавтомата, настроенного на обработку валиков диаметром D = 55-0,2 взята большая текущая выборка объемом N = 50 шт. В таблице 6 приведены результаты измерения диаметра валиков в виде отклонений в мкм их размера от номинального значения D = 55 мм. Результаты измерения указаны в порядке изготовления деталей. Требуется установить, по данным выборки, является ли процесс устойчивым и какова его точность.
Таблица 6. Результаты измерения деталей выборки в мкм
Прежде всего, следует выяснить, к какому типу точности относится исследуемый процесс. Для этой цели, не прибегая к трудоемкой процедуре проверки гипотезы случайности выборки по методу последовательных разностей, можно воспользоваться графическим способом. Этот способ заключается в следующем. Выборка делится на группы по n шт. в порядке их изготовления. Для каждой группы вычисляются средние арифметические В данном примере выборка разбита на 10 групп по 5 шт. деталей в группе. Исходные данные, необходимые для дальнейших расчетов, приведены в таблице 7.
Таблица 7. Исходные данные для статистического анализа
В таблице 7 значения групповых средних Для устойчивости процесса I типа точности необходимо выполнение двух условий: 1) групповые дисперсии 2) связь
Выполнение первого условия устанавливается путем проверки гипотезы равенства дисперсий при помощи критерия G:
Критическое значение Gт при доверительной вероятности q = 0,05 равно Gт = 0,33 (таблица П10 приложения). Так как G < Gт то наша гипотеза подтверждается и, следовательно, первое условие устойчивости процесса соблюдается. Для проверки выполнения второго условия необходимо вначале вычислить параметры a и b уравнения Используя данные таблицы 7 для
Подставляя данные таблицы 7 для
Вычислив теоретические значения
Для расчета суммы случайных погрешностей вычислим σ по формуле
где
Для проверки гипотезы линейности связи вычислим критерий T:
По таблице П9 приложения для k1 = 10 - 2 = 8 и k2 = m(n - 1) = 10·4 = 40 и найдем Т0,05 = 2,18. Так как Т < T0,05, то гипотеза линейности связи Таким образом, в результате анализа установлено, что процесс является устойчивым во времени и относится к I типу точности. Теперь можно вычислить постоянные погрешности, случайные погрешности, резерв точности и время работы станка без подналадки
По формуле (20):
или
где t - штучное время обработки в мин.
Контрольные вопросы и задачи для приобретения знаний по теме 7
1. Перечислите процедуры, которые включает в себя статистический анализ точности методом больших выборок? 2. При принятии каких гипотез исследуемый процесс может быть отнесен к IV типу точности? 3. В краткой форме перечислите операции проверки о случайности и нормальном распределении выборки? 4. При достоверности каких гипотез исследуемый процесс обработки считается технологически устойчивым? 5. Возможен ли брак при достаточной точности процесса обработки? Если да, то в каких случаях?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 380. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 от τ будет установлено, что изучаемый процесс относится ко II или III типу точности, то проверку гипотезы линейности связи
от τ будет установлено, что изучаемый процесс относится ко II или III типу точности, то проверку гипотезы линейности связи  в диаграммах точности типа II и III рис. 5 темы 6).
в диаграммах точности типа II и III рис. 5 темы 6).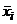 на участке от τ0 до τ1 диаграммы точности типа II (рисунок 5) и определяются для нее параметры a1 и b1 уравнения
на участке от τ0 до τ1 диаграммы точности типа II (рисунок 5) и определяются для нее параметры a1 и b1 уравнения  по способу наименьших квадратов. Вторая часть этой кривой на участке от τ1 до τk после выпрямления будет определяться уравнением
по способу наименьших квадратов. Вторая часть этой кривой на участке от τ1 до τk после выпрямления будет определяться уравнением  . Функциональные погрешности в данном случае для момента времени
. Функциональные погрешности в данном случае для момента времени  будут равны
будут равны  , а для момента
, а для момента 
 равны
равны  , где
, где (21)
(21) . (22)
. (22) приближенно можно определять по формуле
приближенно можно определять по формуле (23)
(23) , (24)
, (24) до
до 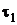 ; n2 — число деталей, обработанных за время от
; n2 — число деталей, обработанных за время от  ; n1 + n2 = mn - объем выборки;
; n1 + n2 = mn - объем выборки;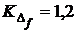 .
.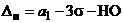 ;
;  . (25)
. (25) определяется по формулам (17) и (18).
определяется по формулам (17) и (18).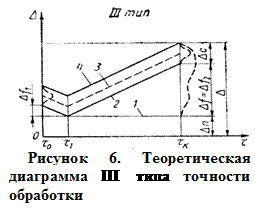 Определение погрешности обработки для процесса, относящегося к III типу точности. Если процесс относится к III типу точности, то при определении функциональной погрешности за время от
Определение погрешности обработки для процесса, относящегося к III типу точности. Если процесс относится к III типу точности, то при определении функциональной погрешности за время от  (рисунок 6).
(рисунок 6). для процессов I типа и по величине
для процессов I типа и по величине  ; (26)
; (26) , (27)
, (27)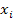
 , и строится график зависимости
, и строится график зависимости 

 На рисунке 7 приведена эмпирическая кривая изменений групповых средних
На рисунке 7 приведена эмпирическая кривая изменений групповых средних  , групповые дисперсии
, групповые дисперсии  - по формуле
- по формуле  .
.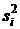 отличаются друг от друга случайно;
отличаются друг от друга случайно; .
.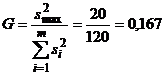 .
. и затем определить значения дисперсий
и затем определить значения дисперсий  и
и  для проверки гипотезы линейности регрессии
для проверки гипотезы линейности регрессии  (номера групп) и
(номера групп) и  . (28)
. (28) мкм.
мкм. по уравнению (28) и подставив их в формулу (16), найдем
по уравнению (28) и подставив их в формулу (16), найдем мкм.
мкм. ,
, по таблице П5 приложения для n = 50 равно 1,246. Следовательно,
по таблице П5 приложения для n = 50 равно 1,246. Следовательно, мкм
мкм .
.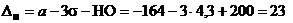 мкм;
мкм;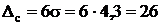 мкм;
мкм;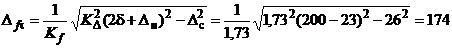 мкм;
мкм;
 ,
,