
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Логико-дидактический анализ темы «Применение производной к исследованию функций».Стр 1 из 3Следующая ⇒ Логико-дидактический анализ темы «Применение производной к исследованию функций» По учебнику «Алгебра и начала анализа 10-11 класс. Авторы: Ш.А.Алимов, Ю.М. Колягин, Ю.В.Сидоров и др.»
Выполнили: студентки группы М-5-В Соколова Ольга Сергеевна Место прохождения практики: МОУ СОШ №3 Руководитель: Шехмаметьева Галина Евгеньевна Дата прохождения практики:22.10.12 – 06.01.13
Самара 2012. Логико-дидактический анализ темы «Применение производной к исследованию функций». I. Цель изучения темы: дать систематические знания о применении производной к исследованию функции. Цель реализуется в следующих учебных задачах: Ø демонстрация возможностей производной в исследовании свойств функций и построении их графиков и применение производной к решению прикладных задач на оптимизацию; Ø отработка определения понятия производной; Ø раскрытие методики решения задач основных типов; Ø отработка умений применять теорию при решении задач; Ø определять значение функции по значению аргумента при различных способах задания функции; Ø строить графики изученных функций, выполнять преобразования графиков; Ø описывать по графику и по формуле поведение и свойства функций; Ø исследовать функции и строить их графики с помощью производной; Ø решать задачи с применением уравнения касательной к графику функции; Ø решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке; Новыми математическими фактами в этой теме будут: 1. Понятие возрастания и убывания функции (без доказательства). 2. Теорема Лагранжа (теорема 1).  3. Теорема о достаточном условии возрастания функции (теорема 2). 4. Понятие окрестности точки. 5. Понятие минимума/максимума функции. 6. Теорема Ферма (теорема 3). 7. Понятие стационарной точки. 8. Понятие критической точки. 9. Теорема о перемене знака производной, при переходе через стационарную точку (теорема 4). 10. Построение графика функции. 11. Нахождение наибольшего и наименьшего значения. 12. Понятие производной второго порядка. 13. Выпуклость функции. 14. Точки перегиба. 1. Понятие возрастания и убывания функции.
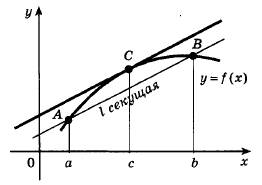
Объемом понятия являются все функции. Структура определенияконъюнктивная. Способ определениячерез ближайший род и видовые отличия. 2. Теорема 1 (Теорема Лагранжа). Если функция f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то существует такая точка с Î (a, b), что выполняется равенство f(b) − f(a) = f '(c)·(b − a). Условие теоремы: функция непрерывна и дифференцируема. Заключение теоремы: существует такая точка с Î (a, b), что выполняется равенство f(b) − f(a) = f '(c)·(b − a). Теорема сформулирована в условной форме. Структура теоремы сложная, т.к. в условии две посылки: 1) функция непрерывна на отрезке; 2) функция дифференцируема внутри него. Логическая связь между посылками конъюнктивная. 3. Теорема 2 (Теорема о достаточном условии возрастания функции). Если функция y = f(x) непрерывна на [a,b], дифференцируема на (a,b) и ее производная положительна на этом отрезке, f ' (x) ≥ 0 для a<x<b, то f(x) возрастает на [a,b]. Условие теоремы: функция непрерывна на отрезке, дифференцируема внутри него и производная положительна. Заключение теоремы: функция возрастает на отрезке. Теорема сформулирована в условной форме. Структура теоремы сложная, т.к. в условии три посылки: 1) функция непрерывна на отрезке; 2) функция дифференцируема внутри него; 3) производная положительна. Логическая связь между посылками конъюнктивная. 4. Понятие окрестности точки. Множество, содержащее данную точку, и близкие к ней. Объемом понятия являются все окрестности. Структура определенияконъюнктивная. Способ определениячерез ближайший род и видовые отличия. 5. Понятие минимума/максимума функции.
Объемом понятия являются все точки. Структура определенияконъюнктивная. Способ определениячерез ближайший род и видовые отличия. 6. Теорема 3 (Теорема Ферма). Пусть функцияf(x) определена и дифференцируема на интервале (a,b) и в некоторой точкеx0 этого интервала имеет наибольшее или наименьшее значение. Тогдаf'(x0) = 0. Условие теоремы: функция определена и дифференцируема на интервале и в некоторой точке имеет наибольшее или наименьшее значение Заключение теоремы: производная в этой точке равна нулю. Теорема сформулирована в условной форме. Структура теоремы сложная, т.к. в условии три посылки: 1) функция определена в интервале; 2) функция дифференцируема в интервале; 3) имеет наибольшее/наименьшее значение в точке. Логическая связь между посылками конъюнктивная. 7. Понятие стационарной точки. Точки, в которых производная функции равна нулю. Объемом понятия являются все точки. Структура определениядизъюнктивная. Способ определениячерез ближайший род и видовые отличия. 8. Понятие критической точки. Точки, в которых функция имеет производную, равную нулю, или недифференцируема. Объемом понятия являются все точки. Структура определениядизъюнктивная. Способ определениячерез ближайший род и видовые отличия. 9. Теорема 4 (Теорема о перемене знака производной, при переходе через стационарную точку). Пусть функция f(x) дифференцируема на интервале (a, b), x0 Î (a, b), и f’(x) = 0. Тогда:
Условие теоремы: функция дифференцируема на интервале, некоторая точка принадлежит этому интервалу, и производная в этой точке равна нулю и при переходе через стационарную точку меняет знак. Заключение теоремы: стационарная точка – точка максимума/минимума функции. Теорема сформулирована в условной форме. Структура теоремы сложная, т.к. в условии три посылки: 1) функция дифференцируема на интервале; 2) некоторая точка принадлежит этому интервалу; 3) производная в этой точке равна нулю и, при переходе через стационарную, меняет знак. Логическая связь между посылками конъюнктивная. 10. Построение графика функции. Задача. Построить график функции f(x) = x3 – 2x2 + x. Условие задачи: дана функция. Заключение: построить график этой функции с помощью производной. Задача на вычисление. Метод решения: алгоритмизация. Решение этой задачи показывает нам, как при помощи свойств производной функции построить график. Эта функция определена при всех x Î R. С помощью производной найдем промежутки монотонности этой функции и ее точки экстремума. Производная равна f ’(x) = 3x2 – 4x +1. Найдем стационарные точки: 3x2 – 4x +1= 0, откуда Для определения знака производной разложим квадратный трехчлен 3x2 – 4x +1 на множители: f '(x) = 3 (x - Производная положительна на промежутках x < При Точка Результаты исследования представим в следующей таблице:
Знак «↑» означает, что функция возрастает, а знак «↓» означает, что функция убывает. При построении графика обычно находят точки пересечения графика с осями координат. Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(x) = 0, находим точки пересечения графика с осью абсцисс:
Используя результаты исследования, строим график функции y = x3 – 2x2 + x.
11. Нахождение наибольшего и наименьшего значения. Задача. Найти наибольшее и наименьшее значения функции Условие задачи: дана функция. Заключение: найти наибольшее и наименьшее значения функции на отрезке [ Задача на вычисление. Метод решения: алгоритмизация. Решение этой задачи показывает нам алгоритм отыскания наибольшего и наименьшего значений функции. 12. Понятие производной второго порядка. Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом, f"(x) = (f'(x))'. Объемом понятия является функция. Структура определениядизъюнктивная. Способ определениячерез ближайший род и видовые отличия. 13. Понятие «выпуклость функции». Функция y = f(x), дифференцируемая на интервале (a, b), называется выпуклой вверх на этом интервале, если её производная f ' (x) убывает на (a, b). Аналогично функция f(x)называется выпуклой вниз на интервале (a, b), если f ' (x) возрастает на этом интервале, и поэтому f"(x) > 0. Объемом понятия является функция. Структура определенияконъюнктивная. Способ определениячерез ближайший род и видовые отличия. 14. Понятие «точки перегиба». Точка x0 дифференцируемой функции f(x) называется точкой перегиба этой функции, если x0 является одновременно концом интервала выпуклости вверх и концом интервала выпуклости вниз для f(x). Объемом понятия является точка. Структура определенияконъюнктивная. Способ определениячерез ближайший род и видовые отличия. |
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 458. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 x0 = 0 - max
x0 = 0 - max
 x0 = 2 - min
x0 = 2 - min



 ) (x – 1 ).
) (x – 1 ). является точкой максимума, так как слева от этой точки функция возрастает, а справа убывает. Значение функции в этой точке равно
является точкой максимума, так как слева от этой точки функция возрастает, а справа убывает. Значение функции в этой точке равно 
 является точкой минимума, так как слева от этой точки функция убывает, а справа возрастает; её значение в точке минимума равняется
является точкой минимума, так как слева от этой точки функция убывает, а справа возрастает; её значение в точке минимума равняется 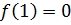 .
.


 x3 – 2x2 + x = 0, x(x2 – 2x + 1) = 0, x(x - 1)2 = 0,откуда x = 0, x = 1. Для более точного построения графика найдем значения функции еще в двух точках:
x3 – 2x2 + x = 0, x(x2 – 2x + 1) = 0, x(x - 1)2 = 0,откуда x = 0, x = 1. Для более точного построения графика найдем значения функции еще в двух точках: 
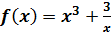 на отрезке [
на отрезке [  ].
]. ].
].