
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Примеры решения и оформления задачСтр 1 из 6Следующая ⇒ Варианты контрольных работ
Электромагнетизм. Колебания и волны.  Квантовая природа излучения. Элементы квантовой механики и ядерной физики Контрольная работа №3 Электромагнетизм. Колебания Законы и формулы
Магнитное поле Связь магнитной индукции B с напряженностью H магнитного поля:
где m — магнитная проницаемость изотропной среды; m 0 — магнитная постоянная (m 0 = 4p×10-7 Гн/м). В вакууме m = 1 и тогда магнитная индукция в вакууме
Закон Био-Савара-Лапласа:
или в скалярной форме
где dB — магнитная индукция поля, создаваемого элементом проводника длиной dl с током I; r — радиус-вектор, направленный от элемента проводника к точке, в которой вычисляется магнитная индукция; a — угол между радиусом-вектором и направлением тока в элементе проводника. Магнитная индукция в центре кругового тока:
где R — радиус кругового витка. Магнитная индукция на оси кругового тока:
где h — расстояние от центра витка до точки, в которой вычисляется магнитная индукция. Магнитная индукция поля прямого бесконечного тока:
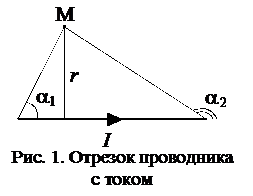
где r — расстояние от оси проводника до точки, в которой вычисляется магнитная индукция. Магнитная индукция поля, создаваемого отрезком провода с током:
где a1, a2 — углы, образованные проводником с током и радиусами-векторами, проведенными из концов проводника в точку M (рис. 1); r — расстояние от проводника до точки M, в которой вычисляется магнитная индукция. Магнитная индукция поля соленоида:
где n — число витков соленоида, приходящееся на единицу длины соленоида. Сила Ампера — сила взаимодействия проводника с током и магнитного поля:
где l — длина проводника, a — угол между проводником и вектором магнитной индукции. Направление силы Ампера можно определить по правилу левой руки. Магнитный момент контура с током:
где I — сила тока, протекающего по контуру; S — площадь контура; вектор S численно равен площади S контура и совпадает по направлению с вектором нормали к плоскости контура. Если магнитное поле создается рамкой, имеющей несколько витков, то необходимо просуммировать магнитные моменты, создаваемые отдельными витками. Если площади всех витков одинаковы, то
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
где a — угол между векторами pm и B. Сила Лоренца:
где v — скорость заряженной частицы; a — угол между векторами v и B. Магнитный поток:
где S — площадь контура; a — угол между нормалью к плоскости контура и вектором магнитной индукции. Для вычисления потока через поверхность сложной формы, такую, например, как поверхность, ограниченную витками катушки, следует найти потоки через отдельные участки поверхности (витки), а затем сложить эти потоки. Если катушка находится в однородном поле и все N витков имеют одинаковую площадь, то магнитный поток можно найти по формуле
Работа по перемещению замкнутого контура в магнитном поле:
Электромагнетизм ЭДС индукции (закон Фарадея):
Разность потенциалов на концах проводника, движущегося со скоростью v в магнитном поле:
где l — длина проводника; a — угол между векторами v и B. Заряд, протекающий по замкнутому контору при изменении магнитного потока, пронизывающего этот контур:
где R — сопротивление контура, N — число витков. ЭДС самоиндукции:
Индуктивность соленоида:
где n — число витков, приходящееся на единицу длины соленоида; V — объем соленоида. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L: а) при замыкании цепи:
где E — ЭДС источника тока; t — время, прошедшее после замыкания цепи; б) при размыкании цепи:
где I0 — значение силы тока в цепи при t = 0; t — время, прошедшее с момента размыкания цепи. Энергия магнитного поля:
Объемная плотность энергии магнитного поля (энергия, заключенная в единицу объема):
где B — магнитная индукция; H — напряженность магнитного поля.
Колебания
Уравнение гармонических колебаний:
где x — значение изменяющейся физической величины в момент времени t, А – амплитуда колебания, Скорость при гармонических колебаниях:
Ускорение при гармонических колебаниях:
Дифференциальное уравнение гармонических колебаний:
Период и частота колебаний математического маятника:
где l — длина нити, g — ускорение свободного падения. Период и частота колебаний физического маятника:
где J — момент инерции тела относительно оси вращения, m — масса тела, a — расстояние от центра инерции (центра масс) до оси вращения. Период и частота колебаний упругой системы:
где m — масса тела, k — жесткость пружины. Период электрических колебаний в идеальном электрическом контуре (формула Томсона):
где L — индуктивность, C — (электро)емкость контура. Полная энергия гармонических колебаний: а) для механических колебаний:
б) для электрических колебаний:
Уравнение затухающих механических колебаний:
где A0 — начальная амплитуда, Частота затухающих колебаний:
где w0 — частота свободных незатухающих колебаний. Логарифмический декремент затухания:
где An и An+1 — две соседние амплитуды колебаний одного знака. Связь логарифмического декремента с коэффициентом затухания:
где T — период затухающих колебаний, w — частота затухающих колебаний. Для затухающих электрических колебаний:
Примеры решения и оформления задач Пример 1. Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении токи силой I = 60 А расположены на расстоянии d = 10 см друг от друга. Определить индукцию магнитного поля в точке А, отстоящей от одного проводника на расстоянии r1 = 5 см и от другого на расстоянии r2 = 12 см.
Решение Для нахождения индукции магнитного поля B в указанной точке А (рис. 2) определим направление векторов индукции B1 и B2 полей, создаваемых каждым проводником в отдельности, и сложим их геометрически (по правилу параллелограмма), т.е. B = B1 + B2.
где a — угол между векторами B1 и B2. Значение индукций B1 и B2 выражаются соответственно через силу тока I и расстояния r1 и r2 от проводов до точки А, индукцию поля в которой мы вычисляем:
Подставляя B1 и B2 в формулу (1) и вынося Вычислим cos a. По теореме косинусов из треугольника ABC имеем:
где d — расстояние между проводниками. Отсюда
или
Подставляя в формулу (2) значения I, r1, r2 и значение cos a, определяем искомую индукцию:
Ответ: B = 3,08×10-4 Тл.
Пример 2. Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле напряженностью H = 103 А/м. Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.
Решение Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца FЛ (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение:
или Из формулы (1) найдем Входящий в равенство (2) импульс mv может быть выражен через кинетическую энергию T электрона: Но кинетическая энергия электрона, прошедшего ускоренную разность потенциалов U, определяется равенством
Подставив это выражение T в формулу (3), получим:
Магнитная индукция B может быть выражена через напряженность H магнитного поля в вакууме соотношением:
где m0 — магнитная постоянная. Подставляя найденные выражения B и mv в формулу (2), определим: Произведем вычисления:
Для определения частоты обращения n воспользуемся формулой, связывающей частоту со скоростью и радиусом: Подставив в формулу (5) выражение (2) для радиуса кривизны, получим:
или
Подставим их и произведем вычисления:
Ответ: n = 3,52×107 с-1.
Пример 3. Плоский квадратный контур со стороной a = 10 см, по которому течет ток I = 100 А, свободно установился в однородном магнитном поле B = 1 Тл. Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) j 1 = 90°; 2) j 2 = 3°. При повороте контура сила тока в нем поддерживается неизменной.
Решение Как известно, на контур с током в магнитном поле действует момент сил: По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (M = 0), а значит j = 0, т.е. векторы pm и B совпадают по направлению. Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j ), то для подсчета работы применим формулу работы в дифференциальной форме:
Подставив сюда выражение M по формуле (1) и учтя, что
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол: 1) Работа при повороте на угол j 1 = 90°:
Подставляя в полученную формулу числовые значения, получим: A1 = 100×1×(0,1)2 = 1 Дж. 2) Работа при повороте на угол j 2 = 3°. В этом случае, учитывая, что угол j2 мал, в выражении (2) значение синуса можно заменить значением угла, выраженным в радианах, то есть Переведем угол j 2 = 3° в радианы:
После подстановки числовых значений величин в (4) найдем:
Ответ: A1 = 1 Дж; A2 = 1,37 мДж.
Пример 4. В однородном магнитном поле B = 0,1 Тл равномерно с частотой n = 10об/с вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки S = 150 см2. Определить мгновенное значение ЭДС индукции, соответствующее углу поворота рамки в 30°.
Решение Мгновенное значение ЭДС индукции Ei определяется основным уравнением электромагнитной индукции Фарадея-Максвелла: где F — магнитный поток через рамку. В однородном поле поток через рамку, имеющую N витков, плотно прилегающих друг к другу, можно выразить соотношением: где B — магнитная индукция; S — площадь рамки. При вращении угол a можно выразить через частоту вращения по формуле
Подставим в формулу (2) выражение a, а получившуюся формулу для F подставим в (1):
Продифференцировав получившееся выражение по времени, найдем мгновенное значение ЭДС индукции: Выражение, стоящее под знаком синуса является фазой j , поэтому можно не определять момент времени, в который вычисляется ЭДС, а сразу подставить значение фазы из условия. Подставим в (3) числовые данные, получим:
Ответ: Ei = 47,1 В.
Пример 5. Определить период колебаний стержня длиной l = 30 см около оси, перпендикулярной стержню и проходящей через его конец.
Решение
Для физического маятника период колебаний около неподвижной оси: где J — момент инерции относительно этой оси, m — масса маятника, a — расстояние от оси колебаний до центра тяжести. Момент инерции относительно оси, проходящей через конец стержня можно определить по теореме Штейнера: где Jc — момент инерции относительно оси, параллельной данной и проходящей через центр тяжести. Но для стержня момент инерции: где l — длина стержня. Подставим (3) в (2), учитывая, что a = l/2 (рис. 7):
Подставим полученное выражение в (1):
Подставим значения величин, получим:
Ответ: T = 0,9 с.
Пример 6. Колебательный контур имеет емкость C = 1,1 нФ и индуктивность L = 5 мГн. Логарифмический декремент затухания равен 0,005. За какое время вследствие затухания потеряется 99 % энергии колебаний в контуре?
Решение Энергию колебаний в контуре можно записать по формуле
где I — максимальное (амплитудное) значение силы тока в контуре. Так как при затухании потерялось 99 % энергии, то оставшуюся в контуре энергию колебаний можно записать как
Сократив обе части выражения на L/2 и вычислив квадратный корень получим соотношение для сил токов
Амплитуда затухающих колебаний зависит от времени:
где A0 — начальная амплитуда, d — коэффициент затухания. В нашем случае I1 — начальная амплитуда, I2 — конечная амплитуда.
Прологарифмировав обе части уравнения, найдем время:
Коэффициент затухания связан с логарифмическим декрементом затухания по формуле
где T — период затухающих колебаний. По условию задачи логарифмический декремент мал, поэтому период затухающих колебаний приблизительно равен периоду собственных колебаний контура:
Найдем выражение для коэффициента затухания:
Подставим выражение для коэффициента затухания в формулу для времени:
Подставим в формулу числовые значения:
= 0,0068 с = 6,8 мс. Ответ: t = 6,8 мс.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 342. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
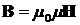 ,
,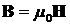 .
.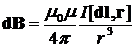
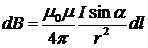 ,
,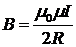 ,
,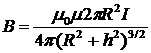 ,
,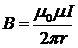 ,
,
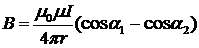 ,
,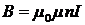 ,
,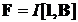 ,
, 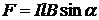 ,
,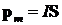 ,
,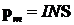 .
.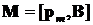 ,
, 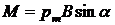 ,
,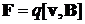 ,
, 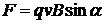 ,
,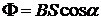 ,
, 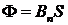 ,
,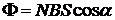 .
.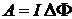 .
.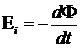 .
.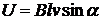 ,
,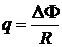 ,
, 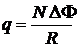 ,
,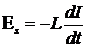 .
.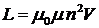 ,
,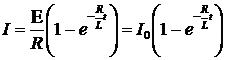 ,
,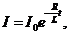
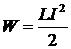 .
.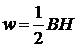 ,
, 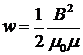 ,
, 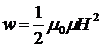 ,
,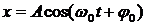 ,
,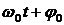 – полная фаза колебания, j 0 – начальная фаза, w0 – собственная круговая частота колебания.
– полная фаза колебания, j 0 – начальная фаза, w0 – собственная круговая частота колебания.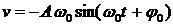 .
.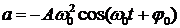 .
.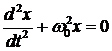 .
.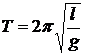 ,
, 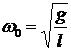 ,
,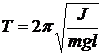 ,
, 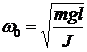 ,
,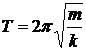 ,
, 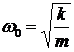 ,
,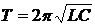 ,
,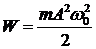 ;
;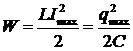 .
.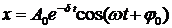 ,
,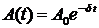 — амплитуда затухающих колебаний в момент времени t, w — частота затухающих колебаний, j 0 — начальная фаза, d — коэффициент затухания.
— амплитуда затухающих колебаний в момент времени t, w — частота затухающих колебаний, j 0 — начальная фаза, d — коэффициент затухания.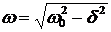 ,
,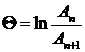 ,
,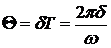 ,
,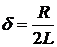 .
.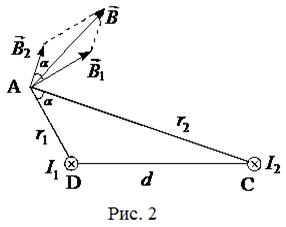 Абсолютное значение индукции B может быть найдено по теореме косинусов:
Абсолютное значение индукции B может быть найдено по теореме косинусов: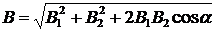 , (1)
, (1)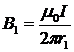 ,
, 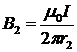 .
.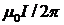 за знак корня, получим:
за знак корня, получим: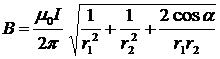 . (2)
. (2)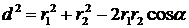 ,
,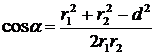 ,
,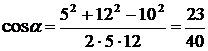 .
.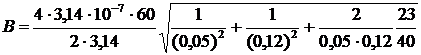 = 3,08×10-4 Тл.
= 3,08×10-4 Тл.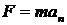 ,
,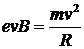 . (1)
. (1)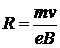 . (2)
. (2)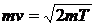 . (3)
. (3)
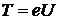 .
.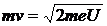 .
.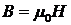 ,
,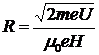 . (4)
. (4)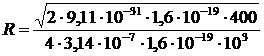 = 5,37×10-2 м = 5,37 см.
= 5,37×10-2 м = 5,37 см.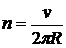 . (5)
. (5)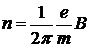 ,
,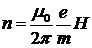 .
.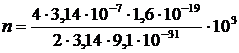 = 3,52×107 с-1.
= 3,52×107 с-1.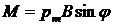 . (1)
. (1)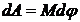 .
.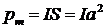 , где I — сила тока в контуре;
, где I — сила тока в контуре; 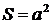 — площадь контура, получим:
— площадь контура, получим: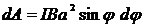 .
.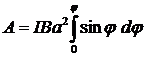 . (2)
. (2)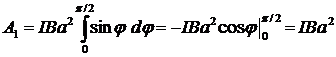 .
.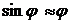 :
: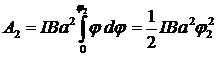 . (4)
. (4)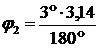 = 0,0524 рад.
= 0,0524 рад.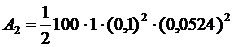 = 1,37×10-3 Дж = 1,37 мДж.
= 1,37×10-3 Дж = 1,37 мДж.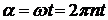 .
.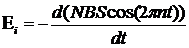 .
.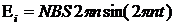 . (3)
. (3)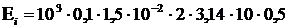 = 47,1 В.
= 47,1 В.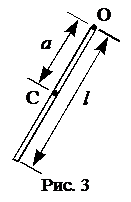 Стержень, имеющий возможность совершать вращение около горизонтальной оси O, не проходящей через центр масс (центр тяжести) C, есть физический маятник (рис. 3).
Стержень, имеющий возможность совершать вращение около горизонтальной оси O, не проходящей через центр масс (центр тяжести) C, есть физический маятник (рис. 3).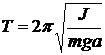 , (1)
, (1)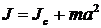 , (2)
, (2)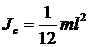 , (3)
, (3)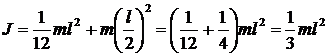 .
.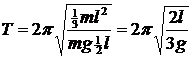 .
.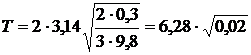 = 0,9 с.
= 0,9 с.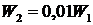 или
или 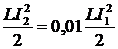 .
.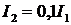 .
.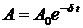 ,
,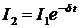 или
или 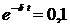 .
.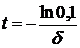 .
.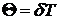 ,
,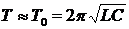 .
.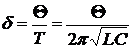 .
.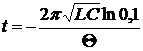 .
.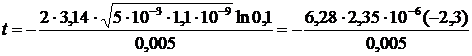 =
=