Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Для задачи (5.11), (5.12) функция Лагранжа будет иметь вид
Если функция имеет седловую точку (
5.3.2 Метод неопределенных множителей Лагранжа для решения задач квадратичного программирования
Рассмотрим задачу (5.11), (5.12) из пункта 5.3.1. Чтобы найти решение задачи квадратичного программирования (5.11), (5.12) нужно определить неотрицательное решение систем линейных уравнений (5.13). Это решение можно найти с помощью метода искусственного базиса. Процесс нахождения решения включает следующие этапы: 1) составляют функцию Лагранжа; 2) записывают в виде системы (5.13) необходимые и достаточные условия существования седловой точки для функции Лагранжа; 3) используя метод искусственного базиса, либо устанавливают отсутствие седловой точки для функции Лагранжа, либо находят ее координаты; 4) записывают оптимальное решение исходной задачи и находят значение целевой функции. Пример 5.3. Найти максимальное значение функции при условиях
Решение. Функция f является вогнутой, так как представляет собой сумму линейной функции
и запишем необходимые и достаточные условия существования седловой точки построенной функции: 
Систему линейных неравенств (5.17) перепишем в виде:
Вводя теперь дополнительные неотрицательные переменные v1,v2,w1 и w2, обращающие неравенства (5.17) в равенства, получим Учитывая равенства (5.20), можно записать: Если теперь найти базисное решение системы линейных уравнений (5.20) с учетом (5.21), то будет получена седловая точка функции Лагранжа для исходной задачи, то есть определено оптимальное решение. Для нахождения базисного решения системы линейных уравнений (5.20) воспользуемся методом искусственного базиса. В первое и второе уравнения (5.20) добавим неотрицательные переменные Z1 и Z2 и рассмотрим задачу линейного программирования, состоящую в определении максимального значения функции
при условиях
В результате решения задачи линейного программирования (5.22)−(5.24) находим допустимое базисное решение системы линейных уравнений (5.23) (таблица 5.1): Отсюда Так как
Таблица 5.1 – Результаты вычислений методом Лагранжа
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 274. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. ,
,  ), то в этой точке выполняются соотношения (5.9). Вводя дополнительные переменные
), то в этой точке выполняются соотношения (5.9). Вводя дополнительные переменные  и
и  , перепишем выражения (5.9) в виде
, перепишем выражения (5.9) в виде (5.13)
(5.13) (5.14)
(5.14)
 (5.15)
(5.15) (которую можно рассматривать как вогнутую) и квадратичной формы
(которую можно рассматривать как вогнутую) и квадратичной формы 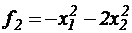 , которая является отрицательно определенной. Система ограничений включает только линейные неравенства. Следовательно, можно воспользоваться теоремой Куна-Таккера. Составим функцию Лагранжа:
, которая является отрицательно определенной. Система ограничений включает только линейные неравенства. Следовательно, можно воспользоваться теоремой Куна-Таккера. Составим функцию Лагранжа: (5.16)
(5.16) (5.17)
(5.17) (5.18)
(5.18) (5.19)
(5.19) (5.20)
(5.20) .
. . (5.21)
. (5.21)
 (5.22)
(5.22) (5.23)
(5.23) . (5.24)
. (5.24) .
. , то (
, то (  =(1,1) – оптимальный план исходной задачи и fmax=3.
=(1,1) – оптимальный план исходной задачи и fmax=3.