
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рассмотрим задачу нелинейного программирования.Минимизировать (максимизировать) при условиях Для решения этой задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых имеются дополнительные ограничения относительно свойств функций f и gi, разработаны эффективные методы их решения. В частности, ряд таких методов имеется для решения задач при условии, что f – выпуклая (вогнутая) функция и область допустимых решений, определяемая (5.6) и (5.7) – выпуклая. Дадим определения и понятия, необходимые нам в дальнейшем.
5.3.1 Основные определения и теоремы
ОПРЕДЕЛЕНИЕ 5.1. Непустое множество S из Еn называется выпуклым, если отрезок прямой, соединяющий две любые точки множества S также принадлежит этому множеству. Иными словами, если точки На рисунке 5.3 приведены примеры множеств.
Рисунок 5.3 – Примеры множеств: а) – выпуклое; б) – невыпуклое
ОПРЕДЕЛЕНИЕ 5.2. Пусть для любых При этом, если имеет место строгое неравенство, то говорят о строгой выпуклости. Функция f называется вогнутой, если −f выпукла на S. На рисунке 5.4 приведены примеры выпуклых и вогнутых функций.
Рисунок 5.4 – Функции : а) – выпуклая функция; б) – вогнутая функция; в) – функция, не являющаяся ни вогнутой, ни выпуклой.  Замечания.1.Из определения квазивыпуклой функции в п.4.1 очевидно следует, что выпуклая функция является также и квазивыпуклой, причем строго квазивыпуклой. Таким образом,предположение о квазивыпуклости исследуемой функции является существенно более слабым, чем выпуклость этой функции. 2. Строго квазивыпуклые (квазивогнутые) функции особенно важны в нелинейном программировании,т.к. для этих функций локальный минимум (максимум) на выпуклом множестве соответственно являются глобальными минимумом и максимумом. ОПРЕДЕЛЕНИЕ 5.3. Говорят, что множество допустимых решений задачи (5)−(6) удовлетворяет условию регулярности, если существует по крайней мере одна точка
ОПРЕДЕЛЕНИЕ 5.4.Задача (5)−(6) называется задачей выпуклого программирования, если функция f является вогнутой (выпуклой), а функции gi – выпуклыми. ОПРЕДЕЛЕНИЕ 5.5. Пусть ОПРЕДЕЛЕНИЕ 5.6. Функцией Лагранжа задачи выпуклого программирования называется функция
где ОПРЕДЕЛЕНИЕ 5.7. Точка
для всех ТЕОРЕМА 5.1. Любой локальный минимум (максимум) задачи выпуклого программирования является глобальным минимумом (максимумом). ТЕОРЕМА 5.2. (Теорема Куна-Таккера). Для задачи выпуклого программирования (5.5)−(5.6), множество допустимых решений которой обладает свойством регулярности, точка Если предположить, что целевая функция f и функции gi в (5.5)−(5.6) непрерывно дифференцируемы, то теорема Куна-Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка (
где ОПРЕДЕЛЕНИЕ 5.8. Квадратичной формой относительно переменных
ОПРЕДЕЛЕНИЕ 5.9. Квадратичная форма f называется положительно (отрицательно)−определенной, если ТЕОРЕМА 5.3. Квадратичная форма является выпуклой функцией, если она положительно−полуопределенная, и вогнутой функцией, если она отрицательно − полуопределенная. ОПРЕДЕЛЕНИЕ 5.10. Задача, состоящая в определении минимального (максимального) значения функции при условиях
где |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 241. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (5.5)
(5.5)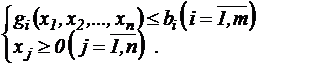 (5.6)
(5.6)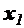 и
и  лежат в S, то точка
лежат в S, то точка  также должна принадлежать S для всех
также должна принадлежать S для всех  .
.

 , где S – непустое выпуклое множество в En Говорят, что функция f выпукла на S, если
, где S – непустое выпуклое множество в En Говорят, что функция f выпукла на S, если (5.7)
(5.7)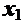 ,
, 
 S и
S и  .
.

 а) б) в)
а) б) в) , принадлежащая области допустимых решений такая, что
, принадлежащая области допустимых решений такая, что .
.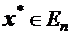 . Если
. Если 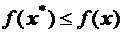 для всех
для всех  называется точкой глобального минимума функции f. Если существует ε − окрестность
называется точкой глобального минимума функции f. Если существует ε − окрестность  точки
точки  такая, что
такая, что  , то
, то 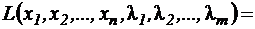
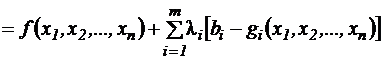 , (5.8)
, (5.8)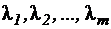 - неопределенные множители Лагранжа.
- неопределенные множители Лагранжа. называется седловой точкой функции Лагранжа, если
называется седловой точкой функции Лагранжа, если


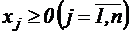 и
и  .
. является оптимальным решением тогда и только тогда, когда существует такой вектор
является оптимальным решением тогда и только тогда, когда существует такой вектор 
 , что (
, что (  ,
,  ) – седловая точка функции Лагранжа.
) – седловая точка функции Лагранжа.


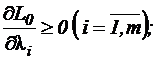 (5.9)
(5.9) 
 и
и  − значения соответствующих частных производных функций Лагранжа, вычисленных в седловой точке. Всем отмеченным выше требованиям, позволяющим записать необходимые и достаточные условия для седловой точки (
− значения соответствующих частных производных функций Лагранжа, вычисленных в седловой точке. Всем отмеченным выше требованиям, позволяющим записать необходимые и достаточные условия для седловой точки (  называется скалярная функция от этих переменных, имеющая вид:
называется скалярная функция от этих переменных, имеющая вид:
 . (5.10)
. (5.10)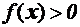
 для всех значений переменных
для всех значений переменных  кроме
кроме 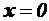 . Если же имеют место нестрогие равенства, то квадратичная форма f называется положительно (отрицательно)-полуопределенной.
. Если же имеют место нестрогие равенства, то квадратичная форма f называется положительно (отрицательно)-полуопределенной.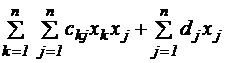 (5.11)
(5.11)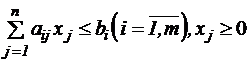 , (5.12)
, (5.12)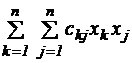 - положительно (отрицательно) - полуопределенная квадратичная форма, называется задачей квадратичного программирования.
- положительно (отрицательно) - полуопределенная квадратичная форма, называется задачей квадратичного программирования.