
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрическая интерпретация решения задач нелинейного программированияСтр 1 из 4Следующая ⇒ Задачи нелинейного программирования Постановка задачи и основные определения Выше рассматривались задачи линейного программирования. Это задачи, в которых все фигурирующие функции линейные. Однако большинство реальных задач не может быть адекватно описано с помощью моделей линейного программирования из-за нелинейности целевой функции или некоторых ограничений. В частности, в виде моделей нелинейного программирования можно представить задачи оптимизации, возникающие в следующих областях: 1) оптимальное управление; 2) проектирование строительных конструкций; 3) проектирование механических конструкций; 4) электрические цепи; 5) управление водными ресурсами; 6) распределение ресурсов в условиях неполной информации; 7) размещение оборудования. Общая задача нелинейного программирования имеет вид: минимизировать (максимизировать) целевую функцию
f(x1, x2, …, xn) (5.1)
при условиях
где f и gi – некоторые известные функции n переменных, а bi – заданные числа. В результате решения задачи (1), (2) должна быть определена точка
координаты которой удовлетворяют соотношениям (2) и такая, что для всякой другой точки
[
Соотношения (2) могут включать и условия неотрицательности переменных. Если все функции f и gi – линейные, то задача (1), (2) называется задачей линейного программирования. В противном случае имеем задачу нелинейного программирования.  Задачу (1), (2) можно записать сокращенно в векторной форме: минимизировать (максимизировать) целевую функцию
при условиях
Здесь f и gi – определенные в евклидовом пространстве Еn функции. Совокупность всех векторов размерности n образует n-мерное евклидово пространство Еn. В пространстве Еn система ограничений (2) определяет область допустимых решений задачи. В отличие от задачи линейного программирования она всегда является выпуклой. Если определена область допустимых решений, то нахождение решения задачи (1), (2) сводится к определению такой точки этой области, через которую проходит гиперповерхность наинизшего (наивысшего) уровня:
Геометрическая интерпретация решения задач нелинейного программирования
Процесс нахождения решения задачи нелинейного программирования (1), (2) геометрическим способом состоит из следующих этапов: 1) нахождение области допустимых решений задачи, определяемой соотношениями (2) (если она пуста, то задача не имеет решения); 2) построение гиперповерхности 3) определение гиперповерхности наинизшего (наивысшего) уровня или установление неразрешимости задачи из-за неограниченности функции (1) снизу (сверху) на множестве допустимых решений; 4) нахождение точки области допустимых решений, через которую проходит гиперповерхность наинизшего (наивысшего) уровня и нахождение значения функции (1) в этой точке. Пример 5.1. Минимизировать функцию при условиях
Целевая функция и три ограничения имеют вид
Здесь функции f(x) и g1(x) нелинейные, поэтому имеем задачу нелинейного программирования. На рисунке 5.1 изображена допустимая область.
Рисунок 5.1 – Допустимая область для примера 5.1
Задача заключается в нахождении такой точки из допустимой области, для которой Пример 5.2. Максимизировать при условиях На рисунке 5.2 изображена допустимая область задачи в виде многоугольника ОАВС. Следовательно, для нахождения ее решения нужно определить такую точку многоугольника ОАВС, в которой целевая функция
Рисунок 5.2 – Допустимая область для примера 5.2
Построим линию уровня Точка D (3,4) – оптимальное решение и значение целевой функции в этой точке равно 13. Как видно из примера 5.2, точка максимального значения целевой функции не является вершиной допустимой области. Поэтому процедура перебора вершин, используемая при решении задачи линейного программирования, не применима для решения данной задачи. |
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 307. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
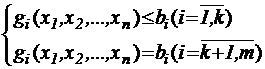 , (5.2)
, (5.2) ,
, , удовлетворяющей условиям (2), выполняется неравенство
, удовлетворяющей условиям (2), выполняется неравенство
 или
или 
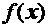 (5.3)
(5.3) . (5.4)
. (5.4)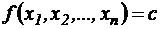 . Указанная точка может находиться как на границе области допустимых решений, так и внутри нее.
. Указанная точка может находиться как на границе области допустимых решений, так и внутри нее.




 .
.


 , лежат на окружности радиуса
, лежат на окружности радиуса 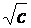 с центром в точке (3,2). Для каждого неотрицательного c такая окружность называется линией уровня целевой функции, отвечающей заданному значению c. Таким образом, задача заключается в нахождении минимального c, при котором хотя бы одна точка окружности принадлежит допустимой области. Как видно на рисунке 5.1, такая окружность наименьшего радиуса соответствует c=2 и пересекает допустимую область в единственной точке А(2,1). Поэтому точка А(2,1) - оптимальное решение, и значение целевой функции в этой точке равно 2.
с центром в точке (3,2). Для каждого неотрицательного c такая окружность называется линией уровня целевой функции, отвечающей заданному значению c. Таким образом, задача заключается в нахождении минимального c, при котором хотя бы одна точка окружности принадлежит допустимой области. Как видно на рисунке 5.1, такая окружность наименьшего радиуса соответствует c=2 и пересекает допустимую область в единственной точке А(2,1). Поэтому точка А(2,1) - оптимальное решение, и значение целевой функции в этой точке равно 2.

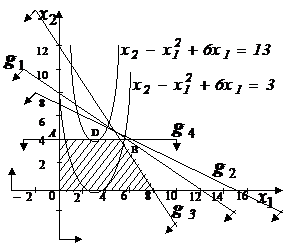
 и исследуем ее поведение при различных значениях с. При каждом значении с получаем параболу, которая тем выше отдалена от оси Ох1, чем больше значение с. Целевая функция принимает максимальное значение в точке касания одной из парабол с границей многоугольника ОАВС. В данном случае это точка D, в которой линия уровня
и исследуем ее поведение при различных значениях с. При каждом значении с получаем параболу, которая тем выше отдалена от оси Ох1, чем больше значение с. Целевая функция принимает максимальное значение в точке касания одной из парабол с границей многоугольника ОАВС. В данном случае это точка D, в которой линия уровня  касается допустимой области. Координаты точки D найдем из системы уравнений:
касается допустимой области. Координаты точки D найдем из системы уравнений: