
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методические указания к лабораторной работе № 2Исследуемая система (рис. 5) состоит из трёх апериодических звеньев, входящих в прямой канал (звенья 1 и 2) и в обратную связь (звено 3). Характерной особенностью таких систем является склонность их к перерегулированию и колебаниям. При определённом сочетании параметров в подобных системах могут возникнуть незатухающие или расходящиеся колебания, т. е. система может стать неустойчивой. Для построения результирующей ЛЧХ встречно-параллельно соединённых звеньев можно воспользоваться следующей методикой. Пусть имеются встречно-параллельно соединённые звенья с передаточной функцией прямого канала W1(p) и передаточной функцией W2(p) канала ОС (рис. 6 а). Таким образом, известны АФЧХ прямого канала Понятие обратных частотных характеристик звена обратной связи следующее: – обратная АЧХ – обратная ФЧХ – обратная ЛАЧХ Таким образом, обратные ЛЧХ являются зеркальным отображением прямых ЛЧХ относительно оси абсцисс (оси lgw). Известно, что передаточная функция встречно-параллельного соединения звеньев с ООС определяется соотношением
для частотных характеристик
В общем случае в некоторой области частот может соблюдаться соотношение Тогда уравнение (2.2) можно представить в виде
Очевидно, что в знаменателе дроби стоит выражение, мало отличающееся от единицы. В оставшейся области частот Тогда, представив уравнение (2.2) в виде

можно снова отметить, что в знаменателе дроби стоит выражение, мало отличающееся от единицы. Таким образом, результирующая АФЧХ встречно-параллельно соединённых звеньев с ООС идёт по АФЧХ прямого канала в области частот, где
во втором. Переходя к ЛЧХ, последнее можно сформулировать следующим образом. Результирующая ЛЧХ встречно-параллельного соединенных звеньев с ООС идёт по ЛЧХ прямого канала в области частот, где
Нахождение поправочного вектора
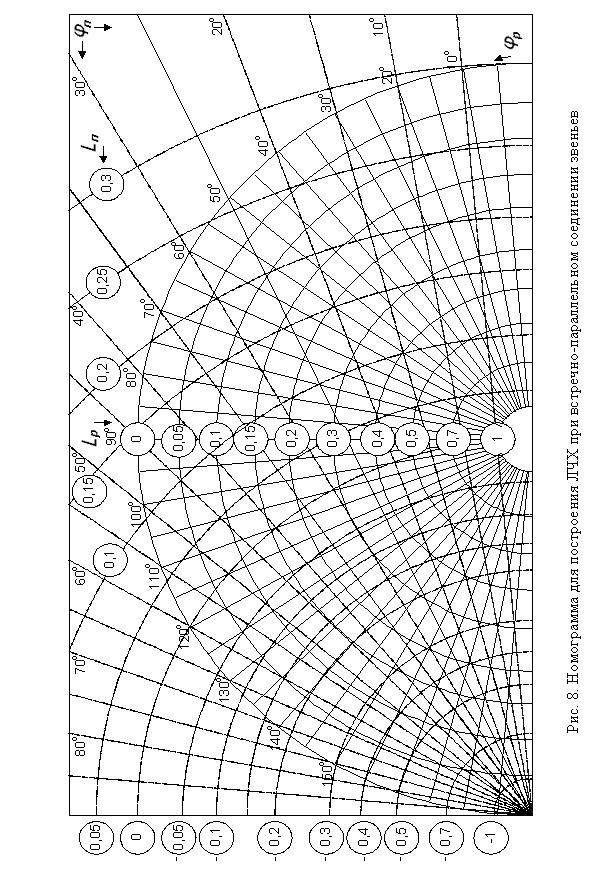
иллюстрируется векторной диаграммой (рис. 6 в). Для удобства нахождения поправочных координат на рис. 7 приведена номограмма, в которой вместо абсолютных значений амплитуд Таким образом, для построения результирующей ЛЧХ встречно-параллельно соединённых звеньев (рис. 6 б) необходимо: – построить – задавшись частотой wi , определить – по – значение LП(wi) отнимается от значения L12(wi) или L3(wi), лежащих ниже относительно друг друга, с учётом знака поправки, полученной по номограмме; – значение jП(wi) откладывается от фазы звена, ЛАЧХ (или обратная ЛАЧХ) которого лежит ниже. jП(wi) откладывается всегда вовнутрь пространства, лежащего между j12(w) и j3-1(w);
– повторяя построение для других частот аналогично изложенному, находят координаты L(w) и j(w) результирующей ЛЧХ. Наибольшие поправки будут в частоте пересечения В пределе при Установившееся значение регулируемой величены определяется значением результирующей ЛАЧХ в области малых частот (при w = 0 в пределе), поэтому следует обратить внимание на определение поправок в области низких частот. Если учесть, что В данной работе исследуется устойчивая система. При этом варианты для членов бригады подобраны так, что подъём результирующей ЛАХ в одном случае почти отсутствует, в другом варианте он в основном определяется инерционностью ОС, в третьем варианте он появляется в основном за счёт поправок. Первому случаю соответствует монотонный переходный процесс, второму – переходный процесс с большим перерегулированием, третьему – колебательный переходный процесс. Переходный процесс в первых двух случаях может быть построен по методике, описанной в п. 2.1.3 (рис. 4). В третьем случае переходный процесс может быть построен, если САУ представить эквивалентным колебательным звеном второго порядка. При этом частота Вопросы для самопроверки 1. Как построить результирующие ЛЧХ при встречно-параллельном соединении звеньев? 2. При каких условиях в замкнутой САУ возникают колебания выходной величины? 3. С помощью ЛЧХ пояснить влияние значения ТОС на качество переходного процесса. Литература [1, c. 110–123, 225–228]; [3, с. 82–88, 207–210, 255–259].
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 507. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
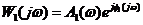 и соответственно ЛЧХ –
и соответственно ЛЧХ – 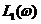 и
и 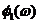 . АФЧХ канала обратной связи
. АФЧХ канала обратной связи 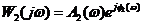 и соответственно ЛЧХ –
и соответственно ЛЧХ – 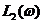 и
и 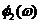 .
.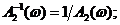
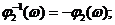
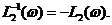
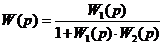 , (2.1)
, (2.1)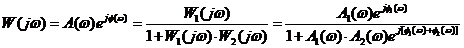 . (2.2)
. (2.2)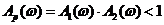 , или
, или 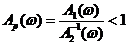 , т. е.
, т. е. 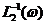 .
.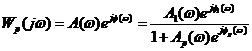 . (2.3)
. (2.3)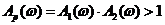 , или
, или 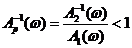 , т. е.
, т. е. 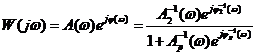 , (2.4)
, (2.4)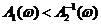 и по обратной АФЧХ канала ОС в области частот, где
и по обратной АФЧХ канала ОС в области частот, где 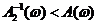 с учётом поправочного коэффициента, равного в первом случае
с учётом поправочного коэффициента, равного в первом случае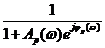 и
и 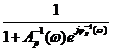 (2.5)
(2.5)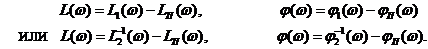
 Рис. 6. Структурная схема (а), ЛЧХ (б), поправочный вектор (в)
Рис. 6. Структурная схема (а), ЛЧХ (б), поправочный вектор (в)  , (2.6)
, (2.6)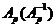 и
и 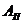 , даны их логарифмы, т. е.
, даны их логарифмы, т. е. 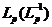 и
и 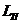 .
.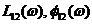 прямого канала и
прямого канала и 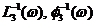 канала ОС;
канала ОС;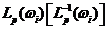 как расстояния между
как расстояния между 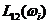 и
и 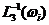 , а
, а 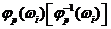 как расстояние между
как расстояние между 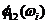 и
и 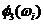 (рис. 6 б);
(рис. 6 б);
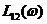 и
и 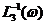 – частоте среза wС замкнутого контура. Действительно, при этой частоте
– частоте среза wС замкнутого контура. Действительно, при этой частоте 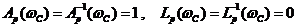 и величина поправки будет полностью определяться фазой
и величина поправки будет полностью определяться фазой 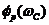 . При
. При 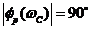 поправка будет 0,15 лог, что соответствует поправке аппроксимированного апериодического звена, т. е. в этом случае переходный процесс будет иметь апериодический характер, время регулирования составит примерно (3 – 4)/wC. При
поправка будет 0,15 лог, что соответствует поправке аппроксимированного апериодического звена, т. е. в этом случае переходный процесс будет иметь апериодический характер, время регулирования составит примерно (3 – 4)/wC. При 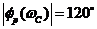 поправка в частоте wС равна нулю – процесс может иметь перерегулирование 18–25 % и колебательность
поправка в частоте wС равна нулю – процесс может иметь перерегулирование 18–25 % и колебательность 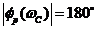 система находится на грани устойчивости, и в ней возникают незатухающие колебания с частотой wС. Амплитуда поправки при этом равна нулю, а
система находится на грани устойчивости, и в ней возникают незатухающие колебания с частотой wС. Амплитуда поправки при этом равна нулю, а 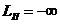 , т. е. результирующая ЛАЧХ имеет бесконечное возрастание (разрыв) в частоте среза.
, т. е. результирующая ЛАЧХ имеет бесконечное возрастание (разрыв) в частоте среза. 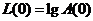 , то правильность нахождения поправок при w = 0 можно проверить определением А(0), придавая в формуле (2.2) w = 0 (или полагая в формуле (2.1) р= 0).
, то правильность нахождения поправок при w = 0 можно проверить определением А(0), придавая в формуле (2.2) w = 0 (или полагая в формуле (2.1) р= 0).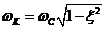 (период ТК = 2p/wK) и постоянная затухания
(период ТК = 2p/wK) и постоянная затухания 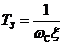 зависят от коэффициента демпфирования x. По аналогии с колебательным звеном x может быть определён высотой g всплеска ЛАЧХ типа L (рис. 7, б), т. е.
зависят от коэффициента демпфирования x. По аналогии с колебательным звеном x может быть определён высотой g всплеска ЛАЧХ типа L (рис. 7, б), т. е. 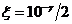 . Построение приближённой кривой переходного процесса
. Построение приближённой кривой переходного процесса