
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Этапы эконометрического моделирования
Выделим четыре основных этапа эконометрического моделирования. Первый этап: постановка задачи. Здесь формулируется цель исследования, определяются широта и глубина исследования, источники информации, формируется программа исследования, проводится сбор данных. Одна из проблем здесь - балансирование между научной корректностью исследования и его рентабельностью. Например, чем больше риск от планируемого мероприятия (а риск тем больше, чем больше вероятность неудачи и размер возможных потерь), тем больших затрат требует исследование. В рамках программы определяются все наблюдаемые зависимые и входные переменные. Из последних отбираются наиболее значимые - кандидаты в объясняющие переменные X1, X2, ... , Xp . Цель исследования обычно состоит в построении корректной эконометрической модели, с помощью которой можно анализировать поведение экономического объекта, включая прогнозирование, имитацию поведения, выработку управленческих решений. Объясняющих переменных не должно быть слишком много. Чрезвычайно желательно, чтобы они были практически взаимонезависимыми. В противном случае мы столкнемся с проблемой ультиколлинеарности (взаимозависимости) объясняющих переменных. Такие переменные неинформативны, без пользы усложняют модель и ее смысловую интерпретацию (теорию объекта), снижают корректность модели вплоть до невозможности ее построения. На практике при подозрении на наличие мультиколлинеарности применяют специальные процедуры отбора значащих малозависимых объясняющих переменных. Для оценки влияния качественных признаков (пол, образование, система налогообложения, отраслевая принадлежность и пр.) вводятся фиктивные объясняющие переменные. Например, пол можно выразить через булевскую переменную Х7 с двумя значениями: х7=0 – мужской, х7=1 – женский. Ясно, что эти значения условны – фиктивны.  Второй этап: построение (спецификация) эконометрической модели. На основе собранных данных и предварительных исследований проводится глубокий анализ моделируемого объекта, динамики его развития, его связей с внешней средой. Анализируется полнота, достоверность данных, формируются показатели. Проводится спецификация модели: выбирается тип функции f(X), состав объясняющих переменных, в том числе лаговых - при необходимости. Далее определяются все параметры модели. Как правило, на этом и последующих этапах используются специальные эконометрические пакеты программ, которые позволяют быстро проводить большой объем вычислений. Третий этап: верификация модели. Здесь проверяется адекватность модели, точность и надежность получаемых с ее помощью результатов. Для верификации могут использоваться модели-аналоги, привлекаться эксперты, выполняться прогнозно-аналитические расчеты на прошлых подобных ситуациях в данном регионе, в других регионах и странах. Четвертый этап: применение модели. На основе полных и достоверных исходных данных решается та задача, которая была сформулирована на 1-м этапе как цель исследования. Такая задача может быть одна или их может быть несколько. Наконец, эконометрическая модель может использоваться регулярно в рамках какой-нибудь информационной системы управления (мониторинг, прогнозирование, анализ, разработка управленческого решения и пр).
Вопросы для самоконтроля 1. Дайте определения модели, математической модели, моделирования, эконометрической модели. 2. Охарактеризуйте идею моделирования по принципу черного ящика, его связь с эконометрической моделью, типы переменных. 3. Раскройте содержание понятия: регрессионная модель. 4. Чем обусловлены проблемы получения больших однородных выборок? 5. Что такое пространственные и временные данные? 6. В чем суть гомоскедастичности дисперсии ошибок? 7. Каким четырем условиям удовлетворяют (или нет) ошибки регрессии? 8. Какие методы (приемы) сочетаются в процедуре спецификации функции, сколько их? 9. Назовите достоинства и недостатки линейных регрессионных моделей. 10. Какие линейные регрессионные модели называются классическими? 11. В чем отличие системы одновременных уравнений регрессии от простого набора регрессионных уравнений? 12. Что такое лаговая переменная, чем она отличается от обычной объясняющей переменной? 13. В чем суть процедуры спецификации модели? 14. В чем суть процедуры верификации модели, назовите несколько приемов верификации.
Линейная парная регрессия Методы и модели регрессионного анализа занимают центральное место в математическом инструментарии эконометрики. Наиболее часто используется парная регрессия, когда рассматривается пара переменных: одна объясняющая (синонимы - входная, экзогенная, регрессор) переменная Х и одна – объясняемая (синонимы - выходная, результирующая) переменная Y – обязательно случайная величина. Регрессией называют функцию, отражающую зависимость математического ожидания (МО) СВ Y от значений Х (такую зависимость называют также корреляционной). По определению регрессия есть условное МО СВ Y:
На практике точно не известно условное МО СВ Y, т.е. функция j(х). Поэтому можно говорить лишь о приближенном построении - оценке такой функции. Исходными данными для этого служат n пар значений Х и Y: xi и yi при i=1, 2, ... , n. В случае парной линейной регрессии в качестве оценки - выборочного уравнения регрессии - принимается прямая линия:
Неизвестные параметры bo и b1, как правило, определяются методом наименьших квадратов: значения параметров должны доставлять минимум сумме квадратов отклонений наблюденных значений yi от теоретических значений
Теоретически для оценки параметров bo и b1 можно использовать и метод наименьших модулей отклонений å ç Для отыскания значений параметров bo и b1 эконометрической модели (2.2) с помощью МНК приравниваем нулю частные производные S по bo и b1 и получаем систему двух уравнений:
Отсюда после преобразований получаем систему двух линейных уравнений с двумя неизвестными bo и b1:
Разделим 1-е уравнение на n и получим полезное соотношение: линия регрессии проходит через точку средних значений (
Разрешая (2.6) относительно bo , подставляя это значение во 2-е уравнение системы (2.5), получим искомые формулы для расчета значений параметров уравнения регрессии:
где sx2 - выборочная дисперсия переменной Х:
Параметр b1 называется коэффициентом регрессии (выборочным). Он показывает, на сколько единиц в среднем возрастет (уменьшится) Параметр b0 в зависимости от задачи может иметь смысл, а может и не иметь. Например, если Пример 2.1 [4, с.10]. Построить уравнение парной линейной регрессии для данных табл. 2.1, где Y - расходы на покупку продовольственных товаров, % от общих расходов и Х - среднедневная зарплата, руб./чел.×сут. Таблица 2.1 |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 761. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 2. Парный регрессионный анализ
2. Парный регрессионный анализ = bo +b1x.
= bo +b1x.
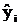 , определяемых регрессией (2.2):
, определяемых регрессией (2.2):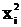 = å xi yi.
= å xi yi.
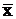 ,
,  ):
):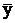 - b1
- b1 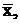 b1 =
b1 = 
 = å
= å  /n - (
/n - ( 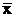 )2.
)2.
 - выборочная ковариация:
- выборочная ковариация: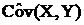 = å xi yi /n -
= å xi yi /n - 
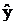 при увеличении х на одну единицу.
при увеличении х на одну единицу.