Списки и их представление на Прологе.

5.3.1.  Основные определения.

В языках, предназначенных для программирования задач искусственного интеллекта, важную роль играют динамические структуры данных, называемые списками. Главное достоинство списков состоит в том, что при их обработке операции вставки, замены и удаления элементов выполняются весьма просто. Списки ¾ структуры данных с последовательным доступом, и поэтому основным средством их обработки является рекурсия.  

Список в языке Пролог представляет собой заключенную в квадратные скобки [] последовательность термов, разделенных запятыми:
[<терм₁>,<терм₂>,…<терм_n>]. Список¾ это составной терм или структура, главный функтор которой обозначается символом «.» (точка).

Структура Список может быть представлена в виде так называемой точечной пары ·(H,T), где Н ¾ первый элемент списка, называемый головой списка, а Т ¾ все остальные элементы списка, называемые хвостом списка. Голова списка является термом, а хвост ¾списком.

В языке Пролог список, разделенный на головы и хвост, обозначается следующим образом: [H|T], например [a|[d,b,k,l]]. Возможность разделения списка на голову и хвост играет важную роль в программировании рекурсивных процедур обработки списков.

Число элементов в списке называется длиной списка. Длина списка может динамически изменяться в процессе выполнения запроса. Список, не имеющий ни одного элемента, обозначается [] и называется пустым списком. Длина пустого списка равно нулю. Пустой список нельзя разделить на голову и хвост.

Голова и хвост списка могут быть заполнены константами, числами или символьными термами, например [1|[6,8,12,9]] или [a|[r,t,y,u]].

Голова и хвост списка могут быть переменными, например,
[H|LT], здесь Н¾терм, а LT¾переменная, имеющая значение списка.

Переменные в Прологе не типизированы, и поэтому в процессе доказательства вопроса они могут конкретизироваться значениями любого типа. Естественно, что интерпретатор не контролирует соблюдение типов аргументов предикатов, это должен делать программист.

5.3.2. Унификация списков.

Списки представляют собой частный случай составных термов, и их унификация выполняется по общим правилам унификации составных термов. Списки успешно унифицируются, если они имеют одинаковую длину и соответствующие элементы этих списков попарно успешно сопоставимы.

Примеры унификации списков.
1) ? ¾[a]=[].
     No
Списки имеют разную длину, унификация невозможна, так как [a] является списком из одного элемента, а [] ¾ пустой список.

2) ? ¾[L]=[a].
    L=a
yes

Списки имеют одинаковую длину, переменная L и терм а успешно унифицируются, и переменная L конкретизируется значением а.

3) ? ¾[L]=[a, b, с].
No

Списки имеют разную длину, переменная L обозначает один элемент списка, а другой операнд операции сопоставления является списком из трех элементов.

4) ? ¾[a|L]=[a, b, с].
L=[b,c]

Yes

Унификация успешна, списки имеют одинаковые первые элементы, переменная L, обозначающая хвост первого списка, успешно сопоставляется и конкретизируется значением [b,c], списком, который является хвостом второго списка.

5.3.3.  Предикат list.

Предикат list(X) во многих версиях языка Пролог является предопределенным предикатом и предназначен для распознавания, является ли терм X списком или нет.

Декларативное описание этого отношения имеет следующий вид:
Для любого X предикат list(X) будет истинен, если X ¾пустой список или выделенный из Х хвост является списком.

Для того, чтобы проверить, является ли  X списком, нужно разделить Х на голову и хвост и убедится, что хвост является списком. Процедура list(X) ¾ рекурсивна. При каждом рекурсивном обращении к процедуре list длина списка уменьшается, успешное завершение рекурсии наступит тогда, когда хвост очередного списка станет пустым. Правило для пустого списка является условием завершения рекурсии, так как пустой список есть список.

Процедура list имеет вид:

list(L):¾[].
list(L):¾L=[H|T],list(T).
Переменная H во втором правиле может быть заменена анонимной переменной, так как ее значение не используется. Более компактная запись процедуры list имеет вид:

list([]).
list([H|T]): ¾ list(T).

Рассмотрим пример запроса к процедуре list.

? ¾ list([1,2,3]).

ТР: list([1,2,3]).

Шаг 1: ТЦ:     list([1,2,3]).

    Пр1: []=[1,2,3]. Þ неуспех

    Пр2: [1|[2,3]]=[_|T1] ÞT1=[2,3]

ТР: list([2,3]).

Шаг 2: ТЦ:     list([2,3]).

    Пр1: []=[2,3]. Þ неуспех

    Пр2: [2|[3]]=[_|T1] ÞT1=[3]

ТР: list([3]).

Шаг 3: ТЦ:     list([3]).

    Пр1: []=[3]. Þ неуспех

    Пр2: [3|[]]=[_|T1] ÞT1=[]

ТР: list([]).

Шаг 4: ТЦ:     list([]).

    Пр1: []=[]. Þ успех

Переход на шаг 3. Истинность ТЦ на шаге 4 влечет истинность цели на шаге 3 list([3]).

Переход на шаг 2. Истинность ТЦ на шаге 3 влечет истинность цели на шаге 2 list([2,3]).

Переход на шаг 1. Истинность ТЦ на шаге 2 влечет истинность цели на шаге 1 list([1,2,3]).

ТР: ÿ ¾успех.

Результат вычисления запроса list([1,2,3]. Þ успех.

Типовые процедуры обработки списков на языке Пролог.

5.4.1. Предикат length.

Предикат определения длины списка length(L,N) является предопределенным предикатом во многих системах программирования на языке Пролог. Схема отношения этого предиката имеет вид:

length(<список>,<длина списка>).

Декларативное описание предиката length(L,N) формулируется следующим образом:   

Предикат length(X, 0) будет истинным, если X ¾пустой список, т.е. длина пустого списка равна нулю. Если список можно разделить на голову и хвост, то длина списка равна длине хвоста списка плюс 1.

Процедура length(L,N) состоит из двух правил:

length([],0).

length([_|T],N):¾length(T,N1),N is N1+1.

Рассмотрим пример запроса к процедуре length.

? ¾ length([1,2,3], N).

ТР: length([1,2,3], N).

Шаг 1: ТЦ:     length([1,2,3], N).

    Пр1: []=[1,2,3]. Þ неуспех

    Пр2: [1|[2,3]]=[_|T11] ÞT11=[2,3]

ТР: length([2, 3], N11),N is N11+1.

Шаг 2: ТЦ:     length([2, 3], N11).

    Пр1: []=[2,3]. Þ неуспех

    Пр2: [2|[3]]=[_|T12] ÞT12=[3]

ТР: length([3], N12),N11 is N12+1,N is N11+1.

Шаг 3: ТЦ:     length([3]).

    Пр1: []=[3]. Þ неуспех

    Пр2: [3|[]]=[_|T13] ÞT13=[]

ТР: length([], N13),N12 is N13+ 1,N11 is N12+1,N is N11+1.

Шаг 3: ТЦ:     length([], N13).

    Пр1: []=[]. Þ успех

{N13=0}

ТР: N12 is N13+ 1,N11 is N12+1,N is N11+1.

Шаг 4: ТЦ:     N12 is 0+ 1.

{N12=1}

ТР: N11 is N12+1,N is N11+1.

Шаг 4: ТЦ:     N11 is 1+ 1.

{N11=2}

ТР: N is N11+1.

Шаг 4: ТЦ:     N is 2+ 1.

{N=2}

ТР: ÿ.

Успех.

Ответ: {N=2}

Предикат member.

Предикат member(X,Y) определяет, принадлежит ли терм Х списку Y. Схема отношения этого предиката имеет вид:

member(<терм>,<список>).

Декларативное описание предиката member формулируется следующим образом:   

Любой терм X принадлежит списку Y, если терм Х является головой списка Y или Х принадлежит хвосту списка Y. В этих двух случаях значение предиката member(X,Y) будет истинным.

Процедура member(X,Y) состоит из двух правил:

member(X,[X|_]).

member(X,[_|T]):¾ member(X,T).

Рассмотрим пример запроса к процедуре member.

? ¾ member(3,[1,2,3,4]).

ТР: member(3,[1,2,3,4]).

Шаг 1: ТЦ:     member(3,[1,2,3,4]).

    Пр1: member(3,[1|[2,3,4]]) Þ неуспех (3 не сопоставимо с 1)

    Пр2: member(3,[1|[2,3,4]]):¾ member(3,[2,3,4]).

ТР: member(3,[2,3,4]).

Шаг 2: ТЦ:     member(3,[2,3,4]).

    Пр1: member(3,[2|[3,4]]) Þ неуспех (3 не сопоставимо с 2)

    Пр2: member(3,[2|[3,4]]):¾ member(3,[3,4]).

ТР: member(3,[3,4]).

Шаг 3: ТЦ:     member(3,[3,4]).

Пр1: member(3,[3|[4]]) Þ успех (3 сопоставимо с 3)

Переход на шаг 2. Истинность ТЦ на шаге 3 влечет истинность цели на шаге 2 member(3,[2,3,4]).

Переход на шаг 1. Истинность ТЦ на шаге 2 влечет истинность цели на шаге 1  member(3,[1,2,3,4]).

ТР: ÿ ¾успех.

Результат вычисления запроса member(3,[1,2,3,4]). Þ успех.

5.4.3. Предикат first.

Предикат first(X,Y) определяет, является ли терм Х первым элементом списка Y. Схема отношения этого предиката имеет вид:

first(<терм>,<список>).

Декларативное описание предиката first формулируется следующим образом:
Терм X является головой списка Y, если терм Х сопоставим с первым элементом списка Y.

Процедура first(X,Y) состоит из факта:

first(X,[X|_]).

5.4.4. Предикат last.

Предикат last(X,Y) определяет, является ли терм Х последним элементом списка Y. Схема отношения этого предиката имеет вид:

last(<терм>,<список>).

Декларативное описание предиката last формулируется следующим образом:   

Если список Y включает только один элемент, и этот элемент сопоставим с термом X, то предикат last(X,Y) истинен. Если список Y можно разделить на голову и непустой хвост и терм Х является последним элементом хвоста списка Y, то предикат last(X,Y) истинен. Если терм Х отсутствует в списке Y, то значение предиката last(X,Y) ¾ложь.

Процедура last(X,Y) состоит из двух правил:

last(X,[Y|[]]):¾X=Y.

last(X,[Z|T]):¾last(X,T).

Рассмотрим пример запроса к процедуре last.

? ¾ last(4,[1,2,3,4]).

ТР: last(4,[1,2,3,4]).

Шаг 1: ТЦ:     last(4,[1,2,3,4]).

    Пр1: last(4,[1|[2,3,4]]) Þ неуспех ([2,3,4] не сопоставим с [])

    Пр2: last(4,[1|[2,3,4]]):¾ last(4,[2,3,4]).

ТР: last(4,[2,3,4]).

Шаг 2: ТЦ:     last(4,[2,3,4]).

    Пр1: last(4,[2|[3,4]]) Þ неуспех ([3,4] не сопоставим с [])

    Пр2: last(4,[2|[3,4]]):¾ last(4,[3,4]).

ТР: last(4,[3,4]).

Шаг 3: ТЦ:     last(4,[3,4]).

Пр1: last(4,[3|[4]]) Þ неуспех ([4] сопоставим с [])

ТР: last(4,[4]).

Шаг 4: ТЦ:     last(4,[4]).

Пр1: last(4,[4|[]]) Þ успех ([] сопоставим с [])

Переход на шаг 3. Истинность ТЦ на шаге 4 влечет истинность цели на шаге 3 last(4,[3,4]).

Переход на шаг 2. Истинность ТЦ на шаге 3 влечет истинность цели на шаге 2 last(4,[2,3,4]).

Переход на шаг 1. Истинность ТЦ на шаге 2 влечет истинность цели на шаге 1 last(4,[1,2,3,4]).

ТР: ÿ.

Результат вычисления запроса last(4,[1,2,3,4]) Þ успех.

5.4.5. Предикат next.

Предикат next(X,Y,L) принимает значение “истина”, если терм Х непосредственно следует за термом Y в списке L. Схема отношения этого предиката имеет вид:

next(<терм>,<терм>,<список>).

Декларативное описание предиката next формулируется следующим образом:   

Если в списке L первые два элемента ¾ X и Y, то предикат next(X,Y,L) истинен, иначе предикат next(X,Y,L) истинен, если термы Х и Y являются первыми элементами хвоста списка L.

Процедура next(X,Y,L) состоит из двух правил:

next(X,Y,[X,Y|L]).

next(X,Y,[U|L]):¾next(X,Y,L).

Рассмотрим пример запроса к процедуре next(X,Y,L).

? ¾ next(2,3,[1,2,3,4]).

ТР: next(2,3,[1,2,3,4]).

Шаг 1: ТЦ:     next(2,3,[1,2,3,4]).

Пр1: next(2,3,[1,2|[3,4]]) Þ неуспех (2 не сопоставимо с 1, 3 не  сопоставимо с 2)

    Пр2: next(2,3,[1|[2,3,4]):¾ next(2,3,[2,3,4]).

ТР: next(2,3,[2,3,4]).

Шаг 2: ТЦ:     next(2,3,[2,3|[3,4]).

Пр1: next(2,3,[2,3|L)(4,[2|[3,4]]) Þ успех (2 сопоставимо с 2, 3     сопоставимо с 3)

ТР: ÿ.

Переход на шаг 1, Истинность ТЦ на шаге 2 влечет истинность цели на шаге 1 next(2,3,[1,2,3,4]).

Результат вычисления запроса: next(2,3,[1,2,3,4]). Þ успех.

5.4.6. Предикат append.

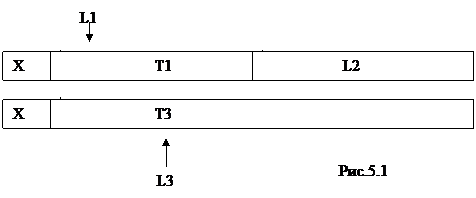
Предикат append(L1,L2,L3) принимает значение “истина”, если список L3 получается путем приписывания все элементов списка L2 после последнего элемента списка L1, как показано на рисунке 5.1. Схема отношения этого предиката имеет вид:

append(<список>,<список,<список>).

Декларативное описание предиката append формулируется следующим образом:   

При присоединении к пустому списку любого списка результирующий список будет идентичен присоединенному списку. Если первый список не пуст, то он разделяется на голову X и хвост T1, а результирующий список L3 =[X|T3] , где Т3 результат присоединения списка L2 к списку Т1.

Процедура append(L1,L2,L3) состоит из двух правил:

append([],L,L).

append([X|T1],L2,[X|T3]):¾append(T1,L2,T3).

Рассмотрим пример запроса к процедуре append(X,Y,L).

? ¾ append([2,3],[1,4],L3).

ТР: append([2,3],[1,4],L3).

Шаг 1: ТЦ:     append([2,3],[1,4],L3).

Пр1: [2,3] не сопоставим [] Þ неуспех

    Пр2: append([2|[3]],[1,4],[2|T31):¾ append([3],[1,4],T31).

     где L3=[2|T31].

ТР: append([3],[1,4],T31).

Шаг 2: ТЦ:     append([3],[1,4],T31).

Пр1: [3] не сопоставим []Þ неуспех

Пр2: append([3|[]],[1,4],[3|T32]):¾ append([],[1,4],T32).

где T31=[3|T32].

Шаг 3: ТЦ:     append([],[1,4],T32).

Пр1: [] сопоставим []Þ успех

Получается подстановка {T32=[1,4]}.

Переход на шаг 2, и конкретизация переменной T31 значением [3|[1,4]] или [3,1,4].

Переход на шаг 1, и конкретизация переменной L3 значением [2|[3,1,4]] или [2,3,1,4].

ТР: ÿ.

Результат вычисления запроса: append([2,3],[1,4],L3).Þ успех при подстановке {L3=[2,3,1,4]}.

5.4.7. Предикат add.

Предикат add(X,Y,Z) истинен, если список Z получается добавлением терма Х в начало списка Y. Схема отношения этого предиката имеет вид:

add(<терм>,<список>,<список>).

Декларативное описание предиката add формулируется следующим образом:
Терм X является головой списка Z, а список Y ¾ хвостом списка Z.

Процедура add(X,Y,Z) состоит из факта:

add(X,Y,[X|Y]).

5.4.8. Предикаты revers1 и revers2.

Предикаты revers1 и revers2 являются предикатами обращения списков и определяют одно и то же отношение различными способами. Схема отношения этого предиката имеет вид:

revers(<список>,<список>).

Предикат revers(X,Y) истинен, если список Y содержит все элементы списка Х, которые записаны в списке Y в обратном порядке. Перестановку элементов списка в обратном порядке можно произвести путем многократного выполнения процедуры append.

Процедура revers определяется двумя способами:

v простым обращением;

v обращением с накоплением.

Простое обращение выполняется процедурой revers1, которая использует процедуру append (см. 5.4.5) и состоит из двух предложений:

revers1([],[]).

revers1([H|Xs],Zs):¾revers1(Xs,Ys), append(Ys,[H],Zs).

Декларативное определение предиката revers1 формулируется следующим образом:

v обращенный пустой список есть пустой список;

v если список Х можно разделить на голову Н и хвост Xs, то Zs есть обращенный список, если Ys ¾обращенный хвост списка X, Zs получен путем присоединения к Ys головы Н списка X.

Рассмотрим пример запроса к процедуре revers1(X,Y).

? ¾ revers1([1,2,3],Zs).

ТР: revers1([1,2,3],Zs).

Шаг 1: ТЦ:     revers1([1,2,3],Y).

Пр1: [1,2,3] не сопоставим [] Þ неуспех

    Пр2: revers1([1|[2,3]],Zs):¾ revers1(Xs1,Ys1),append(Ys1,[1],Zs).

    Xs1=[2,3]

ТР: revers1([2,3],Ys1),append(Ys1,[1],Zs).

Шаг 2: ТЦ:     revers1([2,3],Ys1).

Пр1: [2,3] не сопоставим []Þ неуспех

Пр2: revers1([2|[3]],Ys1):¾ revers1(Xs2,Ys2),append(Ys2,[2],Ys1).

где Xs2=[3].

ТР: revers1([3],Ys2),append(Ys2,[2],Zs).

Шаг 3: ТЦ:     revers1([3],Ys2).

Пр1: [3] не сопоставим []Þ неуспех

Пр2: revers1([3|[]],Ys2):¾revers1(Xs3,Ys3),append(Ys3,[3],Ys2).

где Xs3=[].

ТР: revers1([],Ys3),append(Ys3,[3],Ys2).

Шаг 4: ТЦ:     revers1([],Ys3).

Пр1: [] сопоставим []Þ успех

Получается подстановка {Ys3=[]}.

ТР: append(Ys3,[3],Ys2).

Шаг 5: ТЦ:     append(Ys3,[3],Ys2).

Получается подстановка {Ys2=[3]}.

ТР: append(Ys2,[2],Ys1).

Шаг 6: ТЦ:     append(Ys2,[2],Ys1).

Получается подстановка {Ys1=[3,2]}.

ТР: append(Ys1,[1],Zs).

Шаг 6: ТЦ:     append(Ys1,[1],Zs).

Получается подстановка {Zs=[3,2,1]}.

ТР: ÿ.

Результат вычисления запроса: revers1([1,2,3],Zs). Þ успех

 при подстановке {Zs=[3,2,1]}.

Обращение списка с накоплением выполняется процедурой revers2, состоящей из трех предложений и содержит дополнительный предикат rev:

revers2(X,Y):¾rev(X,[],Y).

       rev([],Y,Y).

rev([H|Xs],L,Y):¾rev(Xs,[H|L],Y).

В процедуре revers2 введен дополнительный предикат rev с тремя аргументами¾списками, где первый аргумент ¾ исходный список, второй аргумент ¾ накапливающийся список, а третий аргумент ¾ результирующий, обращенный список.

Декларативное определение предиката rev формулируется следующим образом:

v если первый аргумент есть пустой список, то второй и третий аргументы представляют собой один и тот же список;

v первый аргумент¾ непустой список [H|Хs], и его можно разделить на голову Н и хвост Xs; в этом случае применение предиката rev к списку [H|Хs] и накапливающемуся списку L равносильно применению предиката rev к хвосту списка Xs и списку [H|L]; при этом получается обращенный список Y.

Рассмотрим пример запроса к процедуре revers2(X,Y).

? ¾ revers2([1,2,3],Y).

ТР: revers2([1,2,3],Zs).

Шаг 1: ТЦ:     revers2([1,2,3],Y).

Пр1: revers2([1,2,3],Y):¾rev([1,2,3],[],Y) Þ успех

    ТР: rev([1,2,3],[],Y).

Шаг 2: ТЦ:     rev([1,2,3],[],Y).

Пр2: [1,2,3] не сопоставим []Þ неуспех

Пр3: rev([1|[2,3]],[],Y):¾ rev(Xs2,[1|[]],Y).

где Xs2=[2,3].

ТР: rev([2,3],[1]],Y).

Шаг 3: ТЦ:     rev([2,3],[1]],Y).

Пр2: [2,3] не сопоставим []Þ неуспех

Пр3: rev([2|[3]],[],Y):¾ rev(Xs3,[2|[1]],Y).

где Xs3=[3].

ТР: rev([3],[2,1],Y).

Шаг 4: ТЦ:     rev([3],[2,1],Y).

Пр2: [3] не сопоставим []Þ неуспех

Пр3: rev([3|[]],[2,1],Y):¾ rev(Xs4,[3|[2,1]],Y).

где Xs4=[].

ТР: rev([],[3,2,1] ,Y).

Пр2: [] сопоставим []Þ успех

Получается подстановка {Y=[3,2,1]}

ТР: ÿ.

Истинность ТЦ на шаге 4 влечет истинность цели на шаге 3.

Истинность ТЦ на шаге 3 влечет истинность цели на шаге 2.

Истинность ТЦ на шаге 2 влечет истинность цели на шаге 1.

Результат вычисления запроса: revers2([1,2,3],Zs) ¾ успех при подстановке {Zs=[3,2,1]}.

5.4.9. Предикат delete.

Предикат delete(X,L,M) принимает значение “истина”, если список M получается в результате удаления первого вхождения терма Х из списка L. Схема отношения этого предиката имеет вид:

delete(<терм>,<список>,<список>).

Декларативное описание предиката next формулируется следующим образом:   

v Если X ¾ голова списка L, то предикат delete(X,L, M) истинен и M есть хвост списка L.

v Если X принадлежит хвосту списка, то предикат delete необходимо применить к хвосту списка L.

v Если X не принадлежит списку L, то предикат delete(X,L, M) ложен.

Процедура delete(X,Y,L) состоит из двух правил:

delete(X,[X|B],B):¾!.

delete(X,[Y|L],[Y|M]):¾ delete(X,L,M).

Рассмотрим пример запроса к процедуре delete(X,Y,L).

? ¾ delete(3,[1,2,3,4],M).

ТР: delete(3,[1,2,3,4],M).

Шаг 1: ТЦ:     delete(3,[1,2,3,4],M).

    Пр1: delete(3,[1|2,3,4]],M) Þ неуспех (3 не сопоставимо с 1)

    Пр2: delete(3,[1|[2,3,4]],[1|M1]):¾ delete(3,[2,3,4],M1).

    M=[1|M1]

ТР: delete(3,[2,3,4],M1).

Шаг 2: ТЦ:     delete(3,[2,3,4],M2).

Пр1: delete(3,[2|[3,4]],M2) Þ неуспех (3 не сопоставимо с 2)

Пр2: delete(3,[2|[3,4]],[2|M2]):¾ delete(3,[3,4],M2).

M1=[2|M2]

ТР: delete(3,[3,4],M2).

Шаг 3: ТЦ:     delete(3,[3,4],M2).

Пр1: delete(3,[3|[4]], M2) Þ успех (3 сопоставимо с 3)

при подстановке M2=[4]

Переход на шаг 2, и конкретизация переменной M1 значением [2|[4]] или [2,4].

Переход на шаг 1, и конкретизация переменной M значением [1|[2,4]] или [1,2,4].

ТР: ÿ.

Результат вычисления запроса: delete(3,[1,2,3,4],M). ¾ успех при подстановке {M=[1,2,4]}.

Предикат number_list.

Предикат number_list(L) определяет, является ли список X списком числовых термов. Схема отношения этого предиката имеет вид:

number_list(<список>).

Декларативное описание предиката number_list(L)формулируется следующим образом:   

v Список L включает один элемент Х. Тогда предикат number_list([X]) истинен, если X числовой терм.

v Список L можно разделить на голову Н и хвост Xs. Тогда L есть список числовых термов, если H ¾числовой терм и хвост списка есть список числовых термов.

Процедура number_list(X,Y) состоит из двух правил:

number_list([]):¾ number(X).

number_list(X,[_|T]): ¾ number(X),number_list(X,T).
Предикат number(X) ¾стандартный предикат системы Arity Prolog, этот предикат истинен, если Х ¾ числовой терм.

Рассмотрим пример запроса к процедуре number_list(Х).

? ¾ number_list([1,2,3,4]).

ТР: number_list([1,2,3,4]).

Шаг 1: ТЦ:     number_list([1,2,3,4]).

    Пр1: [X]=[1,2,3,4] Þнеуспех (списки разной длины)

    Пр2: number_list([1|[2,3,4]]):¾ number(1),number_list([2,3,4]).

ТР: number(1),number_list([2,3,4]).

Шаг 2: ТЦ:     number(1) Þуспех

ТР: number_list([2,3,4]).

Шаг 3: ТЦ: number_list([2,3,4]).

Пр1: [X]=[2,3,4] Þнеуспех (списки разной длины)

    Пр2: number_list([2|[3,4]]):¾ number(2),number_list([3,4]).

ТР: number(2),number_list([2,3,4]).

Шаг 4: ТЦ:     number(2) Þуспех

ТР: number_list([3,4]).

Шаг 5: ТЦ: number_list([3,4]).

Пр1: [X]=[3,4] Þнеуспех (списки разной длины)

    Пр2: number_list([3|[4]]):¾ number(3),number_list([4]).

ТР: number(3),number_list([4]).

Шаг 6: ТЦ:     number(3) Þуспех

ТР: number_list([4]).

Шаг 7: ТЦ: number_list([4]).

Пр1: [X]=[4] Þуспех (списки одинаковой длины) при подстановке {X=4}

ТР: number(4).

 Шаг 8: ТЦ:    number(4) Þуспех

ТР: ÿ ¾успех.

Результат вычисления запроса number_list(3,[1,2,3,4]). Þ успех.

Предикат sumlist.

Предикат sumlist(L,Sum) определяет сумму элементов числового списка. Схема отношения этого предиката имеет вид:

sumlist(<список>,<целочисленный терм>).

Декларативное описание предиката sumlist формулируется следующим образом:   

v Сумма элементов пустого списка равна нулю.

v Если исходный список состоит L из головы Н и хвоста Т, то сумма элементов списка L равна сумме элементов хвоста списка T плюс Н.

Процедура sumlist(L,Sum) состоит из двух правил:

sumlist([],0).

sumlist([H|T],Sum):¾ sumlist(T,SumT),Sum is SumT+H.

Рассмотрим пример запроса к процедуре sumlist.

? ¾ sumlist([1,2,3,4],S).

ТР: sumlist([1,2,3,4],S).

Шаг 1: ТЦ:     sumlist([1,2,3,4],S).

    Пр1: [1,2,3,4]=[] Þ неуспех (списки разной длины)

    Пр2: sumlist([1|[2,3,4]],S):¾ sumlist([2,3,4],ST1), S is ST1+1.

ТР: sumlist([2,3,4],ST1),S is ST1+1.

Шаг 2: ТЦ:     sumlist([2,3,4]).

    Пр1: [2,3,4]=[] Þ неуспех (списки разной длины)

Пр2: sumlist([2|[3,4]],ST1):¾ sumlist([3,4],ST2),ST1 is ST2+2.

ТР: sumlist([3,4],ST2),ST1 is ST2+2, S is ST1+1.

Шаг 3: ТЦ:     sumlist([3,4],ST2).

Пр1: [3,4]=[] Þ неуспех (списки разной длины)

Пр2: sumlist([3|[4]],ST2):¾ sumlist([4],ST3) ,ST2 is ST3+3.

ТР: sumlist([4],ST3),ST2 is ST3+3,ST1 is ST2+2, S is ST1+1.

Шаг 4: ТЦ:     sumlist([4],ST3).

Пр1: [4]=[] Þ неуспех (списки разной длины)

Пр2: sumlist([4|[]],ST4):¾ sumlist([],ST4) ,ST3 is ST4+4.

ТР: sumlist([],ST4),ST3 is ST4+4,ST2 is ST3+3,ST1 is ST2+2,

 S is ST1+1.

Шаг 5: ТЦ:     sumlist([],ST4).

Пр1: []=[]Þ успех при подстановке {ST4=0}

ТР: ST3 is 0+4,ST2 is ST3+2,ST1 is ST2+2, S is ST1+1.

Шаг 6: ТЦ:     ST3 is 0+4. Þ успех при подстановке {ST3=4}

ТР: ST2 is 4+3,ST1 is ST2+2, S is ST1+1.

Шаг 7: ТЦ:     ST2 is 4+3. Þ успех при подстановке {ST2=7}

ТР: ST1 is 7+2, S is ST1+1.

Шаг 8: ТЦ:     ST1 is 7+2. Þ успех при подстановке {ST1=9}

ТР: S is 9+1.

Шаг 8: ТЦ:     S is 9+1. Þ успех при подстановке {S=10}

ТР: ÿ ¾успех.

Результат вычисления запроса sumlist([1,2,3,4],S). Þ успех при подстановке {S=10}.

Предикат delrepeat.

Предикат delrepeat (L,LS) истинен, если список получается из списка S путем удаления всех повторений элементов. Схема отношения этого предиката имеет вид:

delrepeat(<список>,<список>).

Удаление повторений элементов выполняется процедурой delrepeat с накоплением списка, состоящей из четырех предложений и содержит дополнительный предикат delrep:

delrepeat(S,SF):-delrep(S,[],SF).

delrep([],S,S).

delrep([H|T],S1,SF):-member(H,T),!,delrep(T,S1,SF).

delrep([H|T],S1,SF):-append(S1,[H],S2),delrep(T,S2,SF).

Декларативное описание предиката delrep формулируется следующим образом:   

v если первый аргумент есть пустой список, то второй и третий аргументы представляют собой один и тот же список;

v если первый аргумент¾ непустой список [H|Хs], и голова Н принадлежит хвосту списка T, то процедура delrep рекурсивно вызывается с аргументами T и S1; при этом элемент H не включается в накапливающийся список S1;

v если первый аргумент¾ непустой список [H|Хs], и голова Н не принадлежит хвосту списка T, то элемент H включается в накапливающийся список S1 и получается список S2. Затем процедура delrep рекурсивно вызывается с аргументами T и S2.

Процедура delrepeat выполняется следующим образом:

? ¾ delrepeat ([1,1,2,3,2,4,3],S).

ТР: delrepeat ([1,1,2,3,2,4,3],S).

Шаг 1: ТЦ:     delrepeat ([1,1,2,3,2,4,3],S).

Пр1: delrepeat ([1,1,2,3,2,4,3],S):¾ delrep([1,1,2,3,2,4,3],[],S). Þ успех

    ТР: delrep([1,1,2,3,2,4,3],[],S).

Шаг 2: ТЦ:     delrep([1,1,2,3,2,4,3],[],S)

Пр2: [1,1,2,3,2,4,3] не сопоставим []Þ неуспех

Пр3:

delrep([1|[1,2,3,2,4,3]],[],S):¾member(1,[1,2,3,2,4,3]),delrep([1,2,3,2,4,3],[],S).

ТР: member(1,[1,2,3,2,4,3]),delrep([1,2,3,2,4,3],[],S).

Шаг 3: ТЦ:     member(1,[1,2,3,2,4,3]). Þ успех[1]

ТР: delrep([1,2,3,2,4,3],[],S).

Шаг 4: ТЦ:     delrep([1,2,3,2,4,3],[],S).

Пр2: [1,2,3,2,4,3] не сопоставим []Þ неуспех

Пр3:

delrep([1|[2,3,2,4,3]],[],S):¾member(1,[2,3,2,4,3]),delrep([2,3,2,4,3],[],S).

ТР: member(1,[2,3,2,4,3]),delrep([2,3,2,4,3],[],S).

Шаг 5: ТЦ:     member(1,[2,3,2,4,3]). Þ неуспех

Возврат.

Пр4:

delrep([1|[2,3,2,4,3]],[],S):¾append([],[1],S2]),delrep([2,3,2,4,3],S2,S).

ТР: append([],[1],S2]),delrep([2,3,2,4,3],S2,S).

Шаг 6: ТЦ:     append([],[1],S2]). Þ успех[2]

S2=[1]

ТР: delrep([2,3,2,4,3],[1],S).

Шаг 7: ТЦ:     delrep([2,3,2,4,3],[1],S)

Пр2: [2,3,2,4,3] не сопоставим []Þ неуспех

Пр3:

delrep([2|[3,2,4,3]],[],S):¾member(2,[3,2,4,3]),delrep([3,2,4,3],[1],S).

ТР: member(2,[3,2,4,3]),delrep([3,2,4,3],[1],S).

Шаг 8: ТЦ:     member(2,[3,2,4,3]). Þ успех

ТР: delrep([3,2,4,3],[1],S).

Шаг 9: ТЦ:     delrep([3,2,4,3],[1],S).

Пр2: [3,2,4,3] не сопоставим []Þ неуспех

Пр3:

delrep([3|[2,4,3]],[1],S):¾member(3,[2,4,3]),delrep(2,4,3],[1],S).

ТР: member(3,[2,4,3]),delrep([2,4,3],[1],S).

Шаг 10: ТЦ:   member(3,[2,4,3]). Þ успех

Шаг 11: ТЦ:   delrep([2,4,3],[1],S).

Пр2: [2,3,2,4,3] не сопоставим []Þ неуспех

Пр3:

delrep([2|[4,3]],[],S):¾member(2,[4,3]),delrep([4,3],[1],S).

ТР: member(2,[4,3]),delrep([3,2,4,3],[1],S).

Шаг 12: ТЦ:   member(2,[4,3]). Þ неуспех

Возврат.

Пр4:

delrep([2|[4,3]],[],S):¾append([1],[2],S2]),delrep([4,3],S2,S).

ТР: append([1],[2],S2]),delrep([4,3],S2,S).

Шаг 13: ТЦ:   append([1],[2],S2]). Þ успех

S2=[1,2]

ТР: delrep([4,3],[1,2],S).

Пр2: [4,3] не сопоставим []Þ неуспех

Пр3:

delrep([4|[3]],[1,2],S):¾member(4,[3]),delrep([3],[1,2],S).

ТР: member(4,[3]),delrep([3],[1,2],S).

Шаг 14: ТЦ:   member(2,[4,3]). Þ неуспех

Возврат.

Пр4:

delrep([4|[3]],[],S):¾append([1,2],[4],S2]),delrep([3],S2,S).

Шаг 15: ТЦ:   append([1,2],[4],S2]). Þ успех

S2=[1,2,4]

ТР: delrep([3],[1,2,4],S).

Пр2: [3] не сопоставим []Þ неуспех

Пр3:

delrep([3|[]],[1,2,4],S):¾member(3,[]),delrep([],[1,2,4],S).

ТР: member(3,[]),delrep([],[1,2],S).

Шаг 16: ТЦ:   member(3,[]). Þ неуспех

Возврат.

Пр4:

delrep([3|[]],[1,2,4],S):¾append([1,2,4],[3],S2]),delrep([],S2,S).

Шаг 17:ТЦ:    append([1,2,4],[3],S2]). Þ успех

S2=[1,2,4,3]

ТР: delrep([],[1,2,4,3],S).

Шаг 18: ТЦ:   delrep([],[1,2,4,3],S).

Пр2: [] сопоставим []Þ успех

Получается подстановка {S=[1,2,4,3]}

ТР: ÿ.

Результат вычисления запроса: delrepeat ([1,1,2,3,2,4,3],S).¾ успех при подстановке {S=[1,2,4,3]}