Общая схема согласования целевых утверждений.

Самым общим случаем Пролог¾программы является программа, включающая как факты, так и правила. Рассмотрим процесс вычисления запроса на основе такой логической программы. Процесс вычисления начинается с некоторого исходного вопроса Q, который в общем случае может быть конъюнктивным, и завершается получением одного из двух результатов:

· успешного согласования целей вопроса;

· неуспеха (или неудачи).

В случае успешного вычисления мы получаем конкретизацию переменных, входящих в вопрос. Неудача означает невозможность вывода какой-либо цели вопросы из программы.

Допустим, что логическая программа P состоит из фактов и правил, а вопрос Q ¾ конъюнктивный и содержит цели G₁,G₂,…G_n. Интерпретатор языка Пролог будет вычислять ответ на вопрос согласно следующим принципам, на которых он реализован:

· Цели запроса обрабатываются слева направо, G₁ будет согласовываться первой, а G_n ¾последней.

· Предложения программы просматриваются интерпретатором сверху вниз.

· Если цель G_i сопоставима с заголовком правила H_j, то она должна быть сопоставима с предикатами в правой части правила. Интерпретатор заменяет цель G_i на правую часть правила H_j. Это действие называется редукцией. Другими словами, Редукцией цели G с помощью программы P называется замена цели G_i на тело правила C_j, заголовок которого H_j унифицируется с целью G_i. Вычисление вопроса выполняется в виде последовательности редукций, цепочки преобразований исходного вопроса. На каждом этапе вычисления существует некоторая конъюнкция целей (или одна цель), называемая резольвентой. Цели, которые добавляются в запрос в результате редукции, называются производными целями от цели G_i и правила C_j. Если цель G_i сопоставима с заголовком правила H_j, то список целей в запросе увеличивается. 

· Если цель G_i сопоставима с фактом, то конкретизируются переменные этой цели, и общие переменные цели G_i и других целей, входящих в вопрос, затем осуществляется переход к сопоставлению следующей цели G_i+1 , и, таким образом, список целей, подлежащих согласованию уменьшается.

· Когда мы таким образом достигнем последней цели в запросе, и она успешно будет согласована с каким-либо фактом программы, то текущая резольвента окажется пустой, и вычисление запроса будет успешным.

Процедуру Вычислить можно представить более формализовано на языке описания алгоритмов (псевдокоде) в следующем виде:

ПРОЦЕДУРА Вычислить(Прогр, СписокЦелей, ПризнакУспеха)

Входные параметры:
Прогр: список предложений на языке Пролог;
СписокЦелей: запрос;

Выходной параметр:
ПризнакУспеха: истина, если СписокЦелей истинен;
                        ложь, в противном случае.

Локальные переменные:
Цель: предикат;
ДругиеЦели: список целей;
Достигнуты: истинностное значение;
Конкрет: конкретизация переменных;
H, H’, B₁, B₁’, ……B_n,B_n’: цели;

Вспомогательные функции:
пустой(L): возвращает значение «истина», если L ¾пустой список;
голова(L): возвращает первый элемент списка L;
хвост(L): возвращает остальные элемент списка L;
конкат(L1,L2): присоединяет список L2 к концу списка L1;
сопоставление(T1,T2,Сопоставимы, Конкрет): пытается унифицировать термы Т1 и Т2; если они унифицируются, то переменной Сопоставимы присваивается значение “истина”, а Конкрет представляет собой конкретизацию переменных;
подстановка(Конкрет, Цели): производит подстановку переменных в Цели согласно Конкрет;

НАЧАЛО_ПРОЦЕДУРЫ
ЕСЛИ   пустой(СписокЦелей)     ТО ПризнакУспеха=истина

ИНАЧЕ Цель:=голова(СписокЦелей);

ДругиеЦели:=хвост(СписокЦелей);

Достигнуты:=ложь;

ЦИКЛ ПОКА (Достигнуты=ложь И

    “в программе есть еще предложения”)

ЕСЛИ следующее предложение в Прогр есть H:¾B₁,B₂,…B_n.    ТО  создать вариант этого предложения H’:¾ B’₁,B’₂,…B’_n.
    путем переименования переменных;
    сопоставление(Цель, H’, Сопоставимы, Конкрет);

ЕСЛИ   Сопоставимы ТО
НовыеЦели:= конкат([B’₁,B’₂,…B’_n,],ДругиеЦели);

НовыеЦели:=подстановка(Конкрет,НовыеЦели);
Вычислить(Прогр,НовыеЦели,Достигнуты);

КОНЕЦ_ЕСЛИ
КОНЕЦ_ЕСЛИ
ИНАЧЕ найден факт H;

создать вариант этого факта H’
путем переименования переменных;

сопоставление(Цель, H’, Сопоставимы, Конкрет);

ЕСЛИ   Сопоставимы ТО
НовыеЦели:= ДругиеЦели;

НовыеЦели:=подстановка(Конкрет,НовыеЦели);
Вычислить(Прогр,НовыеЦели,Достигнуты);

     КОНЕЦ_ЕСЛИ
КОНЕЦ_ЦИКЛА

КОНЕЦ_ЕСЛИ
ПризнакУспеха:=Достигнуты;

КОНЕЦ_ПРОЦЕДУРЫ

Рассмотрим пример вычисления запроса на основе программы, включающей и факт, и правила. Пусть программа содержит утверждения, приведенные ниже:

big(‘медведь’).        %предложение 1

big(‘слон’).                       %предложение 2

little(‘кот’).                       %предложение 3

little(‘мышь’).          %предложение 4

black(‘кот’).             %предложение 5

grey(‘слон’).            %предложение 6

grey(‘мышь’).          %предложение 7

brown(‘медведь’).            %предложение 8

dark(Z):¾black(Z).  %предложение 9

dark(Z):¾brown(Z). %предложение 10

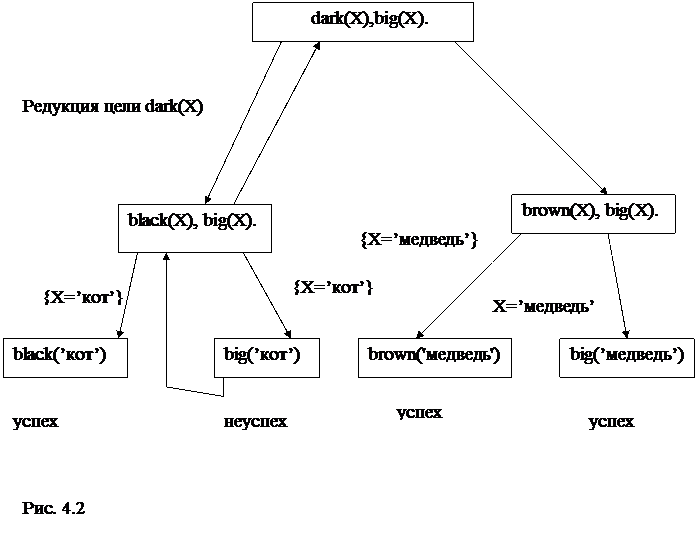
Для вычисления запроса “? ¾ dark(X),big(X). “ интерпретатор выполняется следующие действия:

Шаг 1.  Текущая резольвента Q1 есть исходный запрос ¾ dark(X),big(X).

Шаг 2.  Текущая резольвента Q2 является конъюнкцией целей dark(X),big(X). Выбираем первую цель G21¾dark(X) и, просматривая программу с первого предложения, находим предложение 9, сопоставимое с целью G21, является правилом

dark(Z):¾black(Z). 
переименовываем переменную Z на Х и вместо цели G21 подставляем правую часть правила 9. Получаем текущую резольвенту Q3¾black(X),big(X)

Шаг 3.  Текущая резольвента Q3 является конъюнкцией целей black(X),big(X). Выбираем первую цель G31¾black(X) и, просматривая программу с первого предложения, находим предложение 5, сопоставимое с целью G31, black(‘кот’).
при подстановке {X=’кот’}. Предложение 5 является фактом, поэтому список целей в резольвенте сократится, так как цель G31 удаляется , а в цель G32 при подстановке {X=’кот’} примет вид
big(‘кот’). Получаем текущую резольвенту Q4: big(‘кот’).

Шаг 4   Текущая резольвента Q4 включает одну цель G41 big(‘кот’). Просматривая программу с первого предложения, не находим ни одного предложения, сопоставимого с целью G41,
поэтому выполняется возврат на шаг 3.

Шаг 3.  Текущая резольвента Q3 является конъюнкцией целей black(X),big(X). Выбираем первую цель G31¾black(X) и, просматривая программу с предложения 6 до конца программы, и  не находим ни одного предложения 5, сопоставимого с целью G31, поэтому выполняется возврат на шаг 2.

Шаг 2.  Текущая резольвента Q2 является конъюнкцией целей dark(X),big(X). Выбираем первую цель G21¾dark(X) и, просматривая программу с предложения 10, находим предложение 10, сопоставимое с целью G21, является правилом

dark(Z):¾brown(Z).
переименовываем переменную Z на Х и вместо цели G21 подставляем правую часть правила 9. Получаем текущую резольвенту Q5¾ brown (X),big(X).

Шаг 5.  Текущая резольвента Q5 является конъюнкцией целей brown(X),big(X). Выбираем первую цель G51¾ brown(X) и, просматривая программу с первого предложения, находим предложение 8, сопоставимое с целью G51, brown(‘медведь’).
при подстановке {X=’медведь’}. Предложение 8 является фактом, поэтому список целей в резольвенте сократится, так как цель G51 удаляется , а в цель G52 при подстановке {X=’медведь’} примет вид
big(‘медведь’). Получаем текущую резольвенту Q6: big(‘медведь’).

Шаг 6   Текущая резольвента Q6 включает одну цель G61 big(‘медведь’). Просматривая программу с первого предложения, находим предложение 1, сопоставимое с целью G61,
которое является фактом, поэтому цель G61 удаляется из текущей резольвенты, и она становится пустой, Q7=ÿ.

Шаг 7.  Текущая резольвента Q7 есть пустой дизъюнкт, это указывает на успешное завершение вычисления запроса Q1. Интерпретатор выдает конкретизацию переменной {X=’медведь’} как результат вычисления запроса.

Процесс вычисления запроса удобно представить в виде дерева поиска. Дерево поиска ответа на любой запрос строится следующим образом.

· Корнем дерева является исходный вопрос Q.

· Вершины дерева соответствуют целям (резольвентам), которые в общем случае являются конъюнктивными. В каждой выделяется одна цель.

· Для каждого утверждения программы, заголовок которого унифицируется с выделенной в вершине целью имеется ребро, выходящее из этой вершины.

· На ребрах дерева записываются подстановки, которые образуются в результате унификации выделенной в вершине цели и утверждения.

· Лист дерева называется успешной вершиной, если существует подстановка, удовлетворяющая последнюю цель в списке целей. Лист дерева называется безуспешной вершиной, если нет в программе утверждений, которые сопоставимы с выделенной в вершине целью.

Рассмотрим пример построения дерева поиска для запроса: dark(X),big(X).

Когда выполнение программы достигает тупиковой вершины, отмеченной словом "неуспех", автоматически происходит возврат на предыдущий уровень дерева поиска, так как в Пролог¾систему встроен механизм возврата (backtracing). Выполнение алгоритм поиска решения можно представить как обход лабиринта, где на каждой развилке приходится выбирать новый путь. При попадании в тупик, т.е. на безуспешную вершину (лист дерева поиска), надо следовать в обратном направлении до первого перекрестка, и выбирать другой не опробованный путь, Процесс продолжается до тех пор, пока не встретится успешная вершина или будут пройдены все пути дерева поиска.

В вычислительной модели языка Пролог приняты правила просмотра целей в запросе слева направо и поиска сопоставимых правил и фактов в программе сверху вниз. Такой принцип поиска называется поиском в глубину. Рассмотрим теперь механизм поиска с возвратом.