
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
В прямоугольной системе координатСтр 1 из 3Следующая ⇒ ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Двойной интеграл Определение и свойства двойного интеграла
Определение 1: Пусть в замкнутой области В i-й частичной области Составим аналогичные произведения по всем частичным областям
Сумма (1) называется интегральной суммой для функции Обозначим через Если при стремлении к нулю Отметим достаточные условия существования двойного интеграла. Теорема 1(достаточные условия существования двойного интеграла): Если в замкнутой ограниченной области Свойства

где
Вычисление двойных интегралов в прямоугольной системе координат Пусть требуется найти значение двойного интеграла.
Определение: Плоская область Покажем, что, если область Найдем объем, воспользовавшись формулой вычисления объема по известным площадям поперечных сечений
Будем считать, что Проведем перпендикулярную оси ОХ плоскость, которая пересечет данное тело по некоторой криволинейной трапеции Тогда С другой стороны,
Интеграл, стоящий в правой части (1) – повторный; a и b – внешние пределы интегрирования (они всегда постоянны), Для расстановки пределов интегрирования в двойном интеграле достаточно изобразить в Порядок интегрирования можно изменить: внутренний интеграл вычислить по переменной Тогда
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
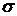 плоскости
плоскости  определена функция
определена функция  . Разобьем область
. Разобьем область  , площади которых обозначим
, площади которых обозначим  .
. , возьмем произвольную точку
, возьмем произвольную точку 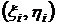 и значение функции в данной точке
и значение функции в данной точке  умножим на площадь
умножим на площадь  этой области.
этой области. и, просуммировав полученные произведения, будем иметь
и, просуммировав полученные произведения, будем иметь (1).
(1). наибольший из диаметров частичных областей
наибольший из диаметров частичных областей  .
. . Двойной интеграл не зависит от обозначения переменных интегрирования.
. Двойной интеграл не зависит от обозначения переменных интегрирования. . Постоянный множитель можно выносить за знак двойного интеграла
. Постоянный множитель можно выносить за знак двойного интеграла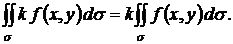
 . Двойной интеграл от суммы двух (и более) функций равен сумме двойных интегралов от слагаемых
. Двойной интеграл от суммы двух (и более) функций равен сумме двойных интегралов от слагаемых
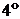 . Если область
. Если область  и
и  то
то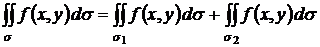 .
.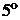 . Если всюду в области
. Если всюду в области  , то
, то  .
. Если в области
Если в области  , то
, то  .
. . Если функция
. Если функция  .
. .
. 
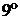 . (Теорема о среднем): Если функция
. (Теорема о среднем): Если функция  , такая что
, такая что .
. . Если функция
. Если функция  ,
, площадь области
площадь области  - наименьшее, а
- наименьшее, а  - наибольшее значения функции
- наибольшее значения функции 
 (рис. 1), если любая прямая, параллельная оси
(рис. 1), если любая прямая, параллельная оси  .
.

 (рис.2). Точки А и В разделяют
(рис.2). Точки А и В разделяют  и АNB, ее уравнение
и АNB, ее уравнение  .
. . Площадь сечения
. Площадь сечения  зависит от
зависит от  и может быть вычислена с помощью определенного интеграла
и может быть вычислена с помощью определенного интеграла  .
. .
. , получаем формулу
, получаем формулу (1).
(1). и
и  – внутренние пределы интегрирования (они могут быть как постоянными, так и переменными). Вначале вычисляется внутренний интеграл, при этом вторая переменная (для записанной формулы -
– внутренние пределы интегрирования (они могут быть как постоянными, так и переменными). Вначале вычисляется внутренний интеграл, при этом вторая переменная (для записанной формулы -  область интегрирования
область интегрирования 
 . Допустим, что область
. Допустим, что область  , уравнение линии NAK
, уравнение линии NAK  ; NBK -
; NBK -  .
. .
.