
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнение средних значений двух выборок.Имеем две выборочные совокупности: X{x1, x2, … xn1}иY{y1, y2, … yn2} n1 –объём первой выборки, n2– объём второй выборки. Н0: М[X]=M[Y] или M[X]-M[Y]=0, т.е. обе выборки принадлежат одной генеральной совокупности, то есть различия между выборками не достоверны. Задаём уровень значимости ά.
Число степеней свободы Если
Находим из таблицы критерия Стьюдента для если Вывод: обе выборки принадлежат одной генеральной совокупности, различия между выборками не достоверны. если Вывод: обе выборки не принадлежат одной генеральной совокупности, различия между выборками достоверны.
Непараметрические критерии. Непараметрические критерии сравнивают сами значения выборок (варианты), они используют ранги. Ранг -- это место по возрастанию. Если встречается несколько одинаковых значений, то их ранг = среднему арифметическому рангов. Число рангов=n -- количество значений для которых расставляем ранги. Пример:
Критерий Вилкоксона. Работает с так называемыми сопряжёнными вариантами, когда варианты из двух выборок измеряются парами (например, значению xi до воздействия препарата соответствует yi после воздействия). Итак, имеем две выборки одинакового объёма n1=n2=n : X{x1, x2, … xn}– контроль Y{y1, y2, … yn}– опыт Нас интересует достоверно ли различие между выборками, то есть принадлежат ли XиY одной генеральной совокупности для заданного уровня значимости ά.  Алгоритм проверки статистической гипотезы: 1). Н0: различие между выборками не достоверно. 2). Вычислить разности: 3). Расставить ранги для разностей, знак разности не учитываем. То есть расставляем ранги для 4). Подсчитать суммы рангов, учитывая знаки разностей: R+ -- сумма рангов для R- -- сумма рангов для 5). 6).Определить по таблице критерия Вилкоксона для α и числа степеней свободы=n Тэксп. 7). Если Тэксп ≤Ткрит то Н0 отвергаем. если Тэксп>Ткрит то Н0 принимаем. 8). Записать вывод. Пояснения: считается, что если различия между выборками не достоверны, (то есть верна гипотеза Н0), то R+и R-не сильно отличаются друг от друга. В таблице содержатся критические значения для меньшей суммы рангов и если Тэксп<Ткрит , то различия велики и гипотезу Н0 следует отвергнуть. Пример: Достоверны ли различия между выборками для уровня значимости α=0,05? Н0: Различия между выборками не достоверны.
n=9-1=8 R-=1+2,5=3,5 R+=7+8+2,5+6+5+4=32,5 Следовательно Тэксп=3,5. По таблице для n=8 и α=0,05 находим: Ткрит=4.
Вывод: Различия между выборками достоверны.
Критерий Манна-Уитни. Этот непараметрический критерий можно использовать для двух выборок как одинаковых, так и разных объёмов. Объём меньшей выборки обозначают n1. То есть, если Обе выборки объединяют в один ряд и ранги расставляют для всех n1+ n2 чисел.
Алгоритм проверки статистической гипотезы: 1). Н0: различие между выборками не достоверно. 2). Расставить ранги для всех n1+ n2 значений. 3). Вычислить:
где 4) . 5). а). Если если если в). Если Если Uэксп ≤Uкрит то Н0 отвергаем. если Uэксп˃Uкрит то Н0 принимаем. 6). Записать вывод.
Пример: даны две выборки. По критерию Манна-Уитни проверить, достоверны ли различия между выборками для уровня значимости α=0,05?
Н0: Различия между выборками не достоверны. n1+ n2 =4+5=9 R1=1+3+4+6=14 R2=2+5+7+8+9=31
В таблице для n2=5,находим для n1=4 и
Вывод: Различия между выборками не достоверны. Контрольные вопросы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 493. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
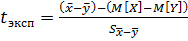
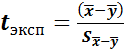
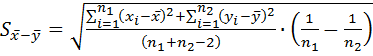
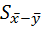 ошибка разности средних арифметических
ошибка разности средних арифметических 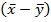 .
.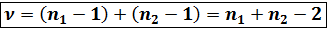
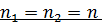 ,
, 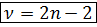
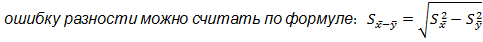
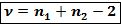 и заданного ά,
и заданного ά, 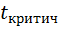 .
.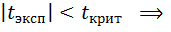 Н0 принимаем
Н0 принимаем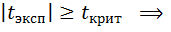 Н0 отвергаем
Н0 отвергаем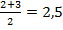
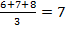
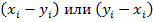 . Если
. Если 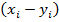 =0, то i-ю строку вычеркнуть и n=n-k -- количество вычеркнутых строк.
=0, то i-ю строку вычеркнуть и n=n-k -- количество вычеркнутых строк.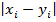 .
.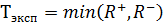 , то есть выбираем меньшее из двух чисел.
, то есть выбираем меньшее из двух чисел.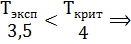 Н0 отвергаем.
Н0 отвергаем.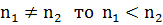 .
.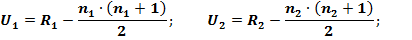
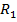 -- сумма рангов для первой выборки,
-- сумма рангов для первой выборки,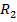 -- сумма рангов для второй выборки.
-- сумма рангов для второй выборки.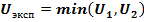
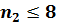 ,то в таблице для
,то в таблице для 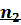 по
по 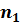 и
и 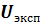 находим число -- это вероятность гипотезы Н0: Р(Н0).
находим число -- это вероятность гипотезы Н0: Р(Н0).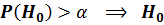 принимаем,
принимаем,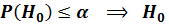 отвергаем. Где α -- заданный уровень значимости.
отвергаем. Где α -- заданный уровень значимости.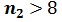 ,то существует другая таблица. В ней для
,то существует другая таблица. В ней для 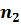 находим
находим 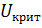 .
.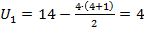
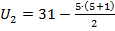 =16
=16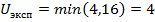
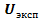 =4:
=4: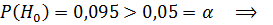 Н0 принимаем.
Н0 принимаем.