
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные этапы проверки статистических гипотез.Стр 1 из 4Следующая ⇒ Проверка статистических гипотез.
Статистическая гипотеза -- это предположение о генеральной совокупности, высказанное на основании статистических выборочных данных. Статистическая проверка гипотез -- это процедура обоснованного сопоставления высказанной гипотезы с имеющимися выборочными данными. Например: исследуем влияние нового лекарственного препарата на снижение артериального давления. X{x1, x2, … xn1} -- контрольная группа (выборка, объёмом n1) Y{y1, y2, … yn2} -- опытная группа (выборка объёмом n2) Высказываются две альтернативные гипотезы: Н0: -- различия между выборками не достоверны (т.е. носят случайный характер). Н: -- различия между выборками достоверны (т.е. влияние препарата достоверно (эффективно)) Чтобы принять или опровергнуть эти предположения, используют статистические критерии или критерии достоверности. Статистический критерий -- это случайная величина, закон распределения которой известен, т.е. каждому значению критерия поставлена в соответствие вероятность, с которой он эти значения принимает. Для каждого критерия существует таблица, в которой содержатся критические значения критерия. Каждое критическое значение соответствует определённому уровню значимости α и числу степеней свободы
α=1-РД -- это вероятность принять ошибочную гипотезу. Критические значения позволяют определить вероятность нулевой гипотезы: Р(Н0). Гипотеза Н0 принимается, если в результате проверки выяснилось, что её вероятность больше выбранного уровня значимости. если Р(Н0)>α , то Н0 принимаем,  если Р(Н0)<α , то Н0 отвергаем. Например: Хотим доказать достоверность различия между выборками X{x1, x2, … xn1}иY{y1, y2, … yn2} с РД=0,95 (это значит, что влияние препарата достоверно (эффективно) на 95%). Если в результате проверки выяснилось, что Р(Н0)˃α , (т.е. ˃0,05), то мы вынуждены принять гипотезу Н0, так как Р(Н)<РД Р(Н)<0,95.
Основные этапы проверки статистических гипотез. 1).Выдвигается гипотеза Н0. 2).Выбирается величина уровня значимости α (α=1-РД). 3).По заданному α и числу степеней свободы ν(или к) в таблице находим критическое (табличное) значение критерия. 4).Подсчитывается экспериментальное значение критерия по имеющимся выборкам (для каждого критерия существует формула для определения значения критерия). 5).С помощью сравнения экспериментального и критического значений делается вывод о правомерности гипотезы Н0. 6).Если Н0 принимается, следовательно гипотеза Н (о достоверности различий) не верна. Если Н0 отвергается, следовательно верна гипотеза Н..(Н0 и Н -- противоположные события). Критерии достоверности подразделяются на параметрические и непараметрические. Параметрическиекритерии для вычисления экспериментального значения используют статистические параметры: Непараметрические критерии не требуют вычисления выборочных параметров, они менее точны, дают более грубую оценку, чем параметрические критерии, но: 1). Их можно применять к выборкам, закон распределения которых неизвестен (не обязательно нормальное распределение). 2). Они проще и позволяют быстрее производить проверку рассматриваемых гипотез. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 539. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
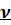 (или к)
(или к)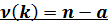 где а -- число наложенных связей или ограничений.
где а -- число наложенных связей или ограничений.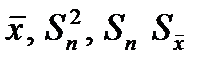 . Они могут использоваться для выборочных совокупностей, распределённых по закону близкому к нормальному (Гаусса).
. Они могут использоваться для выборочных совокупностей, распределённых по закону близкому к нормальному (Гаусса).