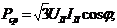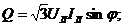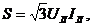Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СОЕДИНЕНИЯ ПРИЕМНИКОВ ЗВЕЗДОЙИз рисунке 6 видно, что при соединении звездой фазные напряжения приемника Ua, Ub и Uc не равны линейным напряжениям Uab, Ubc и Uca. Применяя второй закон Кирхгофаи к контурам aNba, bNcb и cNac, можно получить следующие соотношения между линейными и фазными напряжениями:
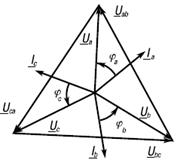
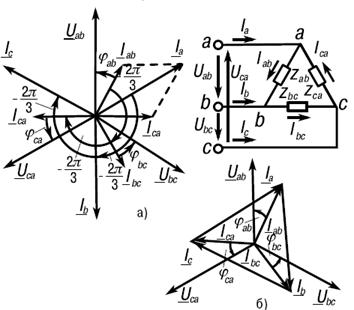
. Нетрудно построить векторы линейных напряжений (рис. 7).
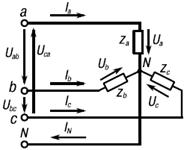
Рис. 6. Схема соединения приемника звездой
Рис. 7. Векторная диаграмма при соединении приемника звездой в случае симметричной нагрузки Если не учитывать сопротивлений линейных проводов и нейтрального провода, то следует считать комплексные значения линейных и фазных напряжений приемника равными, соответственно, комплексным значениям линейных и фазных напряжений источника. Вследствие указанного равенства векторная диаграмма напряжений приемника не отличается от векторной диаграммы источника при соединении звездой (см. рис.7). Линейные и фазные напряжения приемника, как и источника, образуют две симметричные системы напряжений. Между линейными и фазными напряжениями приемника существует соотношение Uл=√3Uф. Основным стандартным линейным (между фазными проводами) напряжением для низковольтных сетей (до 1000 В) принимается напряжение 380 В, при этом фазное напряжение (между фазным проводом и центральным) будет составлять (380/√3) = 220 В. Из схемы рисунке 6 видно, что при соединении звездой линейные токи равны соответствующим фазным токам: Iд = Iф. С помощью первого закона Кирхгофаполучим следующее соотношение между фазными токами и током нейтрального провода:
Соединение приемников треугольником Как видно из схемы, каждая фаза приемника при соединении треугольником подключена к двум линейным проводам. Поэтому независимо от значения и характера сопротивлений приемника каждое фазное напряжение равно соответствующему линейному напряжению: Uф = Uл. Между линейными и фазными токами приемника существует соотношение Iл=√3Iф. 
Если не учитывать сопротивлений проводов сети, то напряжения приемника следует считать равными линейным напряжениям источника. На основании схемы и последнего выражения можно сделать вывод о том, что соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника или однофазные приемники рассчитаны на напряжение, равное номинальному линейному напряжению сети. Фазные токи Iab, Ibc и Ica в общем случае не равны линейным токам Ia, Ib и Ic. Применяя первый закон Кирхгофа к узловым точкам a, b, c, можно получить следующие соотношения между линейными и фазными точками:
Используя указанные соотношения и имея векторы фазных токов, нетрудно построить векторы линейных токов. Схема включения треугольником применяется для любых (симметричных и несимметричных) приемников. Мощность трехфазного тока
Под активной мощностью трехфазной системы понимают сумму активных мощностей фаз и активной мощности, выделяемой в сопротивлении, включенном в нулевой провод: Реактивная мощность - сумма реактивных мощностей фаз и реактивной мощности сопротивления, включенного в нулевой провод: Полная мощность: Если нагрузка симметричная, то Здесь под j понимается угол между напряжением UФ и током IФ фазы нагрузки.
При симметричной нагрузке фаз
При симметричной нагрузке независимо от способа ее соединения в "звезду" или в "треугольник"
Поэтому вместо формул (7.11) используют следующие:
опуская индексы для линейных токов и напряжения, S = √3 U I; P = √3 U I cosφ.
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 417. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
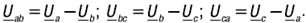
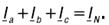
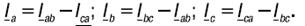
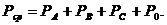
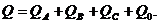
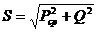
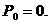
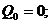
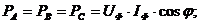
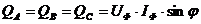 .
. 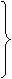
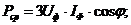
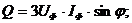
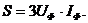
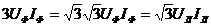 .
.