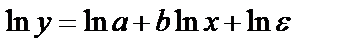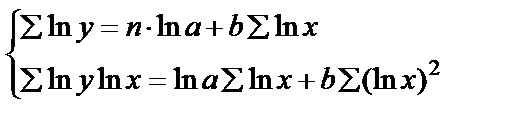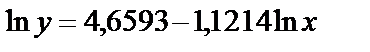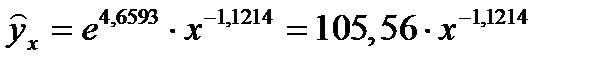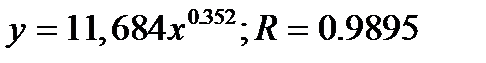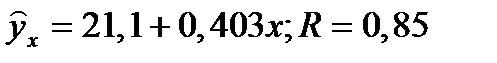Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нелинейные модели регрессии и их линеаризация.I класс: регрессии, нелинейные относительно включённых параметров, но линейные по оцениваемым параметрам. 1) 2) равносторонняя гипербола II класс: регрессии, нелинейные по оцениваемым параметрам. 1) степенная 2) показательная 3) экспоненциальная Нелинейная регрессия по включённым переменным определяется как в ЛР методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так в параболе второй степени Для уравнения третьего порядка получим трехфакторную модель ЛР.
Для полинома к-го порядка Следовательно, полином любого порядка сводится к линейной регрессии с её методами оценивания параметров и проверки гипотез. Как показывает опыт, чаще используется парабола второй степени, редко – полином третьего порядка. Ограничения в использовании полиномов более высокой степени связаны с требованием однородности исследуемой совокупности, чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно, менее однородна совокупность по результативному признаку. Парабола второй степени целесообразна, если для определенного интервала значений фактора меняется характер связи рассмотренных признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем нулю первую производную  Исходные данные не обнаруживают изменения направленности связи и параметры параболы второго порядка становятся трудно интерпретированными, а форма связи часто заменяется другими, нелинейными моделями. МНК для параболы: Решение методом Крамера: где
При b > 0 и c < 0 кривая симметрична относительно высшей точки, то есть мочки перелома кривой. В экономике, зависимость зарплаты работников физического труда от возраста – с увеличением возраста повышается зарплата ввиду повышения опыта и квалификации работника. Однако с определённого возраста ввиду старения организма и снижения производительности труда может приводить к снижению заработной платы. Равносторонняя гипербола для уравнения имеет вид Английский экономист Филипс А. В., анализируя данные более чем за 100-летний период, в конце 50-х годов ХХ века установил обратную зависимость % прироста зарплаты от уровня безработицы.
МНК: При b ≠ 0 имеем обратную зависимость, которая при При c < 0 имеем медленно повышающуюся функцию с верхней асимптотой при Например, взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов) – называются кривыми Энгеля (нем. ст. 1857). Э. Энгель сформулировал закономерность – с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. Однако, это увеличение не у – доля расхода на непродовольственные товары; х – доходы (или общая сумма расходов как индикатор дохода) Равносторонняя гипербола не единственная возможная функция для описания кривой Энгеля, можно использовать полулогарифмическую кривую МНК: Ещё возможно к I классу отнести МНК: Уравнение с квадратными корнями используется в исследованиях урожайности, трудоёмкости сельскохозяйственного производства. Если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных. Класс II нелинейных уравнений по оцениваемым параметрам делится на 2: внутренние линейные и внутренние нелинейные модели. Если нелинейная модель внутренне линейна, то она с помощью специальных преобразований приводится к линейному виду. Если же модель внутренне нелинейна, то она не может быть сведена к линейной функции. При изучении эластичности спроса от цен используется степенная функция Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры а и b неаддитивны. Однако, её можно считать внутренне линейной, ибо логарифмирование данного уравнения по е приводит к линейному виду: Если же Внутренне нелинейны будут модели: Они не могут быть преобразованы в линейные.
Среди нелинейных функций, которые могут быть приведены к линейному виду, степенная функция Это значит, что b показывает, насколько % изменится в среднем результат, если фактор изменится на 1%. Рассмотрим пример Зависимость спроса от цен, с увеличением цен на 1% спрос снижается на 1,12%.
Для степенной функции Коэффициент эластичности можно определить и для других форм связи, то только для степеней функции он представляет собой постоянную величину = b. Для В силу того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то рассчитываем средний показатель эластичности: Для оценки к уравнению b – определяется из системы, а «а» - косвенным путем, после потенцирования величины ln a. Например, Поскольку а – экономически не интерпретируется, то нередко зависимость остаётся в виде логарифмически линейной. В виде степенной функции изучаем не только спрос, но и предложение. Обычно эластичность спроса: b<0, а эластичность предложения: b>0. Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчёт экономического смысла не имеет. Например, тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в %. Вряд ли кто будет определять на сколько % может измениться зарплата с ростом стажа работы на 1%. Или на сколько % изменится урожайность пшеницы, если качество почвы измеряемое в баллах, изменится на 1%. Изучая соотношение ставок межбанковского кредита (у) в % и срока его предоставления в днях (х), получено УР. Э=0,352% лишён смысла ибо срок предоставления не изменяется в %. При использовании для этой же задачи линейной зависимости b=0,403 в % показывает изменение ставок кредита с увеличением срока их предоставления на 1 день. Практическое применение экспоненты возможно, если результативный признак не имеет отрицательных значений. Поэтому, если исследуется, например, финансовый результат деятельности предприятий, среди которых наряду с прибыльными есть и убыточные, то данная функция не может быть использована.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 546. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
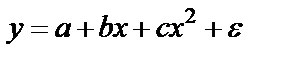 или
или 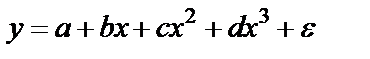 полиномы различных степеней;
полиномы различных степеней;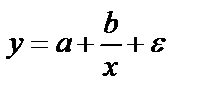 ;
; 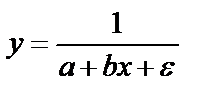 ;
; 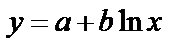 .
.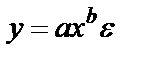
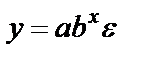
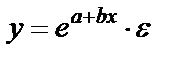
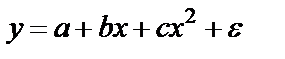 ,заменим
,заменим 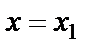 ,
, 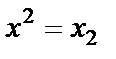 получим двухфакторное уравнение линейной регрессии
получим двухфакторное уравнение линейной регрессии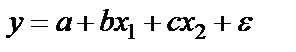
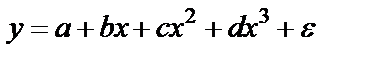
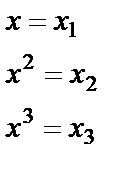
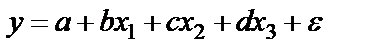 .
.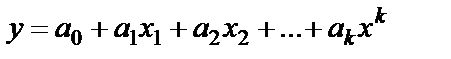 , получим линейную модель множественной регрессии с k объясняющими переменными
, получим линейную модель множественной регрессии с k объясняющими переменными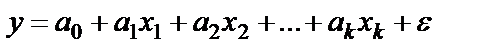 .
.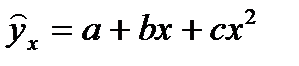 ,
, 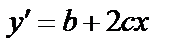 ,
, 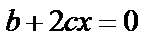 ,
, 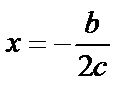 .
.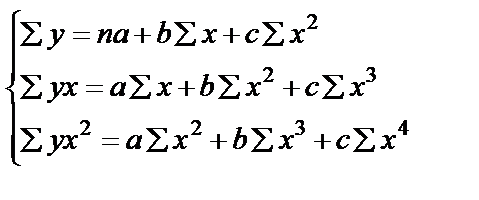
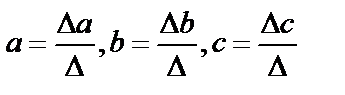 ,
, - главный определитель системы,
- главный определитель системы,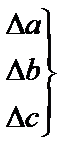 частные определители.
частные определители.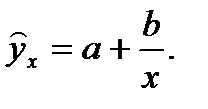 Используется для характеристики связи удельных расходов сырья, материалов, топлива с объёмом выпускаемой продукции, времени обращения товаров от величины товарооборота, то есть на микро- и макроуровнях. Классическим примером её является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы x и % прироста зарплаты у:
Используется для характеристики связи удельных расходов сырья, материалов, топлива с объёмом выпускаемой продукции, времени обращения товаров от величины товарооборота, то есть на микро- и макроуровнях. Классическим примером её является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы x и % прироста зарплаты у: 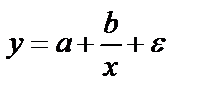 .
.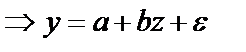 .
.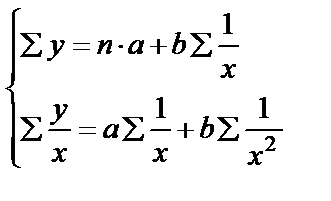
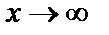 характеризуется нижней асимптотой, то есть минимальным предельным значением у, оценкой которого служит параметр а. Для уравнения Филипса
характеризуется нижней асимптотой, то есть минимальным предельным значением у, оценкой которого служит параметр а. Для уравнения Филипса 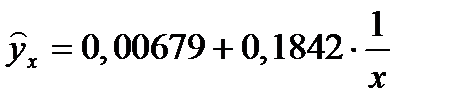 величина параметра а, равная 0,00679, означает, что с ростом уровня безработицы темп прироста зарплаты стремится к 0. Соответственно, можно определить тот уровень безработицы, при котором зарплата оказывается стабильной и темп прироста её равен 0.
величина параметра а, равная 0,00679, означает, что с ростом уровня безработицы темп прироста зарплаты стремится к 0. Соответственно, можно определить тот уровень безработицы, при котором зарплата оказывается стабильной и темп прироста её равен 0.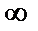 .
.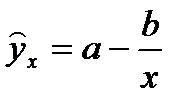
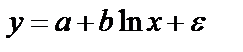 . Заменив
. Заменив 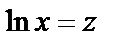 , получим
, получим 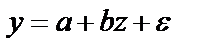 .
.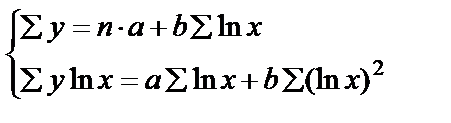
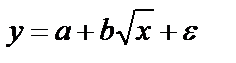 .
.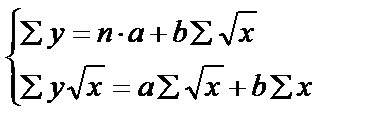
 , где у – спрашиваемое количество, х – цена.
, где у – спрашиваемое количество, х – цена.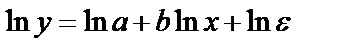 оценка по МНК.
оценка по МНК.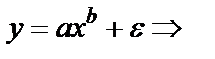 внутренне нелинейна.
внутренне нелинейна.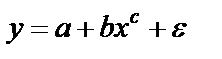 или
или 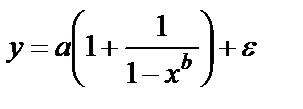
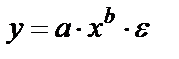 , связано это с тем, что параметр b имеет чёткое экономическое истолкование, то есть он является коэффициентом эластичности.
, связано это с тем, что параметр b имеет чёткое экономическое истолкование, то есть он является коэффициентом эластичности.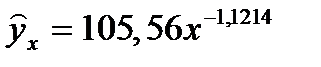
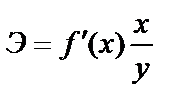
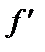 - первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.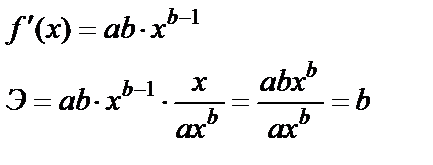 .
.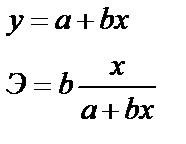 .
.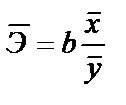 .
.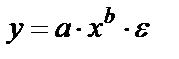 применяется МНК
применяется МНК