
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Законы сложения, умножения и вычитания. ⇐ ПредыдущаяСтр 3 из 3 Операции сложения, умножения и вычитания множеств имеют много общих свойств с операциями сложения, умножения и вычитания чисел. В этом параграфе приведем важнейшие из них, а также докажем несколько теорем, указывающих на различие между алгеброй множеств и арифметикой. Законы коммутативности: а) б) Эти законы непосредственно следуют из законов коммутативности для дизъюнкции и конъюнкции. Законы ассоциативности: а) б) Доказательство основано на законах ассоциативности для дизъюнкции и конъюнкции. Отсюда следует, что при сложении или умножении конечного числа множеств можно опускать скобки, указывающие порядок действий. Например: Законы дистрибутивности: а) б) Доказательство основано на законах дистрибутивности для дизъюнкции и конъюнкции. Например: Законы идемпотентности: а) б) Доказательства получаются непосредственно из законов идемпотентности Докажем несколько законов для операции вычитания.
сравнить: В самом деле, из формул (1) и (2) §2 следует:
Откуда по закону дистрибутивности дизъюнкции относительно конъюнкции имеем:
Поскольку
что и доказывает формулу (5). Из этой формулы следует, что вычитание множеств не является операцией, обратной сложению, как в обычной алгебре чисел. Если, например, А — множество четных чисел, а В — множество чисел, делящихся на 3, то множество Но если  Далее,
В самом деле:
Закон дистрибутивности умножения относительно вычитания имеет вид:
Он получается из эквивалентности
Из равенства (7) следует, что
Законы де Моргана в алгебре множеств имеют вид: а)
б)
Доказательство основано на законах де Моргана алгебры высказываний.
|
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 390. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1)
 (2)
(2)
 .
. (3)
(3)

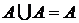 (4)
(4) .
. ,
,  .
. (5)
(5)
 .
. .
. , сомножитель И можно в произведении опустить. Таким образом получим:
, сомножитель И можно в произведении опустить. Таким образом получим: ,
,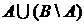 отличается от В, потому что оно содержит все четные числа.
отличается от В, потому что оно содержит все четные числа. , то (согласно (5) и (5) §3)
, то (согласно (5) и (5) §3)  , как в арифметике.
, как в арифметике. (6).
(6). ⇋
⇋ 

 (7).
(7). .
. .
.
 (8)
(8)

 Приведем без доказательств следующие равенства:
Приведем без доказательств следующие равенства: