
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Если множество А и В составлены из одних и тех же элементов, то они равны.Если II. A Аксиома суммы. Для произвольных множеств A и B существует множество, элементами которого являются множества A и все элементы множества B и которое никаких других элементов не содержит. III. B Аксиома разности. Для произвольных множеств A и B существует множество, элементами которого являются те и только те множества A, которые не являются элементами множества B. IV. C Аксиома существования. Существует по крайней мере одно множество. Из аксиом J и A следует, что для произвольных множеств А и В множество, удовлетворяющее условиям аксиомы А, единственно. В самом деле, если бы были два таких множества С1 и С2, то они оба содержали ли бы одни и те же элементы (все элементы множества А, и все элементы, принадлежащие В), и поэтому, согласно аксиоме J, было бы С1 = С2. О п р е д е л е н и е 1. Это единственное множество, удовлетворяющее условиям аксиомы А, назовем суммой (или объединением) множеств А и В и будем обозначать символом
О п р е д е л е н и е 2. Подобным образом из аксиом J и B заключаем, что для произвольных множеств А и В существует в точности одно множество, содержащее элементы множества А, не принадлежащее множеству В. Это множество называется разностью множеств А и В и обозначается символом А–В. (А\В)
Из закона де Моргана и закона двойного отрицания следует также, что
то есть x не принадлежит разности С помощью операций  О п р е д е л е н и е 3. Произведение (пересечение)
Из определения разности имеем для произвольного х
откуда по (3) и первому закону дистрибутивности
О п р е д е л е н и е 4. Симметрическую разность
Включение. Пустое множество. О п р е д е л е н и е 5. Множество A называется подмножеством множества В, если каждый элемент подмножества А принадлежит множеству В. В этом случае мы пишем Свойства включения. Из определения
Очевидно, что из
Далее
Отношение включения транзитивно:
Сумма двух множеств содержит каждое слагаемое:
Произведение двух множеств содержится в каждом сомножителе:
В самом деле, из закона
и, согласно (1) из §2 , Второе утверждение в (3) доказывается аналогично. Для доказательства (4) нужно использовать закон
Из (2) §2 следует включение
Отношение включения можно определить при помощи отношения равенства и одной из операций
В самом деле, если
что доказывает, что С другой стороны, Обратно, если Из аксиомы разности (аксиома B §2) следует, что, если существует хотя бы одно множество А, то существует множество А – А, не содержащего ни одного элемента. Такое множество единственно. В самом деле, если бы было два таких множества
была бы истинна, так как оба ее члена ложны. Тогда Единственное множество, не содержащее ни одного элемента, называется пустым множеством ( Для каждого x
Поскольку импликация с ложной посылкой истинна, для каждого x верна импликация.
Таким образом, пустое множество является подмножеством любого множества. Из формулы (1) §2 следует, что
так как
Равенство Равенство Роль пустого множества в теории множеств аналогична роли числа нуль в алгебре. Без множества 0 операции умножения и вычитания множеств не всегда были бы выполнимы, что в последствии привело бы к значительным трудностям при вычислениях.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 245. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 для каждого x, то А=В.
для каждого x, то А=В. . Для производных х и производных множеств А и В верны эквиваленты.
. Для производных х и производных множеств А и В верны эквиваленты. ⇋
⇋ 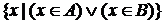
 (1)
(1)
 ⇋
⇋ 
 (2)
(2)
 (3)
(3) , если х не принадлежит А или принадлежит В.
, если х не принадлежит А или принадлежит В. и \ можно определить еще две операции на множествах.
и \ можно определить еще две операции на множествах. множеств А и В определяем по формуле
множеств А и В определяем по формуле ⇋
⇋ 

 ,
,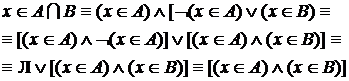
 двух множеств А и В определяем как
двух множеств А и В определяем как

 или
или  и говорим, что множество А содержится в В. Отношение
и говорим, что множество А содержится в В. Отношение  называется отношением включения.
называется отношением включения. следует:
следует: (1)
(1)
 следует
следует  , то А – собственное подмножество множества В.
, то А – собственное подмножество множества В.

 , потому что по определению
, потому что по определению , откуда следует, что
, откуда следует, что  и А=В в силу аксиомы J.
и А=В в силу аксиомы J. (2)
(2) (3)
(3) (4)
(4) , следует, что для каждого x
, следует, что для каждого x
 , а, следовательно, по (1)
, а, следовательно, по (1)  .
. .
.

 .
. (5)
(5) для каждого x и тогда в силу закона
для каждого x и тогда в силу закона 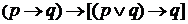 имеем:
имеем: , откуда
, откуда ,
, .
. , значит
, значит  .
. формулы (5) доказывается аналогично.
формулы (5) доказывается аналогично. , то для каждого x эквивалентность
, то для каждого x эквивалентность
 в силу аксиомы J.
в силу аксиомы J. ).
). или
или 


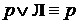 . Отсюда заключаем, что
. Отсюда заключаем, что  , а из закона
, а из закона 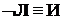
 .
. означает, что множества А и В не имеют общих элементов, то есть не пересекаются.
означает, что множества А и В не имеют общих элементов, то есть не пересекаются. означает, что
означает, что