
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Множества и операции на множествах.Стр 1 из 3Следующая ⇒ О г л а в л е н и е ВВЕДЕНИЕ……………………………………………………………………... 3 ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ…………………………………………. 13 § 1.Множества и операции на множествах…………………………………… 13 §2. Включение. Пустое множество…………………………………………… 16 §3. Законы сложения, умножения и вычитания……………………………… 19 §4. Свойства симметрической разности……………………………………… 23 §5. Множество 1. Дополнение………………………………………………… 28 §6. Конституенты………………………………………………………………. 30 §7. Применение алгебры множеств к отношениям………………………….. 40 §8. Булевы алгебры…………………………………………………………….. 47 § 9. Решетки……………………………………………………………………. 57 Глава II. Аксиомы теории множеств. Отношения. Функции……………………………………………………………………… 61 § 1. Высказывательные функции. Кванторы…………………………………. 61 § 2. Аксиомы теории множеств……………………………………………….. 69 § 3. Простейшие следствия из аксиом………………………………………… 74 § 4. Декартовы произведения. Отношения…………………………………… 78 § 5. Отношение эквивалентности……………………………………………… 82 § 6. Функции……………………………………………………………………. 86 § 7. Образы и прообразы………………………………………………………. 91 § 8. Функции, согласованные с данным отношением эквивалентности. Булевы факторкольца………………………………………………………….. 95 § 9. Отношение порядка……………………………………………………….. 98 § 10. Реляционные системы, их изоморфизмы и типы…………………….. 103 ГЛАВА III. НАТУРАЛЬНЫЕ ЧИСЛА. КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ МНОЖЕСТВА………………………………………………………………... 107  §1. Натуральные числа……………………………………………………….. 107 §2. Определения по индукции……………………………………………….. 111 §3. Отображение множества N §4. Конечные и бесконечные множества…………………………………… 123 §5. Теорема Д. Кёнига………………………………………………………... 129 §6. Графы. Теорема Рамсея………………………………………………….. 132 ГЛАВА IV. БЕСКОНЕЧНЫЕ СУММЫ, ПРОИЗВЕДЕНИЯ И ДЕКАРТОВЫ ПРОИЗВЕДЕНИЯ……………………………………………………………. 136 §1. Бесконечные суммы и произведения……………………………………. 136 §2. Операции на бесконечных последовательностях множеств…………... 146 §3. Семейства множеств, замкнутые относительно данной операции……. 151 §4. §5. Обобщённые декартовы произведения…………………………………. 157 §6. Декартовы произведения топологических пространств………………. 161 § 7. Теорема Тихонова……………………………………………………….. 167 §8. Приведенные Декартовы произведения………………………………… 171 § 9. Обратные системы и их пределы……………………………………….. 176 § 10. Бесконечные операции в решетках и булевых кольцах……………… 180 § 11. Расширение упорядоченного множества до полной решетки………. 187 §12. Теория представления дистрибутивных решеток…………………….. 194 ГЛАВА V. ТЕОРИЯ КАРДИНАЛЬНЫХ ЧИСЕЛ………………………….. 200 §1. Равномощность множеств. Кардинальные числа………………………. 201 § 2. Счетные множества……………………………………………………… 208 § 3. Шкала кардинальных чисел……………………………………………... 213 § 4. Арифметика кардинальных чисел……………………………………… 217 § 5. Неравенства между кардинальными числами. Теорема Кантора-Бернштейна и ее обознчения………………………………………………… 221 § 6. Свойства чисел ℵ0 и C…………………………………………………... 229 § 7. Обобщенные суммы кардинальных чисел……………………………... 234 § 8. Обобщенные произведения кардинальных чисел…………………….. 240 ГЛАВА VI . ЛИНЕЙНО УПОРЯДОЧЕННЫЕ МНОЖЕСТВА…………… 245 § 1. Введение…………………………………………………………………. 245 § 2. Плотные, разреженные и непрерывные множества…………………… 250 § 3. Типы ω, η, λ ……………………………………………………………… 256 § 4. Арифметика порядковых типов………………………………………… 262 § 5. Лексикографический порядок…………………………………………... 264 Литература…………………………………………………………………….. 267
Условные обозначения
Многие рассуждения в теории множеств можно сделать очень наглядными, если пользоваться логическими символами и логическими законами, сформулированными в этой символике. В этом параграфе приведем основные сведения из логики, на которые в дальнейшем будем ссылаться. Алгебра высказываний — составная часть алгебры логики и представляет собой один из основных разделов математической логики, в котором методы алгебры применяются для изучения операций под высказываниями, т. е. над предложениями, в отношении каждого из которых имеет смысл утверждать только то, что его содержание истинно либо ложно [10]. Пример. «На улице дождь» — истинное. «Мел, который я Вам дал — черный» — ложное. Очевидно, утверждать истинное или ложное предложение (высказывание) можно только в отношении повествовательных предложений. Произвольные высказывания будут обозначать прописными латинскими буквами: p, q, r,…. Алгебра высказываний включает: 1. переменные — высказывания (p, q, r); 2. постоянные — операции (связи) над высказываниями. Из двух произвольных высказываний p, q можно получить новое высказывание, связывая высказывания p и q одним из союзов (связок): 1. не; 2. и; 3. или; 4. если …, то …; 5. тогда и только тогда, когда …. Процесс образования сложных высказываний из простых в алгебре высказываний формируется следующим образом: сложное высказывание (предложение, рассуждение) записывается в виде логических формул, где: а) переменными (p, q, r,…) обозначаются простые (атомарные) предложения, в отношении которых можно четко сказать истинны они или ложны, т. е. переменные p, q, r… имеют только 2 значения (И — истинно, Л — ложно); б) постоянными ( в) скобки (( ), [ ], { }) — для однозначности чтения логических формул. Атомарные высказывания, образующие сложные высказывания, называются членами. Укажем исходные (элементарные) высказывания. 1. Высказывание p и q записываем в виде Таблица значений сложных высказываний:
2. Высказывание p или q, которое записываем в виде Например. 3. Высказывание если p, то q называется импликацией с посылкой (условием) p и заключением (следствием) q. Обозначение импликации (если p, то q): Импликация ложна, если ее заключение ложно, в то время как посылка истинна. Во всех остальных случаях импликация истинна. В повседневном языке смысл слов «если …, то …» не вполне совпадает с описанным выше их значением. Однако в математике данное определение оказывается удобным. 4. Высказывание p тогда и только тогда, когда q называется эквивалентностью с членами p и q. В обозначениях эквивалентность:
Высказывание 5. Высказывание не p называется отрицанием p и записывается в виде Так как истинность или ложность высказываний, построенных с помощью связок ( Если все эти значения раны И, то исследуемое выражение есть логический закон, если хотя бы одна подстановка дает Л, то это не логический закон. Пример: 1.
2. Приведем несколько наиболее важных логических законов: 1. Закон коммутативности (перестановки): а) для дизъюнкции: б) для конъюнкции: 2. Закон ассоциативности (объединения): а) для дизъюнкции: б) для конъюнкции: 3. Закон дистрибутивности (распределения): а) первый закон (дистрибутивности конъюнкции относительно дизъюнкции): Например (Д. Гилберт) б) второй закон (дистрибутивности дизъюнкции относительно конъюнкции): 4. Закон идемпотентности (лат. Idempotens – сохраняющий ту же степень) – закон математики, по которому из логики исключаются коэффициенты и показатели степеней. (p
5. Закон поглощения: В этих законах усматривается отдаленная аналогия между алгеброй высказываний и обычной математикой. Главное отличие заключается во 2-м законе дистрибутивности, законах идемпотентности и поглощения. Из законов идемпотентности следует, что в алгебре высказываний не нужны ни показатели степеней, ни коэффициенты. 6. Закон силлогизма (греч. Syllogismos - сосчитывание) – умозаключение, в котором из двух категорических суждений, связанных общим средним термином, получится третье суждение, называемое выводом; при этом средний термин в заключение не входит. Студент Иванов – гражданин СССР Все граждане СССР имеют право на труд. Студент Иванов имеет право на труд.
7. Закон исключенного третьего – один из основных законов формальной логики, согласно которому из двух противоречащих высказываний в одно и то же время и в одном и том же отношении одно непременно истинно.
8. Закон противоречия: «Доска черная и доска белая» 9. Закон двойного отрицания:
10. Законы де Моргана: а) б) Например: 11. Закон контрапозиции(лат. Contraposition – противопоставление).
Например: «Если через проволоку провести ток, то проволока нагреется». Контрапозитивным высказыванием будет: «Если проволока не нагрелась, то через проволоку не пропущен ток.» 12. 13. 14. 15. Всюду, где мы будем писать выражения, употребляя логические символы, мы будем подразумевать, что они истинны. Замечания, помещенные перед высказыванием или после него, содержат доказательства его истинности.
ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ.
Множества и операции на множествах. Основное понятие теории множеств – «множество». Это понятие по мере развития теории претерпело значительные изменения. В начальный период развития теории множеств, во время так называемой « »теории множеств, пользовались интуитивным понятием множества, т.е. слово «множество» имело такое же и столь же неопределенное значение, как и в обычном языке. В частности, такую позицию занимал создатель теории множеств Кантор. Но такое положение долго не продержалось. Интуитивное понимание множества оказалось в некоторых случаях порочным. В гл. II §2. мы скажем о так называемых антимониях теории множеств, т.е. об очевидных противоречиях, появившихся на определенной стадии развития это науки. Причиной их была возникающая в сложных случаях неясность интуиции, связанной с понятием множества. В полемике, развернувшейся вокруг антимоний, было выяснено, что разные математики вкладывают в понятие множества существенно различный смысл. Поэтому построение теории множеств исключительно на интуитивной основе оказалось невозможным. В этом курсе лекций теория множеств будет изложена в виде аксиоматической системы. Подобно тому как в геометрии, не отвечая на вопросы, что такое точка, прямая, плоскость и другие «первичные термины», мы из определенной системы аксиом выводим все теоремы, не обращаясь к смысловому значению первичных терминов, так и в теории множеств мы будем исходить из аксиом и дедуктивным путем получать теоремы. Хотя эти аксиомы основаны на интуитивном понимании множеств, но благодаря аксиоматическому методу интуитивное содержание этого понятия не будет привлекаться ни при доказательствах теорем, ни в определениях. Первичные понятия теории множеств – множество и отношение быть элементом. Вместо х есть множество будем писать Z(x), вместо х есть элемент множества y – Отрицание выражения Для упрощения символики будем употреблять прописные латинские буквы для обозначения множеств, т.е. если в выражении встретится, например, буква А, то предполагается, что А – множество. Кроме этих двух первичных понятий, мы в дальнейшем вносим еще одно первичное понятие xTRy (x есть регуляционный тип y), которое будет разъяснено в главе II. Cначала выведем четыре аксиомы: (Интуитивный принцип объемности, Р. Столл, стр. 13) I. J Аксиома объемности (экстенсивности). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 263. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 N на N и связанные с ним отображения... 117
N на N и связанные с ним отображения... 117 - аддитивные и
- аддитивные и 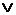
 ,
, 
 ,
, 
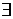




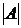


 (
(  )
)







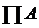

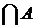

 на
на 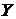


 ,
,  ,
,  ,
,  , ~
, ~

 ,
,  ,
, 







 ) обозначены соединительные союзы (не, и, или, если …, то, тогда и только тогда, когда…), с помощью которых образованы новые высказывания;
) обозначены соединительные союзы (не, и, или, если …, то, тогда и только тогда, когда…), с помощью которых образованы новые высказывания; Оно называется конъюнкцией, или логическим произведением высказываний p и q, называемых сомножителями конъюнкции. (Например:
Оно называется конъюнкцией, или логическим произведением высказываний p и q, называемых сомножителями конъюнкции. (Например:  ).
).
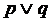
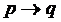


 , называется дизъюнкцией, или логической суммой высказываний p и q (слагаемых дизъюнкции). Дизъюнкция истинна, если хотя бы одно из ее слагаемых истинно, и ложна только тогда, когда оба слагаемых ложны.
, называется дизъюнкцией, или логической суммой высказываний p и q (слагаемых дизъюнкции). Дизъюнкция истинна, если хотя бы одно из ее слагаемых истинно, и ложна только тогда, когда оба слагаемых ложны. .
. .
. .
. . Отрицание p имеет логическое значение, противоположное значению p.
. Отрицание p имеет логическое значение, противоположное значению p.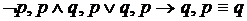 ), определяем логические значения полученных таким образом выражений.
), определяем логические значения полученных таким образом выражений. — не закон.
— не закон.

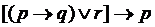
 — логический закон.
— логический закон. ;
;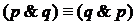 .
.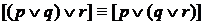 ;
; .
.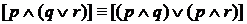 (
(  ).
).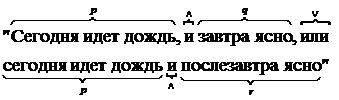
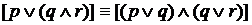 — нет аналога в обычной алгебре:
— нет аналога в обычной алгебре:  .
. p)
p)  p [в алгебре:
p [в алгебре:  ]
] [в алгебре:
[в алгебре:  ]
]



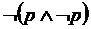
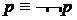








 .
. или
или  или х non
или х non  y.
y.