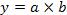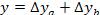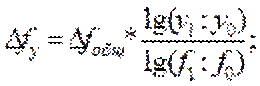Математические способы, используемые в детерминированном анализе: интегральный и логарифмический.

Интегральный способ применяется для измерения влияния фак­торов на изменение результативного показателя в мультипликатив­ных, кратных и смешанных кратно-аддитивных моделях.

Использование данного способа позволяет получать более точ­ные результаты расчета влияния факторов по сравнению со способа­ми элиминирования, так как дополнительный прирост результативно­го показателя от взаимодействия факторов присоединяется не к по­следнему фактору, а делится поровну между ними.

Алгоритм расчета влияния факторов на изменение результатив­ного показателя в двухфакторной мультипликативной модели инте­гральным способом включает следующие этапы.

1 этап. Построение факторной модели результативного пока­зателя:

где у - результативный показатель;

а, b - факторные показатели, имеющие с результативным показа­телем мультипликативную зависимость.

2 этап. Определение абсолютного изменения результативного показателя:

базисное значение результативного показателя:у₀ = а₀ ∙ b₀;

фактическое значение результативного показателя: у₁ = а₁ ∙ b₁

∆у = у₁ - у₀

3 этап. Расчет влияния факторов на абсолютное изменение результативного показателя:

4 этап. Проведение балансовой увязки полученных результатов:

∆

∆у = ∆у

5 этап. Формулирование выводов по результатам проведенного анализа.

Использование интегрального способа не требует знания всего процесса интегрирования. Достаточно в готовые рабо­чие формулы подставить необходимые числовые данные и произве­сти расчеты с помощью калькулятора или ПЭВМ в Ехсе1.

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения). Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = хуz. Влияние данных факторов определяется следующим образом:

Из формул следует, что общий прирост результативного показа­теля распределяется по факторам пропорционально отношениям ло­гарифмов факторных индексов к логарифму результативного пока­зателя. И не имеет значения, какой логарифм используется — нату­ральный или десятичный.