
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Канонические уравнения метода силСтатически определимая основная система отличается от заданной статически неопределимой тем, что по направлениям отброшенных лишних связей мы будем иметь перемещения, которых быть не должно.Смыслканонических уравнений метода сил (10.4) состоит в том, что каждая строка является перемещением по направлению отброшенной связи, которое приравнивается нулю. Так для рамы на рис. 10.4 имеем систему из трех канонических уравнений (10.4)
Рассмотрим физический смысл первой строки (10.4) для случая основной системы, представленной, например, на рис 10.4, б. d11 – это перемещение в основной системе по направлению первой неизвестной X1 от нее самой, но принятой равной единице (его называют единичным перемещением), то есть при Вторая неизвестная X2 также создает свой вклад в перемещение правой опоры основной системы по направлению X1. d12 – это единичное перемещение по направлению X1 от Третья неизвестная – реактивный момент X3 также создает перемещение правой опоры в основной системе по направлению X1. d13 – это единичное перемещение по направлению X1 от Δ1F– это перемещение по направлению X1 от нагрузок, действующих на основную систему. Естественно, что в статически неопределимой системе суммарное перемещение по направлению X1 равно нулю. Это и есть смысл первого канонического уравнения.  Вторая строка свидетельствует о том, что суммарное перемещение по направлению X2 в основной системе равно нулю, а третья – что перемещение по направлению X3 равно нулю. Число канонических уравнений равно числу неизвестных метода сил. Для определения перемещений, входящих в систему уравнений используется метод Мора, рассмотренный ранее. Так, для определения единичных перемещений dij следует применить формулу:
где: Из (10.5) следует, что
Для определения перемещения точек от приложенных к системе внешних нагрузок воспользуемся формулой:
где
|
|||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 583. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
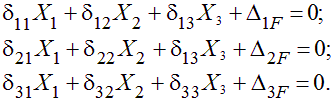
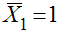 . Естественно, что, когда мы умножим d11 на истинную, неизвестную пока, величину X1, мы получим перемещение по направлению X1 от нее самой в основной системе.
. Естественно, что, когда мы умножим d11 на истинную, неизвестную пока, величину X1, мы получим перемещение по направлению X1 от нее самой в основной системе.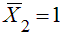 . При умножении его на истинную величину X2 получим перемещение по направлению X1 от X2.
. При умножении его на истинную величину X2 получим перемещение по направлению X1 от X2.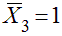 . Если умножить d13 на истинную величину X3, то получим перемещение по направлению X1 от X3.
. Если умножить d13 на истинную величину X3, то получим перемещение по направлению X1 от X3.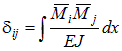 .
.
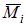 – изгибающий момент от усилия
– изгибающий момент от усилия 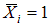 ;
; 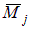 – изгибающий момент от усилия
– изгибающий момент от усилия 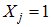 .
.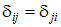 .
.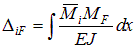 .
.
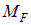 – изгибающий момент от внешних нагрузок (грузовая эпюра).
– изгибающий момент от внешних нагрузок (грузовая эпюра).