Степень статической неопределимости

Особенности статически неопределимых конструкций

Статически неопределимыми системами называют геометрически неизменяемые системы, в которых невозможно найти неизвестные опорные реакции и внутренние усилия, используя уравнения статики.

Количество уравнений статики для плоской стержневой системы равно трем, и они позволяют найти три неизвестных, для пространственной – имеем шесть уравнений статики. Если число неизвестных больше, чем уравнений статики, система становится статически неопределимой.

Статически неопределимая система содержит лишние связи, удаление которых переводит систему в статически определимую и геометрически неизменяемую.

Отметим некоторые самые важные особенности статически неопределимых систем.

1. Статически неопределимая система, благодаря наличию лишних связей, оказывается более жесткой по сравнению с той неизменяемой статически определимой системой, из которой она может быть получена. Величины прогибов в статически неопределимых системах, как правило, оказываются меньшими, чем в аналогичных статически определимых системах.

2. Удаление лишних связей не приводит к образованию геометрически изменяемой системы (механизма) вплоть до того момента, когда будут удалены необходимые связи, то есть статически неопределимая система имеет резерв прочности в виде лишних связей. Вот почему необходимо изучать не только напряжения и условия прочности, но, также и кинематический анализ. Если удалить не лишние, а необходимые связи при реконструкции или ремонте сооружения, такое действие может привести к аварии и разрушению конструкции.

3. В статически неопределимой системе распределение усилий зависит от соотношения жесткостей сечений элементов системы.

4. В статически неопределимых системах возникают дополнительные усилия от смещения опор, температурных воздействий и неточностей монтажа, чего не происходит в статически определимых системах.

Степень статической неопределимости

Для плоской стержневой системы может быть определена числовая безразмерная характеристика n, которая называется степенью статической неопределимости. Напомним, что ее можно получить несколькими способами.

Первый способ состоит в вычислении разницы между числом статических неизвестных и числом уравнений статики.

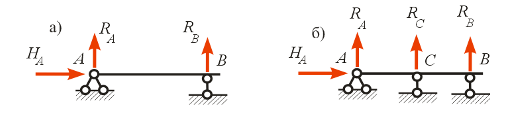
где: n – степень статической неопределимости; p – количество неизвестных; k – число уравнений статики (k = 3 для плоской системы, k = 6 для пространственной стержневой системы).

Для балки на рис. 10.1,а имеем n = 3 – 3 = 0, т.е. эта балка статически определима. Если мы поставим в точке С еще одну шарнирно-подвижную опору (рис. 10.1,б), то количество неизвестных станет равно четырем и мы получим n = 4 – 3 = 1, т.е. такая система станет один раз статически неопределимой.

Рис. 10.1. Статически определимая (а) и статически неопределимая (б) балки

Существует зависимость, связывающая степень статической неопределимости со степенью свободы стержневой системы

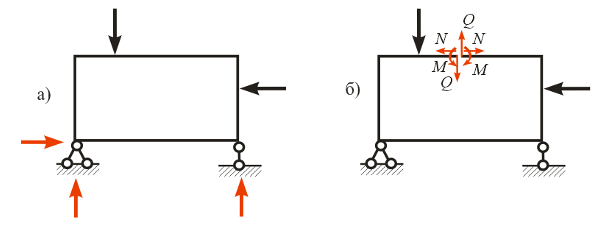
где символом W обозначена степень свободы (см. главу 7).

Второй способ вычисления степени статической неопределимости состоит в определении степени свободы стержневой системы, после чего, взятая с обратным знаком, она даст значение степени статической неопределимости.

Третий способ связан с понятием лишних связей.

Статически определимая балка (рис. 10.1,а) не обладает лишними связями, так как удаление любой из них превратит балку в механизм. Например, если удалить опору В, балка повернется вокруг точки А и упадет на землю. Поэтому степень статической неопределимости для нее n=0.

Статически неопределимая балка, изображенная на рис. 10.1, б обладает одной лишней связью, которую можно удалить. Такой лишней связью будет, например, опора в т. С, так как даже без нее балка будет выполнять свои функции. Поэтому эту балку можно считать один раз статически неопределимой.

Подобные рассуждения приводят к следующему определению.

Степень статической неопределимости n равна числу лишних связей, удаление которых преобразует данную систему в статически определимую и геометрически неизменяемую.

В раме, содержащей замкнутый контур с жесткими узлами (рис. 10.2, а), не удастся построить эпюры внутренних усилий. На первый взгляд кажется, что эта рама статически определима. Действительно, определение трех опорных реакций не представляет большого труда (они находятся из трех уравнений статики). Замкнутый контур является сам по себе трижды статически неопределимой конструкцией, а неизвестными являются не опорные реакции, а внутренние усилия М, Q и N, изображенные на рис. 10.2,б на сквозном разрезе. Такие системы называют внутренне статически неопределимыми. Представленная на рис. 10.2, а рама является трижды статически неопределимой.

Рис. 10.2. К определению n в рамах с замкнутыми контурами

Чтобы обеспечить жесткое соединение смежных частей, отделенных разрезом, можно использовать принцип 2, согласно которому это можно сделать посредством трех связей, не параллельных и не пересекающихся в одной точке. Таким образом, количество лишних связей для замкнутого контура равно трем. Это подтверждает вывод о том, что степень статической неопределимости замкнутого контура равна трем.

Если бы такая рама имела шарнир, врезанный в замкнутый контур (рис. 10.3,а), то изгибающие моменты М в шарнирестали бы равны нулю и в сечении по шарниру были бы только два неизвестных Q и N. Если ввести два шарнира (рис. 10.3,б), то можно понизить степень статической неопределимости на две единицы, а если в замкнутый контур добавить три шарнира, то сам контур станет статически определимым (рис. 10.3,в) и в раме удастся построить эпюры внутренних сил. Это лучше всего сделать путем построения поэтажной схемы.

Рис. 10.3. К определению степени статической неопределимости замкнутого контура.

Отсюда можно заключить, что введение одного простого шарнира в замкнутый контур уменьшает степень статической неопределимости контура и всей стержневой системы на единицу.

Эти рассуждения приводят к весьма простой и универсальной формуле для определения степени статической неопределимости в любой плоской стержневой системе, включающей замкнутые контура, в том числе в каркасах многоэтажных жилых и производственных зданий.

Здесь: К – количество замкнутых контуров, Ш – число простых шарниров (простым называется шарнир, соединяющий два стержня). Более подробно о шарнирах было рассказано в главе, посвященной кинематическому анализу.

Расчет статически неопределимых систем начинается с установления степени статической неопределимости.