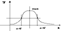Нормальное распределение. Его параметры и график.

Нормальным распределением называется распределениее, имеющее плотность вида: f (x) = ( 1 / σ √ ( 2 π ) ) * e ^ ( ( x – a) ² / 2σ ²)

где a и σ - два параметра, а именно a=M(x), σ=σ (х)=√D(x).

Опр: График нормальной распределения назыв нормальной кривой (кривой Гаусса)

Рассмотрим график:

1) Область определения: D(f(x))=(–∞; +∞) x принадлежит R

2) Область значений: E(f(x))=(0; +∞)

3) y=0 – горизонтальная асимптота

4) f ’ (x) = ( 1 / σ √ ( 2 π ) ) * e ^ ( ( x – a) ² / 2σ ²) * (( – 2 ( x – a ) ) / ( 2 σ ² ))

f ’(x) = 0         x = a – критическая точка, точка максимума

f ( a ) = 1 / σ √ ( 2 π)       ( a ; 1 / σ √ ( 2 π)) – координаты точки максимума

5) Точки перегиба x = a ± σ

6) График функции симметричен относительно прямой x = a

Оценка отклонения теоретического распределения от нормального. «Правило трёх s». Асимметрия и эксцесс.

Очень часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины Х по абсолютной величине меньше заданного положительного числа δ (дельта).

P ( | x – a |< δ ) = ?                 | x - a| < δ                =>   - δ < x-a < δ              =>             

=>    a – δ < x < a + δ          =>           P( |x-a| < δ )=Ф(δ/σ)-Ф(-δ/σ) = 2Ф(δ/σ)

Ф(х) – функция Лапласа.

«Правило трёх s»: Оно означает, что вероятность того, что модуль отклонения случ вел Х превзойдёт утроенное среднее квадратическое отклонение равно 0.0027, т.е. такое возможно лишь в 0.27% случаев, и следовательно, по принципу невозможности маловероятных событий, событие Р( |x-a|>3s) встречается достаточно редко, т.е. практически невозможно.

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики (асимметрию и эксцесс).

Опр: Асимметрией НСВ Х назыв отношение центрального теоретического момента 3-го порядка m₃ к кубу среднего квадратического отклонения s³, т.е. As=m₃/s³

Опр: Эксцессом сл вел Х назыв величина равная E_k = (m₄/s⁴)–3