Функция распределения вероятностей случайной величины. Её свойства.

Случ. величины. Основные понятия. Законы распределения ДСВ.

 Опр: Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Опр: Дискретной случайной величиной (ДСВ) называют величину, которая принимает отдельные изолированные значения с определённой вероятностью.

Опр: Непрерывной называют случайную величину, которая принимает все возможные значения из некоторого промежутка.

Опр: Законом распределения случайных величин называется всякое соответствие м/у возможными значениями случ вел и вер-ми их осуществления.

Закон распределения ДСВ может быть записан в виде таблицы, графика :

Так как события x₁, x₂, … , x_n образуют полную группу, то сумма вероятностей этих событий равна 1, т.е. p₁+p₂+…+p_n=1.

Виды законов распределения дискретной случайной величины:

1.Биномиальный закон: Р = С_n^k ∙ p^k ∙ q^n-k

2.Распределение Пуассона: Р = (λ ^k ∙ e ^{– λ} )/k!, где k = n ∙ p

3.Геометрический закон: Р = q ^{k - 1} ∙ p

4.Гипергеометрический закон: P = (C_n^m ∙ C_{N - n}^{M – m}) / C_N^M

Биномиальное закон и закон Пуассона.

Биномиальный закон: Р = С_n^k ∙ p^k ∙ q^n-k

Биномиальный закон основывается на формуле Бернулли. В нём С_n^k –коэффициент в разложении в бином Ньютона. Если в биномиальном законе n>30 и p<0,01, то применяют закон Пуассона: Р = (λ ^k ∙ e ^{– λ} )/k!, где k = n ∙ p

Геометрический закон.

Пусть производятся независимые испытания в каждом из которых вероятность появления события А одна и та же = р, а не появления q=1-р.

Пусть событие А в k-1 испытаниях не появляется, а в k-ом испытании появилось, тогда по теореме умножения вероятностей независимых событий

=>  Р = q ^{k - 1} ∙ p

Определение числовых характеристик случайных величин. Мат ожидание д.с.в. и его свойства.

Случайная величина полностью описывается законом распределения, но иногда он неизвестен. В этом случае используют числа, которые описывают ДСВ суммарно, их назыв числовыми характеристиками.

К ним относятся: мат ожидание М(X), дисперсия D(X), среднее квадратическое отклонение σ(X), начальный ν_k(X) и центральный μ_k(X) теоретические моменты, мода Mo(X), медиана Me(X), асимметрия As(X) и эксцесс Ek(X).

пусть задан закон распределения:

Опр: Мат ожиданием ДСВ называется сумма произведений возможных значений случайной величины на их вероятности.

 М(х) = ∑(от k=1 до n) x_k ∙ p_k = x₁ ∙ p₁ + x₂ ∙ p₂ +…+ x_k ∙ p_k

С точки зрения вероятности мат ожидание – есть среднее арифметическое возможных значений случайной величины.

Свойства математического ожидания:

1.M(C)=C, С-const.

2.M(CX)=CM(X)

3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(X*Y)=M(X)*M(Y).

4.M(X+Y)=M(X)+M(Y).

5. Пусть производится n независимых испытаний, в каждом из которых событие А появляется с одной и той же вероятностью p, тогда математическое ожидание числа появлений события А равно: M(X)=np.

Дисперсия ДСВ. Её свойства. Среднее квадратическое отклонение д.с.в.

Опр: Отклонением случайной величины Х от её математического ожидания называется соответствующая разность: [X-M(X)]

Опр: Дисперсией (рассеянием) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания. D(X)=M[X-M(X)]²

Для вычислений удобна формула: D(X)=M(X²)-[M(X)]²

С точки зрения вероятности дисперсия представляет собой характеристику рассеяния случайной величины Х вокруг ее математического ожидания.

Свойтсва:

1.D(C)=0

2.D(Х) > 0

3.Х,У- независ, D(X ± Y)=D(X) + D(Y)

4.Пусть в n независимых испытаниях, событие А появляется с 1й и той же вероятностью p и не появиться с вер-тью q=1-р, тогда дисперсия числа появлений события А: D(X)=n∙p∙q

Еще одной характеристикой рассеяния возможных значений случайной величины вокруг ее мат ожидания явл-ся среднее квадратическое отклонение.

Опр: Средним квадратическим отклонением s(х) наз корень из дисперсии.

Среднее квадратическое отклонение применяется тогда, когда размерность результата должна совпадать с размерностью случайной величины.

Начальные и центральные теоретические моменты ДСВ. Мода. Медиана. Асимметрия. Эксцесс.

Опр: Начальным теоретическим моментом k-ого порядка случайной величины X называется математическое ожидание k-ой степени случ вел-ны. n_k = M ( X ^k )

Частный случай: n₁=M(X); n₂=M(X²); Следовательно, D=n₂ - (n₁)²

Опр: Центральным теоретическим моментом k-ого порядка сл вел Х называется мат ожидание от k-й степени отклонения сл вел. m_k = M ( X – M ( X ) ) ^k

Частный случай: m₁= M ( X – M ( X ) )=0 (по основному свойству отклонения);

m₂= М (( X – M ( X ) ) ² )=D(X).

m₂=n₂ – (n₁)²  – связь м/у начальным и центральным моментами.

m₃=n₃–3n₂n₁+2(n₁)³;            m₄=n₄–4n₃n₁+6n₂(n₁)²–3(n₁)⁴;

Опр: Модой случайной величины Х называется наиболее вероятное ее значение Мо(Х). Данное определение справедливо только для ДСВ.

Опр: Асимметрией сл вел Х наз отношение центрального теоретического момента 3-го порядка к кубу среднего квадратического отклонения. As=m₃ / s³

Опр: Эксцессом случайной вел-ны Х называется величина равная E_k=(m₄ / s⁴)–3

Опр: Медианой Ме(Х) – называется то её возможное значение, для которого выполняется равенство: Р(Х < Me(X)) = P(X > Me(X))

Функция распределения вероятностей случайной величины. Её свойства.

Для того, чтобы описать любую случайную величину (как дискретную, так и непрерывную) вводят понятие функции распределения вероятности.

Опр: Функцией распределения F(x) называют вероятность события в том, что случайная величина принимает значение меньше х, наперёд заданного.

Р ( Х < х) = F ( x )

Свойства F(x):

1) F(X) – неубывающая функция, т.е. F(X₂) ≥ F(X₁), при X₂ > X₁.

2) 0 ≤  F(X) ≤ 1

3) Вероятность того, что случайная величина х принимает свои возможные значения от a до b равна функции приращения на этом интервале, т.е.

P( a £ X £ b ) = F(b) – F(a).

4) Если случайная величина х принимает свои значения в интервале от a до b, то справедливо: F(X)=0, при x £ a и F(X)=1, при x ³ b.

замечание: если сл вел х принимает все знач, распределенные на оси ОХ, то справедливы соотношения:

 и .

Из свойств F(X) очевидно, как будут располагаться графики.

1) График F(X) для непрерывной случайной величины расположен в полосе между прямыми у=0 и у=1.

2) На промежутке (a,b) график поднимается.

3)Левее x=a ординаты графика равны 0, правее x=b ординаты графика равны 1.

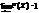Для ДСВ график F(X) ступенчатый