
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Плотность распределения вероятностей н.с.в. Её свойства. Мат ожидание, дисперсия и среднее квадратическое отклонение н.с.вНСВ, кроме функции распределения F(X), можно задать с помощью плотностью распределения. Опр: Плотность распределения вероятностей есть производная от функции распределения. f(x)=F’(x) По известной плотности распределения можно получить функцию распределения по следующей формуле: F(x) = –∞ ∫ x f(x) dx Свойства плотности распределения: 1) Плотность – есть функция неотрицательная (f(x)³0). 2) –∞ ∫ +∞ f(x) dx = 1 если a ≤ x ≤ b a ∫ b f(x) dx = 1 3) P (a < x < b) = a ∫ b f(x) dx
Опр: Мат ожидание НСВ X: M(X) = –∞ ∫ +∞ x∙f(x) dx где f(x) – плотность распределения. Опр: Дисперсия НСВ Х: D(X) = M(X 2) – M 2(X) = = –∞ ∫ +∞ x2 ∙ f(x) dx – (–∞ ∫ +∞ x ∙ f(x) dx)2 = –∞ ∫ +∞ (X–M(X))2 ∙ f(x) dx Опр: Средним квадратическим отклонением s(х) наз корень из дисперсии Центральные и начальные теоретические моменты н.с.в. Мода, медиана, асимметрия, эксцесс. Опр: Начальный теоретический момент порядка k НСВ Х, определяем по ф-ле: n2 = –∞ ∫ +∞ x∙f(x) dx Частный случай: n1=M(X), n2=M(X2), D(X)=n2-(n1)2. Опр: Центральным теоретич моментом порядка k НСВ Х, называется величина: mk = –∞ ∫ +∞ (X–M(X))k ∙ f(x) dx Частный случай: m1=0; m2=D(X)=n2-(n1)2; m3=n3-3n2n1+2(n1)3; m4=n4-4n3n1+6n2(n1)2-3(n1)4 Опр: Модой НСВ (М0(Х)) наз то ее возможное значение, которому соответствует локальный максимум плотности распределения. Зам: в частности, если f(x) имеет 2 max, то распределение наз-ся бимодальным. Опр: Медианой НСВ (Мe(Х)) называют то ее возможное значение х, в котором ордината плотности делит пополам площадь ограниченную кривой распределения, или медианой называют то возможное значение х, при котором P( X < Me ( X ) )=P ( X > Me ( X ) )  Опр: Асимметрией НСВ Х назыв отношение центрального теоретического момента 3-го порядка m3 к кубу среднего квадратического отклонения s3, т.е. As=m3/s3 Опр: Эксцессом сл вел Х назыв величина равная Ek = (m4/s4)–3
Равномерное распределение. Его числовые характеристики. Плотности распределений называют законами непрерывной случайной величины. Часто встречаются законы равномерного, показательного и нормального распределения. 1. Равномерное распределение. Опр: Распределение вероятности называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность сохраняет постоянное значение. Пусть случайная величина Х принимает все возможные значения на (a,b). Тогда по определению плотность примет вид (система): 0, x ≤ a f(x) = c, a < x < b 0, x ≥ b где с-const. Используя второе свойство плотности( –∞ ∫ +∞ f(x) dx = 1): a∫b c dx = 1; cx│ab ; c(b-a)=1; c=1/(b-a). Следовательно, закон равномерного распределения примет вид: 0 , x ≤ a f(x) = 1/(b–a) , a < x < b 0 , x ≥ b Интегрируя определённую выше плотность, получаем: 0 , x ≤ a F(x) = (x-a)/(b-a) , a < x < b 1 , x ≥ b Числовые характеристики равномерного распределения:
Показательное распределение. Его числовые характеристики. Показательное распределение(экспоненциальное): Опр: Показательным распределением НСВ Х назыв распределение, имеющее плотность вида: (система) 0, x < 0 f(x) = λe –λx , x ≥ 0
где l-некоторое положительное число(параметр)(l=const). График показательного распределения (1=λ):
Функция показательного распределения имеет вид: 0 , x < 0 F(x)=1– e – λx , x ≥ 0 График функции показательного распределения:
Числовые характеристики показательного распределения: M(X) = 1/λ D(X) = 1/λ2 σ(X) = 1/λ |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 449. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
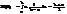 ;
; 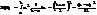 ;
; 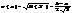
 .
.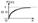 .
.