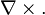Понятие потока вектора. Теорема Гаусса. Применение теоремы Гаусса для расчета симметрических полей.

Вычисление напряженности поля системы электрических зарядов с помощью при­нципа суперпозиции электростатических полей можно значительно упростить, ис­пользуя выведенную немецким ученым К. Гауссом (1777—1855) теорему, опреде­ляющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность.

В соответствии с формулой (79.3) по­ток вектора напряженности сквозь сфери­ческую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124),

Этот результат справедлив для замкнутой поверхности любой формы. Действитель­но, если окружить сферу (рис. 124) про­извольной замкнутой поверхностью, то каждая линия напряженности, пронизыва­ющая сферу, пройдет и сквозь эту по­верхность.

Если замкнутая поверхность произ­вольной формы охватывает заряд (рис. 125), то при пересечении любой вы­бранной линии напряженности с поверхно­стью она то входит в нее, то выходит из нее. Нечетное число пересечений при вы­числении потока в конечном счете сводит­ся к одному пересечению, так как поток считается положительным, если линии на­пряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверх­ность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в повер­хность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности лю­бой формы, если она замкнута и заключа­ет в себя точечный заряд Q, поток вектора Е будет равен Q/e₀, т. е.

Знак потока совпадает со знаком заряда Q. Рассмотрим общий случай произволь­ной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Е поля, создаваемо­го всеми зарядами, равна сумме напря-женностейЕ_i, создаваемых каждым за­рядом в отдельности:_;. Поэтому

Согласно (81.1), каждый из интегралов, стоящий под знаком суммы, равен Q_i/e₀. Следовательно,

Формула (81.2) выражает теорему Га­усса для электростатического поля в ваку­уме:поток вектора напряженности элек­тростатического поля в вакууме сквозь произвольную замкнутую поверхность ра­вен алгебраической сумме заключенных внутри этой поверхности зарядов, делен­ной на e₀. Эта теорема выведена матема­тически для векторного поля любой при­роды русским математиком М. В. Остро­градским (1801 —1862), а затем неза­висимо от него применительно к электро­статическому полю — К. Гауссом.

В общем случае электрические заряды могут быть «размазаны» с некоторой

объемной плотностью r=dQ/dV, различной

в разных местах пространства. Тогда сум­марный заряд, заключенный внутри замкнутой поверхности S, охватывающей не­который объем V,

Используя формулу (81.3), теорему Гаус­са (81.2) можно записать так:

Поле равномерно заряженной бесконечной плоскости.Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотно­стью+ s (s=dQ/dS—заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим ци­линдр, основания которого параллельны заря­женной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa=0), то поток вектора напряженности сквозь боковую повер­хность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания E_n совпадает с Е), т.е. равен 2ES. Заряд, заключенный внутри построенной цилин­дрической поверхности, равен sS. Согласно теореме Гаусса (81.2), 2ES = sS/e₀, откуда

Б 37

 Дивергенция, циркуляция, ротор вектора, их свойства. Теорема Стокса. Условие потенциальности. Теорема Остроградского- Гаусса. Теорема Гаусса в дифференциальной форме.

Дивергенция (от лат.divergere — обнаруживать расхождение) — дифференциальный оператор, отображающийвекторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток).

Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учётом знака. Поэтому можно дать более короткое определение дивергенции:

дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Оператор дивергенции, применённый к полю , обозначают как

или

Циркуля́циейве́кторногопо́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению

где — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, — бесконечно малое приращение радиус-вектора вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Обозначается

(в русскоязычной^[1] литературе) или

(в англоязычной литературе),

а также - как векторное умножение дифференциального оператора набла на векторное поле:

Результат действия этого оператора на конкретное векторное поле F называется ротором поляF или, короче, просто роторомF и представляет собой новое векторное^[2] поле:

Поле rotF (длина и направление вектора rotF в каждой точке пространства) характеризует в некотором смысле^[3] вращательную составляющую поля F соответственно в каждой точке