
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Электромагнитная индукция закон фарадея правило ленцаа) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится. б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра. Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек. Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток. Возникновение индукционного тока означает, что в контуре действует электродвижущая сила ?i – ЭДС I ЭДС индукции, возникающая в проводящем контуре, равна скорости изменения магнитного потока через площадь, ограниченную этим контуром – закон Фарадея.
В 1834 г. Э.Х. Ленц установил закон, позволяющий определить направление индукционного тока. Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Знак минус в законе Фарадея является математическим выражением правила Ленца. Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из N витков (например, соленоид), то если витки соединены последовательно, ?i будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности: 
Если Ф1 =Ф2=…=Фn, то
Т.к. ФB=BScosα, то для того чтобы изменить магнитный поток Ф можно изменить: 1) магнитное поле 2) площадь S; 3) угол α. Самоиндукция и взаимоиндукция ЭДС самоиндукции Изменяющийся по величине ток всегда создает изменяющееся магнитное поле, которое, в свою очередь, всегда индуктирует ЭДС. При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется ЭДС самоиндукции. Когда ЭДС в катушке индуктируется за счет изменения собственного магнитного потока, величина этой ЭДС зависит от скорости изменения тока. Чем больше скорость изменения тока, тем больше ЭДС самоиндукции. Величина ЭДС самоиндукции зависит также от числа витков катушки, густоты их намотки и размеров катушки. Чем больше диаметр катушки, число ее витков и густота намотки, тем больше ЭДС самоиндукции. Эта зависимость ЭДС самоиндукции от скорости изменения тока в катушке, числа ее витков и размеров имеет большое значение в электротехнике. Направление ЭДС самоиндукции определяется по закону Ленца. ЭДС самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока. Иначе говоря, убывание тока в катушке влечет за собой появление ЭДС самоиндукции, направленной по направлению тока, т. е. препятствующей его убыванию. И, наоборот, при возрастании тока в катушке возникает ЭДС самоиндукции, направленная против тока, т. е. препятствующая его возрастанию. Не следует забывать, что если ток в катушке не изменяется, то никакой ЭДС самоиндукции не возникает. Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку с железным сердечником, так как железо значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции при его изменении. ЭДС взаимоиндукции Итак, мы знаем, что ЭДС индукции в катушке можно вызвать и не перемещая в ней электромагнит, а изменяя лишь ток в его обмотке. Но что чтобы вызвать ЭДС индукции в одной катушке за счет изменения тока в другой, совершенно не обязательно вставлять одну из них внутрь другой, а можно расположить их рядом И в этом случае при изменении тока в одной катушке возникающий переменный магнитный поток будет пронизывать (пересекать) витки другой катушки и вызовет в ней ЭДС.
Взаимоиндукция дает возможность связывать между собой посредством магнитного поля различные электрические цепи. Такую связь принято называть индуктивной связью. Величина ЭДС взаимоиндукции зависит прежде всего от того, с какой скоростью изменяется ток в первой катушке. Чем быстрее изменяется в ней ток, тем создается большая ЭДС взаимоиндукции. Кроме того, величина ЭДС взаимоиндукции зависит от величины индуктивности обеих катушек и от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Следовательно, различные по своей индуктивности и взаимному расположению катушки и в различной среде способны вызывать одна в другой различные по величине ЭДС взаимоиндукции. Чтобы иметь возможность различать между собой различные пары катушек по их способности взаимно индуктировать ЭДС, введено понятие о взаимоиндуктивности или коэффициенте взаимоиндукции. Обозначается сявзаимоиндуктивность буквой М. Единицей ее измерения, так же как и индуктивности, служит генри. Генри — это такаявзаимоиндуктивность двух катушек, при которой изменение тока в одной катушке на 1 ампер в 1 секунду вызывает в другой катушке ЭДС взаимоиндукции, равную 1 вольту. На величину ЭДС взаимоиндукции влияет магнитная проницаемость окружающей среды. Чем больше магнитная проницаемость среды, по которой замыкается переменный магнитный поток, связывающий катушки, тем сильнее индуктивная связь катушек и больше величина ЭДС взаимоиндукции. На явлении взаимоиндукции основана работа такого важного электротехнического устройства, как трансформатор. 29. Вихревое электрическое поле. Ток смещения. Уравнения Максвелла Как мы знаем из закона электромагнитной индукции Фарадея, в замкнутом контуре индуцируется ЭДС при изменении магнитного потока, пронизывающего этот контур
Если контур (проводник) движется, то причиной возникновения ЭДС может быть сила Лоренца. Если же контур неподвижен, то и в этом случае, как показывает опыт, в нём возникает ЭДС, определяемая уравнением (3.93). Какова же в этом случае причина возникновения ЭДС? Под действием ЭДС в контуре возникает электрический ток. Это значит, что на электроны проводника действует электрическое поле. Если контур жёсткий, то можно записать
или
(Мы поставили знак частной производной, поскольку магнитная индукция может зависеть и от координаты и от времени.) Из 14.2 следует, что циркуляция этого поля по замкнутому контуру не равна нулю, в отличие от электростатического поля. Максвелл предположил, что изменяющееся во времени магнитное поле порождает вихревое электрическое поле, независимо от того, имеется у нас проводящий контур или нет. Просто если он есть, то позволяет зарегистрировать вихревое электрическое поле ЕВ. Левую часть уравнения (3.94) можно преобразовать по формуле Стокса
Поскольку интегрирование может производиться по любой поверхности, опирающейся на контур L, то в каждой точке этой поверхности должны равняться подынтегральные выражения
Поле ЕВ существенно отличается от электростатического поля, для которого, как мы помним, циркуляция по замкнутому контуру равна нулю:
В общем случае
но для ротора суммарного поля, в силу уравнения (3.97), остаётся справедливым соотношение (3.96). Таким образом,
Поскольку переменное магнитное поле порождает электрическое, как это следует из закона индукции Фарадея и полученной нами из этого закона формулы (3.99), то должно существовать и обратное явление – переменное электрическое поле должно порождать магнитное поле. Для установления количественных соотношений рассмотрим процесс заряда конденсатора.
D=s . (3.100) Здесь s – поверхностная плотность зарядов на обкладке конденсатора. Как мы уже говорили, Максвелл предположил, что изменяющееся электрическое поле создаёт магнитное поле. Но мы знаем, что постоянное магнитное поле создаётся токами. Поэтому естественно предположение, что должен быть ещё один ток, который Максвелл назвал током смещения и который ответственен за создание магнитного поля. Для установления вида этого тока смещения, рассмотрим соотношение (3.100) справа налево, а именно s =D. (3.101) Умножим обе части на площадь пластины S и получим q=sS= DS. (3.102) Здесь q – заряд пластины конденсатора. Во время заряда конденсатора ток в подводящем проводе
Разделив обе части последнего уравнения на площадь пластины S, получим слева ток проводимости j=I/S, а справа – плотность нового, максвелловского тока, или плотность тока смещения. Таким образом,
В последнем уравнении мы поставили значки векторов – для общего случая и написали частную производную, поскольку в общем случае вектор электрического смещения может зависеть и от координаты. Проанализировав полученные результаты, Максвелл ввёл понятие общего тока как суммы токов проводимости и тока смещения. Здесь подчеркнём, что ток смещения – это просто название изменяющегося во времени электрического поля. Единственная функция тока смещения – создавать магнитное поле. Тогда обобщенный закон полного тока будет иметь вид
или окончательно
Максвелл создал замкнутую макроскопическую теорию электромагнитного поля. В основе этой теории лежат его знаменитые уравнения. Первая пара связывает основные характеристики электрического и магнитного полей
В уравнении (3.107) под полем E надо понимать полное поле – поле, созданное неподвижными зарядами, и поле, созданное изменяющимся магнитным полем. Уравнение (3.108) отражает тот факт, что в природе нет магнитных зарядов. Вторая пара уравнений Максвелла связывает вспомогательные характеристики электрического и магнитного полей
Вихревое электрическое поле (первое уравнение Максвелла) Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году. Максвелл проанализировал все известные к тому времени законы электродинамики и сделал попытку применить их к изменяющимся во времени электрическому и магнитному полям. Он обратил внимание на асимметрию взаимосвязи между электрическими и магнитными явлениями. Максвелл ввел в физику понятие вихревого электрического поля и предложил новую трактовку закона электромагнитной индукции, открытой Фарадеем в 1831 г.: Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Максвелл высказал гипотезу о существовании и обратного процесса (о природе сторонних сил): Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле. Гипотеза Максвелла была лишь теоретическим предположением, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, т. е. систему уравнений электромагнитного поля (уравнений Максвелла). Обозначим напряженность поля сторонних сил
Подставим это в закон Фарадея
Для неподвижных контура и поверхности операции дифференцирования и интегрирования можно поменять местами
Переменное магнитное поле создает в любой точке пространства вихревое электрическое поле независимо от того, находится в этой точке проводник или нет. Ранее для электростатического поля было показано
Ток смещения (второе уравнение Максвелла) Максвелл предположил, что между электрическим и магнитным полями существует и обратная связь: если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то и всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для описания переменного электрического поля Максвелл ввел понятие тока смещения. Ток смещения между обкладками конденсатора равен току проводимости в цепи. Теорема Гаусса
Плотность тока смещения в данной точке пространства равна скорости изменения вектора электрического смещения в этой точке. Ток смещения существует и в проводнике, он не разделим пространственно с током проводимости, поэтому Максвелл ввел понятие полного тока (I + Iсм). Закон полного тока:
– второе уравнение Максвелла. (5) |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 961. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 индукции.
индукции.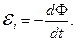

 - потокосцепление или полный магнитный поток.
- потокосцепление или полный магнитный поток.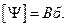
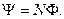
 ;
; . (3.93)
. (3.93) ,
, . (3.94)
. (3.94) . Тогда, вместо уравнения (3.94), получим
. Тогда, вместо уравнения (3.94), получим . (3.95)
. (3.95) . (3.96)
. (3.96) , а значит, в соответствии с теоремой Стокса, и ротор этого поля в любой точке равен нулю:
, а значит, в соответствии с теоремой Стокса, и ротор этого поля в любой точке равен нулю: . (3.97)
. (3.97) , (3.98)
, (3.98) . (3.99)
. (3.99) Для начала определим поле вблизи поверхности металлической обкладки конденсатора. Применим терему Гаусса для вектора электрического смещения к одной из обкладок (рис. 3.21). Внутри металла поле равно нулю, а снаружи направлено перпендикулярно поверхности. Следовательно, поток через весь цилиндр сведётся к потоку через верхнее основание цилиндра площадью dS. И этот поток должен равняться заряду, заключённому внутри нашего цилиндра, или DdS=sdS, или
Для начала определим поле вблизи поверхности металлической обкладки конденсатора. Применим терему Гаусса для вектора электрического смещения к одной из обкладок (рис. 3.21). Внутри металла поле равно нулю, а снаружи направлено перпендикулярно поверхности. Следовательно, поток через весь цилиндр сведётся к потоку через верхнее основание цилиндра площадью dS. И этот поток должен равняться заряду, заключённому внутри нашего цилиндра, или DdS=sdS, или . (3.103)
. (3.103) . (3.104)
. (3.104) , (3.105)
, (3.105) . (3.106)
. (3.106) ; (3.107)
; (3.107) . (3.108)
. (3.108) ; (3.109)
; (3.109)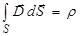 . (3.110)
. (3.110) , тогда по определению ЭДС это работа, которую затрачивают сторонние силы на перемещение единичного положительного заряда с (-) клеммы на (+) клемму внутри источника
, тогда по определению ЭДС это работа, которую затрачивают сторонние силы на перемещение единичного положительного заряда с (-) клеммы на (+) клемму внутри источника



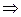
 . (2)
. (2) – первое уравнение Максвелла. (3)
– первое уравнение Максвелла. (3) , т.е. поле потенциально, его силовые линии разрывные, они начинаются и заканчиваются на зарядах. Из первого уравнения Максвелла видно, что циркуляция ЕВ не равна нулю, электрическое поле (и связанное с ним магнитное поле не потенциальные - вихревые). Силовые линии ЕВ замкнуты в отличие от силовых линий кулоновского поля Е.
, т.е. поле потенциально, его силовые линии разрывные, они начинаются и заканчиваются на зарядах. Из первого уравнения Максвелла видно, что циркуляция ЕВ не равна нулю, электрическое поле (и связанное с ним магнитное поле не потенциальные - вихревые). Силовые линии ЕВ замкнуты в отличие от силовых линий кулоновского поля Е.





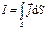
 ,
,  . (4)
. (4)


