
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оптимизация при наличии ограничений. ⇐ ПредыдущаяСтр 7 из 7
Рассмотренные выше экспериментально-статистические методы оптимизаци предусматривают планомерное изменение факторов варьирования (управляющих параметров) Ограничение диапазона варьирования переменных
Входные параметры xi также имеют ограничения
Ограничения (1) и (2) выделяют в факторном пространстве
 
Рис.27. Формирование области допустимых значений для двухфакторного процесса.
Концентрические кривые показывают линии равных значений целевой функции, т.е. Экстремальная точка может лежать не только внутри, но и за пределами допустимой области. В этом случае задача сводится к отысканию точки Задача оптимизации при наличии ограничений формулируется следующим образом: необходимо найти координаты максимума целевой функции
т. е. найти Применение метода крутого восхождения для решения сформулированной задачи не может привести к положительным результатам, т. к. его алгоритм не учитывает наложенных на вход процесса ограничений. Как правило, при наличии ограничений движение по Рассмотрим процедуру эксперимента для нахождения точки
Ограничения (5) и (6) наложены непосредственно на значения варьируемых параметров, а ограничения (7) – на значения выходного показателя На первом этапе поиска проводится полный факторный эксперимент с центром в начальной точке Статистическая обработка результатов ПФЭ также выполняется по стандартной схеме, т. е. проверяется воспроизводимость опытов, значимость коэффициентов b0, b1, b2 уравнения регрессии, адекватность линейной модели
Если при осуществлении факторного эксперимента ни в одной из пробных точек ограничения (5), (6) и (7) не были нарушены, то из центра планирования Для того чтобы величина градиента
Затем, как обычно, рассчитывается траектория мысленного движения к оптимуму, и в некоторых точках Крутое восхождение прекращается в следующих случаях 1. Если значение целевой функции проходит через экстремум и начинает убывать (при поиске максимального значения) или возрастать (при поиске минимального значения). 2. Если нарушается ограничение типа (7), тогда для корректировки направления движения ставится новый факторный эксперимент с центром в точке За новый центр планирования
где
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 339. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , пока не будет достигнут экстремум целевой функции в некоторой точке
, пока не будет достигнут экстремум целевой функции в некоторой точке  , т.е.
, т.е.  . Однако при оптимизации конкретных технологических процессов и конструкций часто могут встречаться такие комбинации управляющих параметров, которые нежелательны по техническим или экономическим показателям.
. Однако при оптимизации конкретных технологических процессов и конструкций часто могут встречаться такие комбинации управляющих параметров, которые нежелательны по техническим или экономическим показателям. связано, прежде всего, с тем, что в условиях реального технологического процесса (или объекта) наряду с целевой функцией
связано, прежде всего, с тем, что в условиях реального технологического процесса (или объекта) наряду с целевой функцией  имеется ряд контролируемых выходных параметров
имеется ряд контролируемых выходных параметров  (где L = II,III,…,G), также зависящих от k-мерного вектора управляющих воздействий
(где L = II,III,…,G), также зависящих от k-мерного вектора управляющих воздействий  . Обычно аналитическая форма этих зависимостей, как и характер целевой функции
. Обычно аналитическая форма этих зависимостей, как и характер целевой функции  и
и 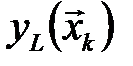 в каждой точке
в каждой точке 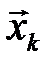 факторного пространства могут быть определены только экспериментально. На значения контролируемых входных параметров
факторного пространства могут быть определены только экспериментально. На значения контролируемых входных параметров 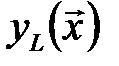 обычно накладываются ограничения
обычно накладываются ограничения ; L = II,III,…,G, (1)
; L = II,III,…,G, (1) ; L = II,III,…,G.
; L = II,III,…,G. , i = 1,2,…,k. (2)
, i = 1,2,…,k. (2) область допустимых значений вектора управляющих параметров
область допустимых значений вектора управляющих параметров  . На рисунке 27 приведен пример формирования области допустимых значений
. На рисунке 27 приведен пример формирования области допустимых значений  для двухфакторного процесса.
для двухфакторного процесса.

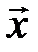
 . Так как ограничения (1) задаются в виде неравенства
. Так как ограничения (1) задаются в виде неравенства  , то в факторном пространстве
, то в факторном пространстве  ; L = II,III,…,G (кривые со штриховкой на рис. 27). Поверхности ограничения, пересекаясь, выделяют в факторном пространстве область Dk допустимых значений
; L = II,III,…,G (кривые со штриховкой на рис. 27). Поверхности ограничения, пересекаясь, выделяют в факторном пространстве область Dk допустимых значений  условного экстремума функции уI на границе области допустимых значений Dk.
условного экстремума функции уI на границе области допустимых значений Dk.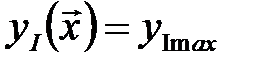 на подмножестве всех
на подмножестве всех  ;
;  ; L = II,III,…,G (3)
; L = II,III,…,G (3)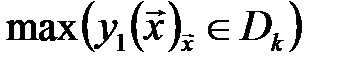 .
. приходится сочетать с движением вдоль границы.
приходится сочетать с движением вдоль границы. в факторном пространстве двух переменных х1 и х2, отвечающую условиям
в факторном пространстве двух переменных х1 и х2, отвечающую условиям (4)
(4) (5)
(5) (6)
(6) (7)
(7) , которые определяются только из опыта.
, которые определяются только из опыта. . Он проводится аналогично эксперименту при методе крутого восхождения. Но в отличие от последнего в экспериментальной точке
. Он проводится аналогично эксперименту при методе крутого восхождения. Но в отличие от последнего в экспериментальной точке  измеряются не только значения целевой функции
измеряются не только значения целевой функции  , но и контролируемого параметра
, но и контролируемого параметра  .
. (8)
(8) .
. не зависела от скорости возрастания функции
не зависела от скорости возрастания функции  в точке
в точке  , его составляющие следует пронормировать
, его составляющие следует пронормировать ;
;  (9)
(9) этой траектории (обычно через 2-3 мысленных шага) проводится измерение отклика
этой траектории (обычно через 2-3 мысленных шага) проводится измерение отклика  . При этом обязательно проверяется значение контролируемого параметра
. При этом обязательно проверяется значение контролируемого параметра  .
. .
. в первом случае принимается точка, где целевая функция имела экстремальное значение, во втором – последняя из точек факторного пространства, где был реализован мысленный опыт, и еще не нарушалось ограничение (7). Если причиной останова послужило нарушение ограничения (7), то следующий цикл крутого восхождения проводится по компромиссному направлению, которое выбирается таким образом, чтобы точка
в первом случае принимается точка, где целевая функция имела экстремальное значение, во втором – последняя из точек факторного пространства, где был реализован мысленный опыт, и еще не нарушалось ограничение (7). Если причиной останова послужило нарушение ограничения (7), то следующий цикл крутого восхождения проводится по компромиссному направлению, которое выбирается таким образом, чтобы точка  , (10)
, (10) – вектор, нормальный к эквипотенциальной поверхности (поверхности равного уровня)
– вектор, нормальный к эквипотенциальной поверхности (поверхности равного уровня)  в точке
в точке  (рис. 28).
(рис. 28).