Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы подбора эмпирических формул
Эмпирические формулы – это приближенные значения аналитических формул или формулы, описывающие закономерности результатов эксперимента. На основании экспериментальных данных можно подобрать алгебраическое выражение функции
которое называется эмпирической формулой в пределах измеренных значений аргументов х1…хn. Замену точных выражении приближенными, более простыми называют аппроксимацией, а сами функции – аппроксимирующими. Они имеют ограниченную область применения, которая не должна выходить за пределы опытных данных, т.е. по ним надёжно можно проводить только интерполяцию, но не экстраполяцию. Процесс подбора эмпирических формул состоит из следующих этапов. 1) Данные измерений наносят на сетку прямоугольных координат; по экспериментальным точкам проводят плавную кривую и выбирают ориентировочно вид формулы. 2) Вычисляют параметры формулы, которые наилучшим образом соответствовали бы принятой формуле и результатам измерений. Подбор необходимо начинать с уравнения прямой линии
где b0, b1 – постоянные коэффициенты. Оно представляет собой простое выражение. Поэтому при анализе графического материала необходимо по возможности использовать линейную функцию. Если в равномерных координатах экспериментальные данные ложатся в виде кривой, то применяют метод выравнивания, т.е. кривую представляют в виде линейной функции
где Далее строят прямую в координатах «X-Y», по которой вычисляют параметры b0, b1 (рис.14).
  Рис.14. Выравнивание нелинейной зависимости
Прямую целесообразно проводить, используя метод наименьших квадратов, т.е. для лучшей прямой сумма квадратов отклонений εi от прямой должна быть наименьшей
Для облегчения и упрощения расчётов часто используется метод нулевых средних, когда
Когда экспериментальная кривая на равномерной сетке прямоугольных координат имеет плавный вид, целесообразно использовать графический метод выравнивания. Рассмотрим некоторые характерные кривые, их функциональные зависимости и способы выравнивания. На рис.15 представлены 4 вида кривых. Кривые вида 1 могут быть аппроксимированы зависимостью
Логарифмируя правую и левую часть, получаем
Или в новой системе координат
где

Рис.15. Характерные кривые для графического выравнивания
Однако графическое выравнивание (спрямление) с помощью логарифмических сеток можно использовать, когда значение аргумента X > 0 и X ≠ 1. Пример: В результате эксперимента получены следующие данные
где yэ – экспериментальные значения; y – расчётные значения по зависимости
Приведённая зависимость получена следующим образом. На график в равномерной системе координат «х-у» наносятся экспериментальные точки «х-уэ». Проводят визуальную графическую обработку и определяют значение двух крайних точек у. Для нахождения параметров а и b составляют и решают систему уравнений
откуда b = 0,331, а = 0,4945. Кривая 2 может быть аппроксимирована зависимостью
После логарифмирования получаем
или т.е. спрямление реализуется в полулогарифмической системе координат (логарифмическая сетка по оси Y и равномерная – по х). Пример:
Система уравнений по двум крайним точкам, полученным после графической обработки экспериментальных данных.
т.е. b = 0,5843, а = 8,475, Кривые типа 3 аппроксимируются зависимостью
Замена
Кривые типа 4 аппроксимируются зависимостью
Изменяя сетку по оси «у» на
При подборе эмпирических формул широко используется полином типа
где b0, b1, b2 ... bn – постоянные коэффициенты. Полиномами можно аппроксимировать любые результаты измерений, если они графически выражаются непрерывными функциями. Для определения коэффициентов «b», кроме графического метода, применяют также метод средних отклонений и метод наименьших квадратов. Рассмотрим более подробно эти методы.
13.3. Метод средних отклонений
Метод средних отклонений основан на следующем положении. По экспериментальным данным (точкам) можно построить множество плавных, кривых. Наилучшей будет та кривая, у которой сумма разностных отклонений будет равна нулю, т.е.
Порядок расчёта коэффициентов полинома состоит в следующем. Экспериментальные данные изменения «у» от «х» заносят в таблицу, строится диагональная таблица тех разностей, которые можно принять постоянными. Например, для семи экспериментальных точек диагональная таблица разностей имеет следующий вид.
Определяется число ряда и степень полинома «n». Обычно берётся n = 3...4. В принятый полином последовательно подставляются координаты х и у нескольких экспериментальных точек (m). Получают систему из «m» уравнений, линейных относительно неизвестных коэффициентов «b». Каждое уравнение приравнивается соответствующему отклонению ε, которое представляет собой разность между экспериментальным и расчётным значением «у» (рис. 16). Число точек «m» должно быть больше степени полинома «n», т.к. иначе система уравнений не решается. Если m значительно больше n, то сначала разбивают все уравнения на n+1 группы по мере увеличения переменной х. В каждой группе складывают уравнения и получают новую систему уравнений, равную n+1 групп.

Рис.16. Экспериментальные точки и аппроксимирующая кривая
Решая систему линейных уравнений, определяют коэффициенты «b» аппроксимирующего полинома. Метод средних обладает высокой точностью при большом числе точек (m > 4).
Пример
Таблица 6
Выбираем полином второй степени
Разбиваем систему из 7 уравнений на 3 группы, считая, что внутри групп также действует принцип
где к - количество уравнений в группе. Тогда, суммируя уравнения в каждой группе, получаем систему из 3-х уравнений с 3-я неизвестными коэффициентами b0, b1, b2.
Решая уравнения относительно коэффициентов b0, b1, b2 и подставляя их значения в выбранный полином, получаем
Результаты расчета значений «y» по аппроксимирующему полиному приведены в таблице 6. Метод средних может также быть применён для различных кривых после их выравнивания (спрямления).
Пример
Таблица 7
Анализ представленной в виде таблицы зависимости в прямоугольной системе координат дает возможность аппроксимировать ее зависимостью
или
где Так как необходимо определить только 2 параметра (А, b), то все результаты измерений делим на 2 группы:
Решая систему из двух уравнений, получаем Расчетные значения y приведены в табл.7.
Метод наименьших квадратов
Метод нулевых средних отклонений не даёт единственного решения, т.к. его результаты зависят от способа группирования экспериментальных данных. Это вызывает некоторую неопределённость. Указанного недостатка лишён метод наименьших квадратов. Суть его заключается в том, что если все измерения функции
т.е. сумма квадратов отклонении измеряемых значении от расчетных принимает наименьшее значение. При этом получается только одно решение (формула) – лучшая из всех возможных. Некоторый недостаток метода наименьших квадратов состоит в том, что он трудоёмок при большом числе начальных уравнений. Рассмотрим сущность метода наименьших квадратов на примере, когда
где yi – значение функции для аргумента xi, рассчитанное по аппроксимирующему полиному; yiэ – экспериментальное значение функции при аргументе xi; εi – отклонение экспериментального (измеренного) значения функции от расчетного при аргументе xi. Подставив экспериментальные значения хiэ и уiэ в выбранное уравнение и возведя в квадрат правые и левые части, получаем
Просуммируем левые и правые части приведённой выше системы уравнений
Если переменными величинами считать коэффициенты b0, b1, b2, b3, то условие минимума приведённого выражения
Возьмём частные производные по b0, b1, b2, b3
Последние уравнения называются нормальными. Их можно записать по-другому. Для этого раскроем скобки каждого уравнения и просуммируем слагаемые с одинаковыми коэффициентами. После преобразований получаем
Таким образом, имеется 4 нормальных уравнения для нахождения 4-х неизвестных коэффициентов, т.е. по отношению к коэффициентам «b» имеем систему линейных уравнений. Для полинома 2-й степени система нормальных уравнений имеет следующий вид.
Соответственно для прямой линии имеем 2 уравнения с 2-мя неизвестными b0, b1.
Пример m = 6, n = 1 Таблица 8
Графическая обработка экспериментальных данных показала, что они могут быть аппроксимированы прямой линией
Тогда
Решаем эту систему относительно b0, b1, получим b0 = –0,57, b1 = 2,192, т.е.
Обработка результатов эксперимента по методу средних отклонений даёт уравнение прямой следующего вида:
Если результаты эксперимента аппроксимировать параболой 2-й степени, то её уравнение будет
ПЛАНИРОВАНИЕ И ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОФАКТОРНОГО ЭКСПЕРИМЕНТА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 446. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
, ,
, ,
, ;
;  , т.е. новые оси координат имеют не равномерную, а функциональную сетку.
, т.е. новые оси координат имеют не равномерную, а функциональную сетку. (или Yi при X = 0)
(или Yi при X = 0) .
.

 .
. .
. .
. .
. ,
,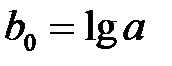 ,
,  , т.е. на двойной логарифмической сетке будет прямая линия, у которой
, т.е. на двойной логарифмической сетке будет прямая линия, у которой .
.
 .
. или
или  ,
, .
. ,
,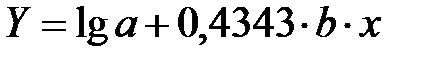 ,
,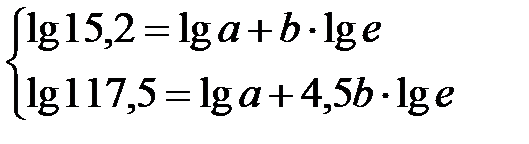 или
или  ,
, .
. .
. даёт прямую линию на сетке прямоугольных координат (y-X)
даёт прямую линию на сетке прямоугольных координат (y-X)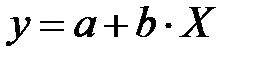 .
. .
. , получаем прямую линию в системе координат «х-У» , т.е. по оси х сетка не изменяется
, получаем прямую линию в системе координат «х-У» , т.е. по оси х сетка не изменяется .
. ,
, .
.











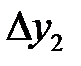
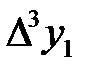



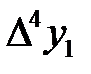





















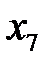

 .
.




 .
. ,
,

 или
или
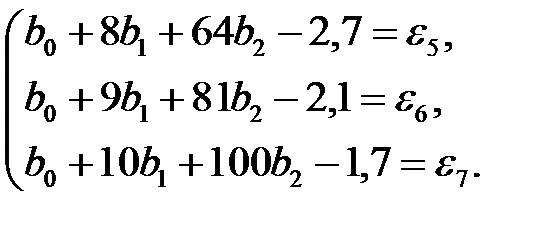
 .
. ,
,
 ,
, ,
,  ,
, 
 ;
;
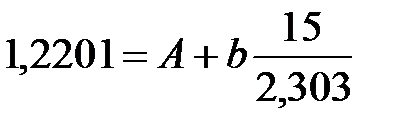 ;
;
 ;
;
 ;
;
 ;
;
 ;
;




 ,
, 
 , тогда
, тогда  .
. проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия.
проведены с одинаковой точностью и ошибки измерений распределяются по нормальному закону, то параметры выбранного аппроксимирующего уравнения однозначно определяются из условия.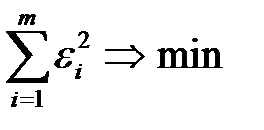 ,
, , а их количество m >> 4. Тогда для каждой точки
, а их количество m >> 4. Тогда для каждой точки ,
,  ,
, .
.
 будет
будет




 . Составим нормальные уравнения.
. Составим нормальные уравнения.