
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методика работы над заданиямиСтохастического характера В содержании стохастической содержательно-методической линии выделяются (Г.С. Евдокимова, А. Плоцки, В.Д. Селютин, С.А. Самсонова и др.) три взаимосвязанных направления, методикой работы над которыми должен владеть будущий учитель: - подготовка младших школьников в области комбинаторики, с целью создания в дальнейшем аппарата для решения вероятностных задач и логического развития учащихся; - формирование первоначальных представлений о случайных событиях, о вероятностях событий; - подготовка в области математической статистики: формирование умений, связанных с представлением, сбором данных и их интерпретацией. Методика работы над заданиями Комбинаторного характера Профессиональная компетентность учителя в области обучения младших школьников комбинаторике характеризуется: - знанием познавательного значения стохастики и необходимости ее изучения в школе; - владением основными методами решения стохастических задач в начальной школе; - пониманием сущность пропедевтики изучаемого материала; - умением обеспечить мотивацию учебной деятельности младших школьников; - умением сравнивать школьный и вузовский варианты изложения материала; - умением осуществлять в обучении моделирование; - умением работать с учебной, методической и научной литературой по комбинаторике, теории вероятностей и математической статистике; - владением навыками самостоятельной работы. Проблему введения в начальный курс математики элементов стохастики рассматривают многие методисты. Работе над задачами стохастического характера уделяется достаточно большое внимание такими методистами, как Т. Е. Темерязев, С. А. Козлова, А. Г. Рубина, А. П. Тонких, труды которых направлены на разработку программ по математике в рамках образовательной системы «Школа 2100».  В учебниках «Моя математика», выделяется целая линия, посвященная решению проблемы введения элементов стохастики в начальный курс математики, которая называется: «Элементы стохастики». Она является обязательной и построена, как и традиционные содержательные линии, но в то же время обладает своей спецификой. Уже в 1-ом классе дети знакомятся с чтением и записью информации в таблицах, даются первоначальные представления о графах[12]. По мнению методистов и психологов, включение комбинаторных задач в начальный курс математики оказывает положительное влияние на развитие младших школьников. Решение комбинаторных задач дает возможность расширить знания учащихся о самой задаче, например, о количестве и характере результата, о процессе решения задачи (чтобы ее решить вовсе не обязательно выполнять какие-либо арифметические действия). Рассмотрим такой пример. Из цифр числа 246, нужно составить всевозможные двузначные числа так, чтобы цифры в записи числа не повторялись: 24, 26, 42, 62, 64, 42, 46. В процессе решения данной задачи с одной стороны задействована такая мыслительная операция, как анализ – расчленение целого на части, выделение отдельных элементов в объекте. С другой – проводится синтез, то есть соединение элементов, объектов в единое целое: 24, 26, 42, 46, 62, 64. Решая задачу путем систематического перебора, учащимся приходится производить классификацию объектов, то есть соотносить признаки объектов. В результате чего происходит обобщение – выделение существенных признаков объектов, а также объединение объектов на основе этих признаков. Кроме того, в процессе выполнения таких заданий с множеством цифр числа младшие школьники повторяют устную и письменную нумерацию, работают над разрядным составом чисел, обращают внимание на поместное значение цифр, постоянно различают понятия «число» и «цифра». Таким образом, систематическое использование комбинаторных задач при рассмотрении математических понятий одновременно способствует реализации развивающих и образовательных функций курса «Математика в начальной школе»[13]. Опыт работы показывает, что начальный курс математики должен включать в себя предварительное знакомство учащихся с комбинаторными задачами и методами их решения, естественно, на соответствующем уровне. Учащимся начальных классов, как правило, приходится решать задачи на упорядочивание элементов некоторого множества, на образование и подсчет числа кортежей заданной длины, составленных из элементов некоторого множества; задачи в которых требуется осуществить выбор подмножеств с определенными свойствами. В основе способов решения подобных задач лежат правило суммы и правило произведения, хотя они обычно в явном виде младшим школьникам не формулируются. Анализ существующих учебников математики для начальной школы показывает, что многие комбинаторные задачи носят практическую направленность, основаны на реальном сюжете. Это вызвано психологическими особенностями младших школьников уровнем развития их мышлением. В этой связи система упражнений строится таким образом, чтобы был обеспечен постепенный переход от работы с множеством объектов к действиям в уме. Комбинаторные задачи решают различными методами, условно разделенными на «формальные» и «неформальные». При «формальном» методе решения нужно определить характер выбора, выбрать соответствующую формулу или комбинаторное правило (правило суммы или произведения), подставить числа и вычислить результат, представленный количеством возможных вариантов выбора, сами же варианты в этом случае не образовываются. При «неформальном» методе решения задач на первый план выходит процесс составления различных вариантов. Главное уже не количество составленных вариантов выбора, а какие варианты выбора могут получаться. «Неформальным» является метод перебора. Он доступен младшим школьникам и позволяет накапливать опыт решения конкретных задач, что служит основой для введения в дальнейшем обучении комбинаторных и принципов решения заданий и использования соответствующих формул. В практической деятельности человеку приходиться не только определять число возможных вариантов выбора, но и непосредственно составлять все эти варианты, а, владея приемами систематического перебора, это можно сделать более рационально. Комбинаторные задачи, решаемые методом перебора, должны удовлетворять принципу полноты. Совокупность задач, предлагаемых для решения, должна учитывать психологические особенности младших школьников и удовлетворять принципу «от простого, к сложному», то есть способ перебора должен постепенно усложняться. Решение комбинаторных задач методом перебора осуществляется в зависимости от степени сложности осуществления перебора. В связи с этим методисты (С. А. Козлова, А. Г. Рубина, А. П. Тонких, О. С. Медведева) различают следующие группы задач: – задачи, в которых нужно произвести полный перебор всех возможных вариантов; – задачи, в которых использовать прием полного перебора не целесообразно и нужно исключить некоторые варианты, не рассматривая их (то есть осуществить сокращенный перебор); – задачи, в которых операция перебора производится несколько раз и по отношению к разного рода объектам. Пример 1.Четыре яхты готовились к соревнованиям. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, как по-разному раскрасили паруса, если было всего две краски: синяя и красная.
Основная трудность, которая возникает у младших школьников при раскрашивании – это догадаться, что весь парус можно закрасить одним цветом. Поэтому, после того как учащиеся раскрасят 2 паруса двумя цветами:
Пример2.Составьте все возможные выражения, расставляя знаки «+» и «–» между числами 3, 5, 7. Проводится полный перебор вариантов: – последовательность двух знаков в выражении может быть одинаковой, тогда получаем 3 + 5 + 7, 3 – 5 – 7; – последовательность двух знаков в выражении может быть различной, тогда получаем 5 + 6 – 7, 5 – 6 + 7. Затем учитель может предложить учащимся найти значения составленных выражений и ответить на вопрос: «В каких случаях значения числовых выражений имеют смысл, а в каких – нет?». Пример 3.Три кассира хранят деньги в сейфе, на котором три замка. Кассиры хотят распределить между собой ключи от замков так, чтобы сейф мог открываться только в присутствии хотя бы двух кассиров, но не одного. Как это можно сделать? Перебираются все возможные случаи распределения ключей. Каждому кассиру можно дать по одному ключу или по два разных ключа, или по три. 1) Предположим, что у каждого кассира по 1 ключу, тогда, если придут любые двое из них, то они не смогут открыть сейф. 2) У каждого кассира по три разных ключа. Тогда сейф сможет открыть один кассир, а это не соответствует условию. 3) Дадим каждому кассиру по два разных ключа. Первому дадим 1 и 2 ключи, второму – 1 и 3 ключи, третьему – 2 и 3 (осуществляется выбор из 3 типов ключей по 2 ключа). Проверим ситуацию, когда придут любые два кассира, смогут ли они открыть сейф. Рассматриваются все возможные случаи: могут прийти первый и второй кассиры, у них будут все ключи (1 и 2, 1и 3); могут прийти первый и третий кассиры, у них также будут все ключи (1 и 2, 2 и 3); могут прийти второй и третий кассиры, у них тоже будут все ключи (1 и 3, 2 и 3). Таким образом, чтобы найти ответ в задачи, нужно выполнить операцию перебора несколько раз. В процессе решения аналогичных задач младшие школьники вначале приобретают опыт хаотичного перебора возможных вариантов, а затем, на основе этого опыта, осуществляют систематический перебор всех возможных вариантов. Методика обучения учащихся решению комбинаторных задачам и заданий комбинаторного характера предусматривает три этапа работы. На первом этапе при выполнении заданий комбинаторного характера младшие школьники составляют новые объекты, осуществляя хаотический перебор. Приобретение навыков такого типа в дальнейшем будет способствовать появлению более высокой ступени организации деятельности – использованию при решении заданий комбинаторного характера систематического перебора. На данном этапе учитель не ставит цели найти все варианты. Особое внимание уделяется сравнению объектов, которые состоят из отдельных элементов. Сравнение проводится по следующим критериям: – по количеству составленных объектов; – составу, входящих в объект элементов; – порядку расположения элементов в объекте. Примерами таких задач является задачи типа : 1. У Маши был мяч. Одна половинка мяча красная, другая – желтая, посередине проходят две полосы: синяя и зеленая. Нарисуйте, как при помощи этих цветов можно раскрасить мяч по-другому? 2. Даша решила посадить розу, тюльпан и ромашку. Нарисуйте, как можно посадить цветы в один ряд? 3. Имеется 3 кубика конструктора «Лего»: белый, желтый, зеленый. Нарисуйте несколько различных построек из этих кубиков. 4. Расставляя знаки «+» и «∙» между данными числами 11, 8, 5, составь все возможные выражения. Следующий этап состоит в нахождении учащимися всех возможных вариантов решения комбинаторных задач. Цель данного этапа – обучение школьников систематическому перебору всех возможных вариантов. При решении задач на данном этапе можно осуществлять как полный, так и сокращенный перебор. Приведем примеры задач, при решении которых учащиеся осуществляют полный перебор. 1. У Саши имеется 3 видеокассеты с мультфильмами и 2 кассеты с фильмами про Гарри Поттера. Сколькими способами он может выбрать одну кассету для просмотра? 2. У Миши есть 3 новые книжки и 2 автомобиля: «Джип» и «Мерседес». Сколькими способами он сможет составить подарок для Димы, состоящий из двух предметов? 3. У куклы Барби имеется 3 различных бальных платья и 2 шляпки: с вуалью и с перьями. Сколькими способами можно составить наряд для Барби? Приведем примеры задач, при решении которых учащиеся осуществляют сокращенный перебор. 1. Запишите все двузначные числа, которые можно составить из цифр 3, 4, 5, 6 так, чтобы число десятков было больше числа единиц. 2. Имеется 4 фигуры: большой и маленький треугольники, большой и маленький круги. Сколько существует способов расположения этих фигур в ряд, если на первое место мы поставим большой треугольник и одинаковые по форме фигуры не будут стоять рядом? 3. Запишите все четные двузначные числа, которые можно составить из цифр 3, 4, 5, 6. Особенность задач, которые предлагаются для решения на 3 этапе, состоит в увеличении возможных вариантов перебора. Приведем примеры задач третьего этапа. 1. У Сережи 2 автомобиля: «Мерседес» и «Волга», 5 солдатиков и 3 пистолета. Он хочет выбрать из этих игрушек один автомобиль, одного солдатика и один пистолет. Сколькими способами он сможет это сделать? 2. Часть стены прямоугольной формы разделена на клетки и имеет в длину 8 клеток, а в ширину 6. Мастеру нужно выложить ее кафельными плитками, использовав 5 плиток квадратной формы (размером 2´2 клетки) и 7 плиток прямоугольной формы (размером 1´4 клетки). Можно ли это сделать? Сколько плиток каждого вида нужно взять, чтобы выполнить заказ? Нарисуйте на листе в клеточку, как можно разместить плитки. 3. Имеется 3 зеленых и 2 желтых гирлянды. Сколько различных комбинаций из них можно составить? 4. На острове «Ро–ко–ко» только 3 буквы: а, б, в. В словах они могут повторяться не более двух раз. Сколько различных слов имеют жители этого острова, если все их слова – трехбуквенные? (из учебника Петерсон Л.Г.) С увеличением возможных вариантов меняются средства организации этого перебора. При решении таких задач целесообразно использовать таблицы, графы и «дерево возможностей», позволяющие упросить решение задачи. Так, графы позволяют расчленить ход рассуждений, четко провести перебор, не упустив никаких вариантов. Решение задач с использованием графов является основным содержанием третьего этапа в обучении младших школьников решению комбинаторных задач. При обучении решению задач с помощью графов также выделяются несколько этапов: На подготовительном этапе формируются умения заменять конкретный предмет его моделью, умения символически изображать связи между объектами задачи. Это период учащиеся переводят условие задачи на язык графических символов. Для этого учителю необходимо уметь ввести условное обозначение объектов и связей между ними; построить графическую модель, отражающую все данные задачи. Эти умения формируются при решении задач, включенных в курс математики, по которому обучаются школьники, по программе «Школа России». На следующем этапе решаются задачи с небольшим числом объектов и связей между ними. На втором этапе происходит дальнейшее обучение младших школьников решению задач с помощью графов. Характерной особенностью второго этапа обучения является постепенное увеличение количества рассматриваемых объектов; увеличение количества связей между объектами; необходимость использования для решения задач более одного вида графов. Так, в учебниках математики под редакцией Л.Г.Петерсон младших школьников знакомят с применением граф-дерева для решения комбинаторных задач. Вначале учат младших школьников понимать «язык» графов. Для этой цели учащимся могут быть предложены следующие задания: Задача 1. Нарисуйте домики, которые «зашифрованы», для этого пройдите по всем возможным путям от верхней точки до нижних (Рис.10).
2) Какое число зашифровано в выделенном пути? Покажите путь, в котором зашифровано число 5717 (Рис.11).
Затем учащиеся используют графы при решении комбинаторных задач. Для этой цели решают задания следующего вида. Задача. Из цифр 5, 8, 4, 0 составьте все возможные трехзначные числа, в которых нет одинаковых цифр. Сколько среди них чисел, меньших 800? Решение. Если числа, меньше 800, то первой цифрой в числе может быть либо 5, либо 4. Ставим две точки (Рис.12), и составим сначала все числа с цифрой 5, при этом второй цифрой может быть либо 8, либо 4, либо 0. Если первая цифра 5, вторая 8, то третьей могут быть либо 4, либо 0 и т.д. Этот граф помогает проводить перебор в определенной системе и не упускать какие-либо возможности.
Задача. Несколько приятелей при встрече пожали друг другу руки. Сколько встретилось приятелей, если рукопожатий было 10? Решение. Выясняется, что решить эту задачу, как предыдущие, не удается, так как неизвестно, сколько поставить точек, зато известно количество рукопожатий, то есть количество отрезков или ребер графа. Поэтому в данной ситуации можно предложить ученикам рассмотреть последовательно варианты: – если приятелей было двое (то получается одно рукопожатие, а это не соответствует условию задачи); – если приятелей было трое (то рукопожатий было 3); – если приятелей было четверо (рукопожатий − 6); – если приятелей было пятеро, то получается 10 рукопожатий. Получается, что если рукопожатий было 10, то встретилось 5 приятелей (рис.13). Возможно, учащиеся сами предложат начать с четырех точек, так как такой граф они уже чертили в задании 1, а он имеет 6 ребер. В этом случае число переборов будет меньше.
Задача. Сколько существует трехзначных чисел, в записи которых использованы только цифры 1, 4, 0? Требуемый граф изображен на рисунке 14.
Каждая ветвь этого дерева изображает одно из данных чисел. Кроме того, можно заметить, что количество чисел можно найти как произведение 2×3×3. Применение графов позволяет упростить решение комбинаторных задач, сделать ход рассуждений наглядным. Приведем примеры задач, решаемые с помощью графов, которые могут быть предложены учащимся. 1. Маша, Катя, Ира и Марина вечером по телефону созваниваются друг с другом. Сколько звонков было сделано, если каждая подружка поговорила по одному разу? 2. В турнире по шашкам участвовало 6 человек. Каждый с каждым сыграл по одной партии. Сколько партий они сыграли? 3. В розыгрыше первенства по футболу участвуют 15 команд. Каждая команда с каждой из остальных должна сыграть 2 раза: на своем и на чужом поле. Сколько матчей будет проведено в турнире? С нашей точки зрения, приведенные выше задачи, можно использовать на уроках математики. Решая такие задачи, у учащихся будет развиваться комбинаторный стиль мышления. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 325. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

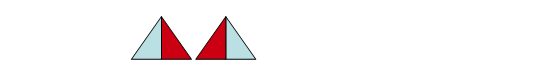 целесообразно задать наводящий вопрос: «Есть ли в задаче указание на то, что обязательно каждый парус надо закрасить двумя красками? Тогда как еще по-другому можно закрасить оставшиеся паруса?»
целесообразно задать наводящий вопрос: «Есть ли в задаче указание на то, что обязательно каждый парус надо закрасить двумя красками? Тогда как еще по-другому можно закрасить оставшиеся паруса?»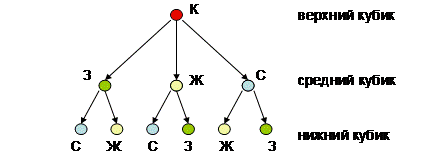 Рис.10
Рис.10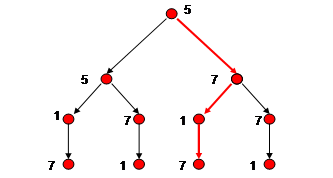 Рис.11
Рис.11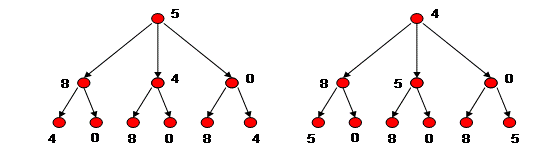 Рис.12
Рис.12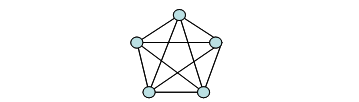 Рис.13
Рис.13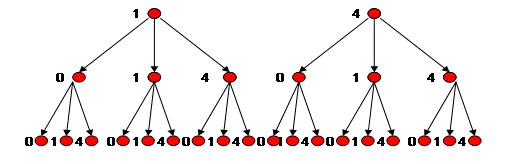 Рис.14
Рис.14