
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Пример содержания отчета по лабораторной работе №9 «Решение многокритериальной задачи»
1. Исходные данные:
Предприятие выпускает восемь видов товаров. Для производства указанных товаров используется 15 видов ресурсов. Рассматривалась проблема недостаточности дохода предприятия. Требуется определить программу производства товаров различного вида, обеспечивающую максимум среднего дохода предприятия. Параметры задачи представлены теми же числовыми данными, которые использовались при выполнении работы №2. Сформулированы дополнительные цели и критерии для решения задачи. Так, первой целью остается достижение максимального дохода. В качестве второй и третьей цели рассматривается максимизация использования ресурсов 5 и 8. Стремление к максимизации расхода указанных ресурсов оправданно, поскольку из имеющегося количества ресурса 5, составляющего 320 единиц, используется 31,7 единиц, а для ресурса 8 из 490 единиц используется 9,1 единиц.
2. Решение:
Первоначально была решена задача оптимизации по каждому локальному критерию. Решение по критерию 1 (максимизация дохода) представлено в таблице П25, а расход ресурсов в таблице П26:
Таблица П25. Оптимальный выпуск продукции по критерию 1
| Товары
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Доход
| | Количество (шт.)
| 13,93127
| 3,200906
| 0
| 5,386733
| 0,599527
| 0
| 20,1504
| 0
| | Цена (руб.)
| 25
| 23
| 10
| 22
| 18
| 19
| 24
| 20
| 1034,812
| Таблица П26. Расход ресурсов на выпуск продукции по критерию 1
| Ресурсы
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Расход ресурса
| Знак нера-венства
| Наличие
| | Ресурс 1 (ед. измерения)
| 2
| 4
| 3
| 5
| 3
| 1
| 4
| 3
| 150
| <=
| 150
| | Ресурс 2 (ед. измерения)
| 0,5
| 0,7
| 0
| 0,8
| 0,3
| 0
| 0
| 0,6
| 13,69
| <=
| 65
| | Ресурс 3 (ед. измерения)
| 12
| 24
| 30
| 0
| 0
| 10
| 15
| 22
| 546,25
| <=
| 650
| | Ресурс 4 (ед. измерения)
| 5
| 7
| 9
| 1
| 3
| 4
| 5
| 2
| 200
| <=
| 200
| | Ресурс 5 (ед. измерения)
| 0
| 0
| 0
| 5
| 8
| 5
| 0
| 0
| 31,73
| <=
| 320
| | Ресурс 6 (ед. измерения)
| 20
| 18
| 22
| 18
| 23
| 21
| 20
| 17
| 850
| <=
| 850
| | Ресурс 7 (ед. измерения)
| 9
| 6
| 8
| 4
| 7
| 8
| 9
| 5
| 351,68
| <=
| 600
| | Ресурс 8 (ед. измерения))
| 0
| 0,6
| 0,9
| 0,5
| 0,8
| 0,4
| 0,2
| 0,7
| 9,12
| <=
| 490
| | Ресурс 9 (ед. измерения)
| 8
| 9
| 7
| 8
| 7
| 8
| 9
| 9
| 368,90
| <=
| 700
| | Ресурс 10 (ед. измерения)
| 12
| 15
| 11
| 14
| 13
| 15
| 16
| 11
| 620,80
| <=
| 750
| | Ресурс 11 (ед. измерения)
| 0,22
| 0,35
| 0,45
| 0,12
| 0,05
| 0,19
| 0,25
| 0,36
| 9,90
| <=
| 220
| | Ресурс 12 (ед. измерения)
| 54
| 23
| 48
| 39
| 27
| 31
| 52
| 48
| 2100
| <=
| 2100
| | Ресурс 13 (ед. измерения)
| 13
| 18
| 19
| 15
| 12
| 14
| 17
| 16
| 669,27
| <=
| 1000
| | Ресурс 14 (ед. измерения)
| 2
| 4
| 2
| 1
| 5
| 7
| 1
| 3
| 69,20
| <=
| 450
| | Ресурс 15 (ед. измерения)
| 27
| 25
| 20
| 24
| 18
| 24
| 25
| 22
| 1100
| <=
| 1100
| Расчеты по критерию 2 представлены в таблицах П27 и П28:
Таблица П27. Оптимальный выпуск продукции по критерию 2
| Товары
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Доход
| | Количество (шт.)
| 0,00
| 0,00
| 0
| 0,00
| 36,96
| 0
| 0,00
| 0
| | Цена (руб.)
| 25
| 23
| 10
| 22
| 18
| 19
| 24
| 20
| 665,2174
| Таблица П28. Расход ресурсов на выпуск продукции по критерию 2
| Ресурсы
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Расход ресурса
| Знак нера-венства
| Наличие
| | Ресурс 1 (ед. измерения)
| 2
| 4
| 3
| 5
| 3
| 1
| 4
| 3
| 110,8696
| <=
| 150
| | Ресурс 2 (ед. измерения)
| 0,5
| 0,7
| 0
| 0,8
| 0,3
| 0
| 0
| 0,6
| 11,09
| <=
| 65
| | Ресурс 3 (ед. измерения)
| 12
| 24
| 30
| 0
| 0
| 10
| 15
| 22
| 0,00
| <=
| 650
| | Ресурс 4 (ед. измерения)
| 5
| 7
| 9
| 1
| 3
| 4
| 5
| 2
| 110,8696
| <=
| 200
| | Ресурс 5 (ед. измерения)
| 0
| 0
| 0
| 5
| 8
| 5
| 0
| 0
| 295,65
| <=
| 320
| | Ресурс 6 (ед. измерения)
| 20
| 18
| 22
| 18
| 23
| 21
| 20
| 17
| 850
| <=
| 850
| | Ресурс 7 (ед. измерения)
| 9
| 6
| 8
| 4
| 7
| 8
| 9
| 5
| 258,70
| <=
| 600
| | Ресурс 8 (ед. измерения))
| 0
| 0,6
| 0,9
| 0,5
| 0,8
| 0,4
| 0,2
| 0,7
| 29,57
| <=
| 490
| | Ресурс 9 (ед. измерения)
| 8
| 9
| 7
| 8
| 7
| 8
| 9
| 9
| 258,70
| <=
| 700
| | Ресурс 10 (ед. измерения)
| 12
| 15
| 11
| 14
| 13
| 15
| 16
| 11
| 480,43
| <=
| 750
| | Ресурс 11 (ед. измерения)
| 0,22
| 0,35
| 0,45
| 0,12
| 0,05
| 0,19
| 0,25
| 0,36
| 1,85
| <=
| 220
| | Ресурс 12 (ед. измерения)
| 54
| 23
| 48
| 39
| 27
| 31
| 52
| 48
| 997,8261
| <=
| 2100
| | Ресурс 13 (ед. измерения)
| 13
| 18
| 19
| 15
| 12
| 14
| 17
| 16
| 443,48
| <=
| 1000
| | Ресурс 14 (ед. измерения)
| 2
| 4
| 2
| 1
| 5
| 7
| 1
| 3
| 184,78
| <=
| 450
| | Ресурс 15 (ед. измерения)
| 27
| 25
| 20
| 24
| 18
| 24
| 25
| 22
| 665,2174
| <=
| 1100
| Расчеты по критерию 3 представлены в таблицах П29 и П30:
Таблица П29. Оптимальный выпуск продукции по критерию 3
| Товары
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Доход
| | Количество (шт.)
| 0,00
| 0,00
| 0
| 0,00
| 15,12
| 0
| 0,00
| 29,54545
| | Цена (руб.)
| 25
| 23
| 10
| 22
| 18
| 19
| 24
| 20
| 863,0435
| Таблица П30. Расход ресурсов на выпуск продукции по критерию 3
| Ресурсы
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Расход ресурса
| Знак нера-венства
| Наличие
| | Ресурс 1 (ед. измерения)
| 2
| 4
| 3
| 5
| 3
| 1
| 4
| 3
| 133,9921
| <=
| 150
| | Ресурс 2 (ед. измерения)
| 0,5
| 0,7
| 0
| 0,8
| 0,3
| 0
| 0
| 0,6
| 22,26
| <=
| 65
| | Ресурс 3 (ед. измерения)
| 12
| 24
| 30
| 0
| 0
| 10
| 15
| 22
| 650,00
| <=
| 650
| | Ресурс 4 (ед. измерения)
| 5
| 7
| 9
| 1
| 3
| 4
| 5
| 2
| 104,4466
| <=
| 200
| | Ресурс 5 (ед. измерения)
| 0
| 0
| 0
| 5
| 8
| 5
| 0
| 0
| 120,95
| <=
| 320
| | Ресурс 6 (ед. измерения)
| 20
| 18
| 22
| 18
| 23
| 21
| 20
| 17
| 850
| <=
| 850
| | Ресурс 7 (ед. измерения)
| 9
| 6
| 8
| 4
| 7
| 8
| 9
| 5
| 253,56
| <=
| 600
| | Ресурс 8 (ед. измерения))
| 0
| 0,6
| 0,9
| 0,5
| 0,8
| 0,4
| 0,2
| 0,7
| 32,78
| <=
| 490
| | Ресурс 9 (ед. измерения)
| 8
| 9
| 7
| 8
| 7
| 8
| 9
| 9
| 371,74
| <=
| 700
| | Ресурс 10 (ед. измерения)
| 12
| 15
| 11
| 14
| 13
| 15
| 16
| 11
| 521,54
| <=
| 750
| | Ресурс 11 (ед. измерения)
| 0,22
| 0,35
| 0,45
| 0,12
| 0,05
| 0,19
| 0,25
| 0,36
| 11,39
| <=
| 220
| | Ресурс 12 (ед. измерения)
| 54
| 23
| 48
| 39
| 27
| 31
| 52
| 48
| 1826,383
| <=
| 2100
| | Ресурс 13 (ед. измерения)
| 13
| 18
| 19
| 15
| 12
| 14
| 17
| 16
| 654,15
| <=
| 1000
| | Ресурс 14 (ед. измерения)
| 2
| 4
| 2
| 1
| 5
| 7
| 1
| 3
| 164,23
| <=
| 450
| | Ресурс 15 (ед. измерения)
| 27
| 25
| 20
| 24
| 18
| 24
| 25
| 22
| 922,1344
| <=
| 1100
| Очевидно, что оптимальное решение по одному критерию не совпадает с оптимальным решением по другим, т.е. критерии противоречивы. Задались вектором важности критериев  и решили задачу методом скаляризации векторного критерия воспользовавшись формулой: и решили задачу методом скаляризации векторного критерия воспользовавшись формулой:
 . .
Оптимальное решение при выбранной схеме компромисса и заданных значениях вектора важности имеет вид {21,18; 0; 0; 19,61; 3,19; 0; 0; 0}, а
 . .
Значения локальных критериев равны соответственно  , , 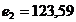 , ,  . .
При другом векторе важности 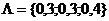 : :
 . .
При этом  ; ; 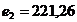 ; ; 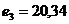 , а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}. , а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}.
Воспользовались методом квазиравенства, при реализации которого добиваются обеспечения разности между величинами локальных критериев, не превышающих некоторой заданной величины  . Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда . Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда
 , ,  . .
Пусть 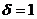 . Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения . Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения  , , 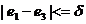 , , 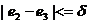 записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32: записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32:
Таблица П31. Оптимальный выпуск продукции по принципу квазиравенства
| Товары
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Доход 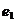
| Критерий 2 
| Критерий 3 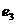
| | Количество (шт.)
| 0
| 0
| 0,088889
| 0
| 0,011111
| 0
| 0
| 0
| | Цена (руб.)
| 25
| 23
| 10
| 22
| 18
| 19
| 24
| 20
| 1,088888846
| 0,088889
| 0,088889
| Таблица П32. Расход ресурсов на выпуск продукции по принципу квазиравенства
| Ресурсы
| Товар 1
| Товар 2
| Товар 3
| Товар 4
| Товар 5
| Товар 6
| Товар 7
| Товар 8
| Расход ресурса
| Знак нера-венства
| Наличие
| | Ресурс 1 (ед. измерения)
| 2
| 4
| 3
| 5
| 3
| 1
| 4
| 3
| 0,3
| <=
| 150
| | Ресурс 2 (ед. измерения)
| 0,5
| 0,7
| 0
| 0,8
| 0,3
| 0
| 0
| 0,6
| 0,003333332
| <=
| 65
| | Ресурс 3 (ед. измерения)
| 12
| 24
| 30
| 0
| 0
| 10
| 15
| 22
| 2,666666826
| <=
| 650
| | Ресурс 4 (ед. измерения)
| 5
| 7
| 9
| 1
| 3
| 4
| 5
| 2
| 0,833333365
| <=
| 200
| | Ресурс 5 (ед. измерения)
| 0
| 0
| 0
| 5
| 8
| 5
| 0
| 0
| 0,088888846
| <=
| 320
| | Ресурс 6 (ед. измерения)
| 20
| 18
| 22
| 18
| 23
| 21
| 20
| 17
| 2,211111106
| <=
| 850
| | Ресурс 7 (ед. измерения)
| 9
| 6
| 8
| 4
| 7
| 8
| 9
| 5
| 0,788888894
| <=
| 600
| | Ресурс 8 (ед. измерения))
| 0
| 0,6
| 0,9
| 0,5
| 0,8
| 0,4
| 0,2
| 0,7
| 0,088888889
| <=
| 490
| | Ресурс 9 (ед. измерения)
| 8
| 9
| 7
| 8
| 7
| 8
| 9
| 9
| 0,7
| <=
| 700
| | Ресурс 10 (ед. измерения)
| 12
| 15
| 11
| 14
| 13
| 15
| 16
| 11
| 1,122222212
| <=
| 750
| | Ресурс 11 (ед. измерения)
| 0,22
| 0,35
| 0,45
| 0,12
| 0,05
| 0,19
| 0,25
| 0,36
| 0,040555558
| <=
| 220
| | Ресурс 12 (ед. измерения)
| 54
| 23
| 48
| 39
| 27
| 31
| 52
| 48
| 4,566666778
| <=
| 2100
| | Ресурс 13 (ед. измерения)
| 13
| 18
| 19
| 15
| 12
| 14
| 17
| 16
| 1,822222259
| <=
| 1000
| | Ресурс 14 (ед. измерения)
| 2
| 4
| 2
| 1
| 5
| 7
| 1
| 3
| 0,233333317
| <=
| 450
| | Ресурс 15 (ед. измерения)
| 27
| 25
| 20
| 24
| 18
| 24
| 25
| 22
| 1,977777788
| <=
| 1100
| 
|
|
|
|
|
|
|
|
| 1
|
| 1
| 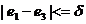
|
|
|
|
|
|
|
|
| 0,999999957
|
| 0,999999957
| 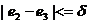
|
|
|
|
|
|
|
|
| 4,29969E-08
|
| 4,29969E-08
| Решение задачи оптимизации по принципу максимина совпадает с решением при максимизации локального критерия 3 (таблица П29), поскольку он во всех трех случаях имеет минимальное значение.
Принцип абсолютной уступки соответствует критерию:
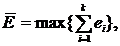
В нашем случае составляет  , при этом , при этом 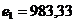 , ,  , ,  . Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}. . Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}.
Компромисс по принципу последовательной уступки. Предположили, что критерии ранжированы по важности в соответствии с их номерами. Нашли оптимальное решение по критерию 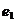 . Назначили уступку . Назначили уступку  , которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия , которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия 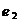 . Тогда . Тогда  , а , а 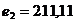 . Ввели уступку по второму критерию . Ввели уступку по второму критерию 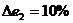 и максимизировали значение показателя и максимизировали значение показателя 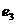 . Тогда . Тогда  ; ;  , а , а  . Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}. . Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}.
3. Выводы:
Результаты решения многокритериальной задачи, полученные с помощью различных методов выбора компромисса, сведены в таблицу П33.
Таблица П33. Результаты решения многокритериальной задачи на основе различных принципов выбора компромисса
|


 и решили задачу методом скаляризации векторного критерия воспользовавшись формулой:
и решили задачу методом скаляризации векторного критерия воспользовавшись формулой: .
. .
. ,
, 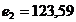 ,
,  .
.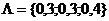 :
: .
. ;
; 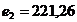 ;
; 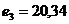 , а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}.
, а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}. . Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда
. Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда ,
,  .
.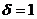 . Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения
. Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения  ,
, 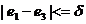 ,
, 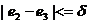 записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32:
записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32: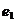

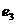
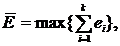
 , при этом
, при этом 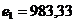 ,
,  ,
,  . Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}.
. Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}. , которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия
, которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия 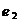 . Тогда
. Тогда  , а
, а 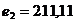 . Ввели уступку по второму критерию
. Ввели уступку по второму критерию 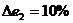 и максимизировали значение показателя
и максимизировали значение показателя  , а
, а  . Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}.
. Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}.