
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства условного математического ожидания. ⇐ ПредыдущаяСтр 3 из 3 1. M(C½h) = C 2. M(ax + b½h) = aM(x½h) + b 3. M(x + h½n) = M(x½n) + M(h½n) 4. M(xh½n) = M(x½n)M(h½n),еслиxиhнезависимыпри условии ν. 5. M[ M(x½h)]=Mx
6.
7.M(x/h) = Mx, если x и h - независимы. 8.
Функцию M(x /h) называют функцией регрессииили просто регрессией с. величины xна с. величину h. График функции M(x /h)называют линией регрессии с. величины xна с. величину h. Линий регрессии две M(x /h) и M(h /x). В общем случае они между собой не совпадают. M(x/h)
Билет 23 1.Формула полной вероятности
Формула справедлива для счетного набора гипотез 2. Дискретные случайные величины определение, ряд распределения, функция распределения, примеры. Пуассоновское распределение: его параметры с применением производящей функции Случайная величина  Если при описании случайной величины
Постоянная величина С. Она принимает единственное значение с вероятностью, равной единице. Индикатор события А.
Cлучайная величина
Производящей функцией для дискретно распределенной с. величины ξ называется функция 1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин. 2. 3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.
3.Условное распределение для двух непрерывных св. Условные функции распределения и плотности распределения.
Как показано в [7] такой предел всегда существует, но в определенном смысле: он является производной Радона-Никодима одной меры относительно другой. Поскольку событие
Так как:
Следовательно,
Функция
С использованием свойства 4 плотностей распределения и опустив в левой части у функции
Аналогичным рассуждением может быть получена формула:
Формулу (3.16) можно переписать в виде:
которая напоминает формулу умножения вероятностей для случайных событий
Билет 24 1. Аксиоматическое определение вероятности. Аксиомы непрерывности. Задано измеримое пространство (Ω, F). Ω – пространство э. событий, F – некоторая σ-алгебра событий (множества из F считаются событиями и только они). Вероятностью событияА из σ-алгебры F называется вещественная функция, определенная на F и удовлетворяющая следующим свойствам (аксиомам): А1. А2. А3. Если последовательность событий Вероятность, заданную на σ-алгебре F, называют вероятностной мерой. А3’: если события А4: Пусть последовательность событий А4’: пусть последовательность событий 2Пуассоновское распределение: его параметры с применением производящей функции Cлучайная величина
Производящей функцией для дискретно распределенной с. величины ξ называется функция 1. Если производящие функции двух с. величин совпадают, то совпадают и распределения этих с. величин. 2. 3. Если ξ и η – независимые с. величины, то производящая функция произведения этих с. величин равна произведению производящих функций сомножителей.
3.Совместная функция распределения, основные свойства.
все Основной характеристикой случайного вектора 1. 2. 3. 4. 5. 6. 7. Эту формулу можно вывести, исходя из представления события
|
||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 183. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 , формула полного математического ожидания.
, формула полного математического ожидания. , hи j – некоторые функции
, hи j – некоторые функции
 .
.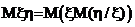


 На плоскости (y,х) уравнение этой прямой имеет вид х=a+by. M(h/x)= с+ dx, гдес=
На плоскости (y,х) уравнение этой прямой имеет вид х=a+by. M(h/x)= с+ dx, гдес=  ,
, ,
,  для регрессии η на ξ и регрессии
для регрессии η на ξ и регрессии  на η соответственно. Прямые регрессии проходят через центр рассеивания – точку (
на η соответственно. Прямые регрессии проходят через центр рассеивания – точку (  ) с угловым коэффициентом
) с угловым коэффициентом  . Так как |ρ| ≤1, то |
. Так как |ρ| ≤1, то | 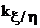 | ≥ |
| ≥ |  |, что означает, что прямая регрессии
|, что означает, что прямая регрессии  всегда расположена более круто по отношению к оси Ох, чем вторая регрессия. При |ρ| =1 они совпадают, при ρ =0 прямые распадаются на две прямые, параллельные осям координат – вырожденный случай регрессии.
всегда расположена более круто по отношению к оси Ох, чем вторая регрессия. При |ρ| =1 они совпадают, при ρ =0 прямые распадаются на две прямые, параллельные осям координат – вырожденный случай регрессии.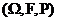 - вероятностное пространство и события
- вероятностное пространство и события 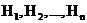 образуют в нем полную группу событий:1)
образуют в нем полную группу событий:1)  ; 2)
; 2)  ; 3)
; 3)  . События
. События 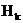 часто при этом называют гипотезами.
часто при этом называют гипотезами. , из условия
, из условия 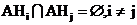 .
.  .
. 
 , причём вероятность события
, причём вероятность события  Набор вероятностей
Набор вероятностей  называют рядом распределения с. величины.
называют рядом распределения с. величины.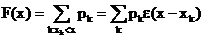 , где
, где  , если
, если  и
и 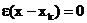 , если
, если  .
.

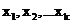 .
.  , то
, то  , где множества
, где множества 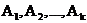 образуют разбиение пространства
образуют разбиение пространства  – они попарно не пересекаются и их сумма равна
– они попарно не пересекаются и их сумма равна  имеет вид:
имеет вид:



 - параметр распределения Пуассона.
- параметр распределения Пуассона.
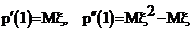 .
.
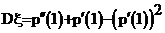 Действительно,
Действительно,  . Далее,
. Далее, 


 .
.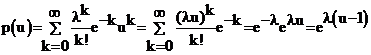 ,
, 
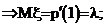
 .
. и назовем условной функцией распределения
и назовем условной функцией распределения  предел этой условной вероятности при
предел этой условной вероятности при  :
: (3.12)
(3.12) есть объединение непересекающихся событий
есть объединение непересекающихся событий  и
и  , тогда
, тогда 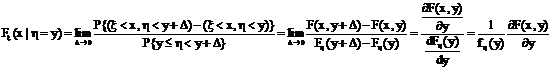 Итак,
Итак, (3.13)
(3.13) (3.14)
(3.14) (3.15)
(3.15) имеет производную по x , т.е. существует условная плотность распределения случайной величины
имеет производную по x , т.е. существует условная плотность распределения случайной величины 
 (3.16)
(3.16)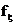 индекс
индекс  (3.17)
(3.17) (3.18)
(3.18)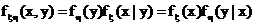 (3.19)
(3.19)
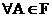 - аксиома неотрицательности;
- аксиома неотрицательности; - аксиома нормированности;
- аксиома нормированности;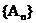 такова, что
такова, что  то
то  - аддитивность сложения.
- аддитивность сложения. несовместны, то
несовместны, то  ;
; такова, что
такова, что  ,
,  , и
, и  .Тогда
.Тогда  - аксиома непрерывности.
- аксиома непрерывности.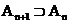 ,
,  . Тогда
. Тогда  .
.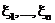 - случайные величины, заданные на нем. Каждому значению
- случайные величины, заданные на нем. Каждому значению  они ставят в соответствие вектор
они ставят в соответствие вектор  .Отображение
.Отображение  , задаваемое совокупностью случайных величин
, задаваемое совокупностью случайных величин  , называется случайным вектором
, называется случайным вектором , измеримые функции, случайным вектором
, измеримые функции, случайным вектором  , где
, где 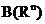 – борелевская
– борелевская 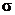 -алгебра в
-алгебра в  . Необходимым и достаточным условием измеримости случайного вектора
. Необходимым и достаточным условием измеримости случайного вектора 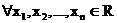
 .
. .
.
 ;
;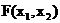 - неубывающая функция по каждому из своих аргументов;
- неубывающая функция по каждому из своих аргументов; ;
; ;
; ;
;  ;
;  ;
; .
. в виде алгебраической суммы событий:
в виде алгебраической суммы событий: 
 .
.