Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обобщенное уравнение состояния ⇐ ПредыдущаяСтр 3 из 3 Обобщенное уравнение состояния для схемы произвольной конфигурации имеет вид
Матричная форма записи уравнения, где Уравнение (1) объединяет два матричных уравнения. Уравнение по первому закону Кирхгофа
Уравнение по второму закону Кирхгофа
где
а вектор–столбцы
Для формирования обобщенного уравнения состояния (1) необходимо предварительно определить матрицы инциденций
При известных токах в ветвях можно определить напряжения в узлах. Для этого сначала по закону Ома определяем падение напряжения в ветвях схемы 
Затем из уравнения Покажем применение описанной методики на примере решения следующих задач. При расчетах режимов электрических сетей могут иметь место два случая: · схема замещения электрической сети не содержит замкнутых контуров, · схема замещения электрической сети содержит замкнутые контуры. Первая из рассмотренных ниже задач посвящена расчету установившегося режима электрической сети, не содержащей замкнутых контуров, вторая расчету установившегося режима для сетей, содержащих замкнутые контуры. Пример.
Рис. 2 Для схемы, представленной на рис.2 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки узлов равны Матрица задающих токов принимает вид
Матрица задающих токов равна матрице токов нагрузок, взятой с противоположным знаком. Выберем в качестве балансирующего узла
Из обобщенного уравнения состояния
Расчетная часть Дано:
Создадим вектор-столбец токов:
Обобщенное уравнение состояния :
Вычисление обратной матрицы М классическим методом:
Транспонируем:
Находим значения элементов путем вычеркивания строки и столбца:
Вписываем полученные значения в их точки:
Найдем определитель:
Разделим на определитель и получим обратную матрицу:
Теперь найдем обратную матрицу в системе MATLAB:
Вычисление токов в ветвях в системе MATLAB:
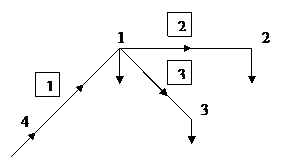
Пример. Для схемы представленной на рис.3 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. Токи нагрузки равны
Рис. 3 В начале составим первую и вторую матрицы инциденций (
Столбцы в этой матрицы можно условно пронумеровать как связи Первая матрица инциденций без балансирующего узла будет иметь вид:
В нашей схеме замещения всего один независимый контур, в соответствии с этим вторая матрица инциденций примет вид:
Столбцы в этой матрице имеет ту же нумерацию, что и в первой матрице инциденций. Запишем для нашей схемы обобщенное уравнение состояния
Последний элемент в вектор- столбце Найденные токи принимают значения
По закону Ома определим падение напряжения на ветвях схемы
Используя уравнение
Перемножая матрицы в матричном уравнении, получаем
Расчетная часть Дано:
Первая матрица инциденции:
Принимаем в качестве балансирующего узла узел 4 исключаем его:
Вторая матрица инциденции:
Составим матрицу сопротивлений:
|
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 238. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
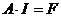 (1)
(1)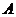 матрица параметров схемы замещения, где
матрица параметров схемы замещения, где 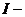 вектор- столбец токов в ветвях,
вектор- столбец токов в ветвях,  - число ветвей в схеме замещения,
- число ветвей в схеме замещения, 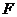 - вектор- столбец исходных параметров режима.
- вектор- столбец исходных параметров режима.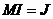 .
. 
 ,
,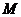 матрица размерностью
матрица размерностью 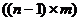 матрица соединений ветвей в узлах ( без балансирующего узла), здесь
матрица соединений ветвей в узлах ( без балансирующего узла), здесь  - число узлов схемы замещения,
- число узлов схемы замещения, 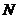 - матрица размерностью
- матрица размерностью  , матрица соединений ветвей в независимые контуры,
, матрица соединений ветвей в независимые контуры, 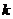 - число независимых контуров.
- число независимых контуров.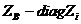 диагональная матрица сопротивлений ветвей.
диагональная матрица сопротивлений ветвей.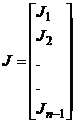 - вектор-столбец задающих токов в узлах.
- вектор-столбец задающих токов в узлах. - вектор-столбец контурных ЭДС ветвей, входящих в каждый независимый контур. Матрицы
- вектор-столбец контурных ЭДС ветвей, входящих в каждый независимый контур. Матрицы 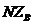 можно рассматривать как блоки одной объединенной матрицы параметров схемы замещения
можно рассматривать как блоки одной объединенной матрицы параметров схемы замещения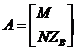 ,
, и
и 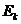 как блоки одной объединенной матрицы исходных параметров режима
как блоки одной объединенной матрицы исходных параметров режима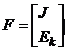 .
.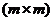 . Тогда из уравнения (1) используя метод обратной матрицы можно сразу определить токи в ветвях
. Тогда из уравнения (1) используя метод обратной матрицы можно сразу определить токи в ветвях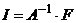
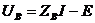 .
.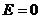 , то закон Ома принимает вид
, то закон Ома принимает вид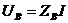
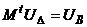 определяем напряжения в узлах схемы замещения. Здесь матрица
определяем напряжения в узлах схемы замещения. Здесь матрица 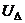 представляет собой напряжения узлов относительно базисного
представляет собой напряжения узлов относительно базисного 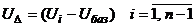 .
.
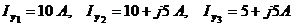 .
.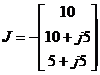
 узел. Обозначим через
узел. Обозначим через 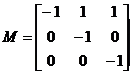
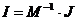
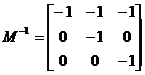
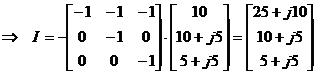

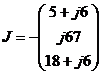
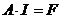
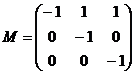
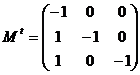
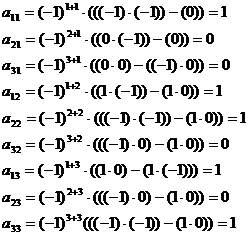

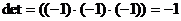
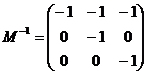

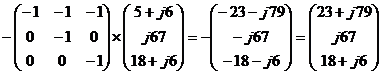

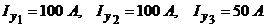 . Узел
. Узел 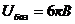 . Сопротивления ветвей схемы соответственно равны
. Сопротивления ветвей схемы соответственно равны  .
.
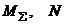 ) для нашего графа.
) для нашего графа. , узел
, узел 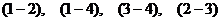 . Связи однозначно определяют направление ветвей в схеме замещения, так например, связь
. Связи однозначно определяют направление ветвей в схеме замещения, так например, связь 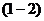 означает что данная ветвь имеет направление из узла
означает что данная ветвь имеет направление из узла 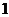 в узел
в узел 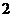 .
.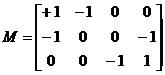 .
.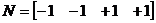 .
.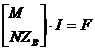
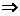
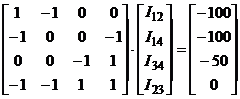 .
.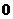 , т.к. ЭДС в ветвях отсутствует. Данная система может быть решена относительно искомых токов в ветвях любым методом решения систем линейных алгебраических уравнений (например, методом обратной матрицы или методом Гаусса).
, т.к. ЭДС в ветвях отсутствует. Данная система может быть решена относительно искомых токов в ветвях любым методом решения систем линейных алгебраических уравнений (например, методом обратной матрицы или методом Гаусса).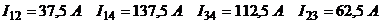 .
.
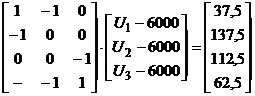 .
. неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким-либо методом решения систем линейных алгебраических уравнений. В результате получаем
неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким-либо методом решения систем линейных алгебраических уравнений. В результате получаем 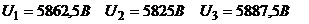 .
.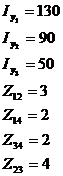

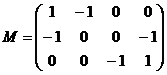 Первая матрица инциденции
Первая матрица инциденции