
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение эмпирической функции распределенияСтр 1 из 3Следующая ⇒ ЭЛЕМЕНТЫ ТЕОРИИ Из продукции одного токарно-револьверного автомата, обрабатывающего ролики d = 20 мм, взята выборка объемом 100 шт. Ролики измерены по диаметру микрометром с ценой деления 0,01 мм и результаты измерений приведены ниже.
Рассматриваемая нами случайная величина Х может принять любое значение из некоторого интервала, то есть является непрерывной случайной величиной. Решение вопросов математической статистики (установить закон распределения, определить параметры, проверить гипотезу) по данным выборки слагается из следующих пунктов: 1 Проверка случайности и независимости результатов наблюдений (проверка выборки на стохастичность). 2 Построение эмпирической функции распределения. 3 Вычисление точных оценок параметров распределения (выборочной средней, выборочной дисперсии, показателя асимметрии, показателя эксцесса). 4 Вычисление интервальных оценок. 5 Построение теоретической функции распределения. 6 Проверка гипотезы о виде распределения.  Проверка выборки на стохастичность Пред тем как подвергнуть результаты наблюдений соответствующей статистической обработке, необходимо убедиться, что они образуют случайную выборку. С этой целью воспользуемся критерием «восходящих» и «нисходящих» серий. В этом критерии исследуется последовательность знаков – плюсов и минусов. Исходным пунктом является выборка х1, х2, … хn (в приведенном примере значения признака). На i – ом месте этой выборки ставится плюс, если Хi+1 – Xi> 0, минус, если хi+1 – xi< 0.(Если хin= хi,то значение хiпропускается). В приведенном примере мы получим следующую последовательность знаков: +-+--+-+-+-+-+-+++-+--+-+--++++--+--+-+-+-+-+--+-+-++++-+-+-+-+++-+-++--+++---+++--++ Под «серией» будем понимать последовательность подряд идущих плюсов или минусов. В частности, «серия» может состоять только из одного плюса или одного минуса, тогда ее протяженность равна единице. Общее число, серий в выборке обозначим через n(n), протяженность самой длинной серии – t(n). Для нашего примера n =100; n(n) = 59; t(n) = 4. При уровне значимости a = 0,05 количественное выражение правила проверки на случайность следующее:
t(n) <t0(n), где t0(n) определяется из соотношений:
Если хотя бы одно из неравенств (1) не выполняется, то предположение о случайности выборки следует отвергнуть; так как 26 < n < 153, то t0(n) = 6>t(n), то есть второе неравенство выполняется. Проверим первое неравенство.
Так как выполнено и второе неравенство, то в приведенном примере выборка случайная. Построение эмпирической функции распределения При большом объеме выборки (порядка сотен) простая статистическая совокупность престает быть удобной формой записи статистического материала - она становится громоздкой и мало наглядной. Для придания большей компактности элементы выборки объединяют в группы (интервалы), число которых колеблется от 5 до 40, в зависимости от объема выборки. Гост II.006-74 по правилам согласия опытного распределения с теоретическим рекомендует следующее число интервалов К в зависимости от объема выборки n:
Некоторые авторы для определения числа интервалов рекомендуют пользоваться эмпирическими формулами:
Просматривая результаты испытаний, выбираем наибольшее и наименьшее наблюдаемые значения признака X(xmax, xmin) и находим величину размаха варьирования
Зная число интервалов и размах варьирования R, находим длину каждого интервала h по формуле
В рассмотренном примере: хmin= 19,80; xmax= 19,89; R = xmax– хmin= 0,09. Значение К =10 подсчитано по формуле Тогда h = 0,009. Чтобы значение признака попадало на границу интервала, длину интервала увеличивают до h = 0,011. Далее приступают к заполнению таблицы 1. В колонке 1 записаны полученные интервалы, расположенные в порядке возрастания значений признака. В колонке 2 отмечено наличие признака, попавшего в рассматриваемый интервал (для облечения подсчета количества значений признака их группируют по 5). Количество m (абсолютная частота признака) записывают в колонку 3. В колонке 4 записывают относительные частоты Таблица 1.
Данные таблицы 1 используют для графического изображения статистического ряда либо в виде гистограммы, либо в виде эмпирической функции распределения. Это графическое изображение позволяет представить в наглядной форме закономерности, присущие генеральной совокупности. Для построения гистограммы (рисунок 1) на оси абсцисс последовательно откладываются интервалы изменения значения признака. На этих отрезках, как на основании, строят прямоугольники с высотами, равными
Рисунок 1 – Гистограмма График эмпирической функции распределения (рисунок 2) строят в координатах (х, где x – значения признака;
Под значением признака понимают середины рассматриваемых интервалов, а под накопительной
Рисунок 2 – Вычисление точных оценок параметров распределения Статистический ряд – первый шаг к осмыслению ряда наблюдений. Однако на практике этого недостаточно. Статистические ряды, имеющие похожие графические изображения, могут различаться: 1. Эмпирической средней 2. Средним квадратическим отклонением S - рассеянием наблюдения вокруг эмпирической средней; 3. Показателем ассиметрии Аs, характеризующим скошенность гистограммы; 4. Показателем эксцесса Es, характеризующим островершинность гистограммы. Перечисленные числовые характеристики называют статистическими. По ним судят о характерных особенностях статистического ряда. Эти характеристики вычисляются по формулам:
где ximi – середина и абсолютная частота i - го интервала; k – число интервалов. Для удобства вычислений
Xa=19,84 Обозначим где h – длина интервала, и подставим в последнюю формулу
Для вычисления эмпирической дисперсии S2 используют формулу
Показатель асимметрии вычисляют по формуле
Показатель эксцесса находят по формуле:
Для удобства вычислений Таблица 2.
Подставляя данные таблицы 2 в формулы (3) – (6), находим:
Заметим что для нормального распределения As= Es=0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 594. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1)
 .
. или
или  .
. .
. .
. .
. значений признака.
значений признака. соответствующего интервала. Полученная ступенчатая фигура называется гистограммой.
соответствующего интервала. Полученная ступенчатая фигура называется гистограммой.
 ) либо (х,
) либо (х, 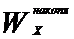 ),
), - накопленная абсолютная частота.
- накопленная абсолютная частота. частотой – сумму частот всех предшествующих и рассматриваемого интервалов.
частотой – сумму частот всех предшествующих и рассматриваемого интервалов.

 – значением признака, вокруг которого группируются наблюдения;
– значением признака, вокруг которого группируются наблюдения; , (2)
, (2) , S, As, Es иногда используют метод ложного нуля, которым и воспользуемся. Для этого выбираем значения ха, около которого наиболее часто встречается значение признака, тогда
, S, As, Es иногда используют метод ложного нуля, которым и воспользуемся. Для этого выбираем значения ха, около которого наиболее часто встречается значение признака, тогда .
. ,
, (3)
(3) (4)
(4) (5)
(5) (6)
(6)