Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальное исчисление функций нескольких переменных ⇐ ПредыдущаяСтр 3 из 3 141. Дана функция 142. Дана функция 143. Дана функция 144. Дана функция 145.Дана функция 146. Дана функция 147. Дана функция 148. Дана функция 149. Дана функция 150. Дана функция
151-160. Дана функция
161. 162. 163. 164. 165. 166. 167. 168. 169. 170. 171-180.Найти наибольшее и наименьшее значения функции в замкнутой области 171. 172. 173. 174. 175. 176. 177. 178. 179. 180. 181-190.Даны: функция 181. 182. 183. 184. 185. 186. 187. 188. 189. 190. Неопределенный и определенный интегралы 191-200.Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием. 191.а) в) 192. а) в) 193. а) в) 194.а) в)  195.а) в) 196.а) в) 197.а) в) 198. а) в) 199. а) в) 200. а) в)
201.Вычислить площадь фигуры, ограниченной параболами 202. Вычислить площадь фигуры, ограниченной гиперболой 203.Вычислить площадь фигуры, ограниченной астроидой 204. Вычислить площадь фигуры, ограниченной астроидой 205. Вычислить объем тела, образованного вращением вокруг оси 206. Вычислить объем тела, образованного вращением вокруг оси 207.Вычислить объем тела, образованного вращением вокруг оси 208. Вычислить длину дуги, параболы 209.Вычислить длину одной арки циклоиды 200.Вычислить длину первого витка архимедовой спирали 201-210.Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах 201. 202. 203. 204. 205. 206. 207. 208. 209. 210. 211-220.Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость 211. 212. 213. 214. 215. 216. 217. 218. 219. 220.
Форма промежуточного контроля Экзамен Перечень примерных вопросов для подготовки к экзамену 1. Функции нескольких переменных. Область определения. Предел. Непрерывность. 2. Частные производные функции нескольких переменных. Частные производные высших порядков. 3. Производные сложной и неявно заданной функции нескольких переменных. 4. Частное и полное приращения функции нескольких переменных. Полный дифференциал. 5. Уравнения касательной плоскости и нормали к поверхности. 6. Экстремум функции нескольких переменных. 7. Неопределенный интеграл. Свойства. Таблица. 8. Основные методы интегрирования. 9. Интегрирование рациональных дробей. 10. Интегрирование иррациональных функций. 11. Интегрирование тригонометрических функций. 12. Определенный интеграл. 13. Несобственные интегралы.
Основная литература 1.Шипачев В.С. Высшая математика: Учеб.для вузов / В.С. Шипачев. – 6-е изд., стер. – М.: Высш. шк., 2003. – 479 с. 2.Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб.для втузов. В 2-х т. Т. I: – М.: Интеграл – Пресс, 2004. – 416 с. 3.Шипачев В.С. Задачник по высшей математике: Учеб.пособие для вузов / В.С. Шипачев. – 3-е изд., стер. – М.: Высш. шк., 2003. – 304 с. 4.Баврин И.И. Высшая математика: Учеб.для студ. естественнонаучных специальностей педагогических вузов. – 2-е изд., стер. – М.: Изд. центр «Академия»; Высш. шк., 2001. – 616 с. 5.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I: Учеб.пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1999. – 304 с.
Дополнительная литература 1.Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-пресс, 2004. 2.Лунгу К.Н., Письменный Д.Т. Сборник задач по высшей математике. 1 курс. – М.: Айрис-пресс, 2004.
Преподаватель Колесова Т.И. Заведующий кафедрой Швецова И.И.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 558. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 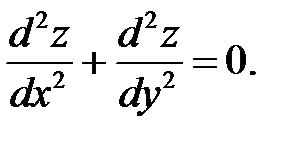
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 Показать, что
Показать, что 
 и две точки
и две точки  и
и  Требуется: 1) вычислить значение
Требуется: 1) вычислить значение  функции в точке
функции в точке  .; 2) вычислить приближенное значение
.; 2) вычислить приближенное значение  функции в точке
функции в точке  функции в точке
функции в точке  , заменив приращение функции при переходе от точки
, заменив приращение функции при переходе от точки  в точке
в точке 
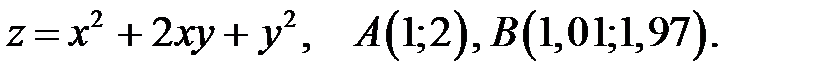

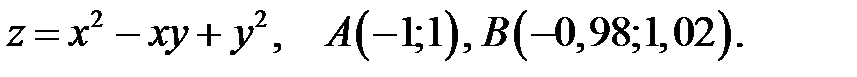





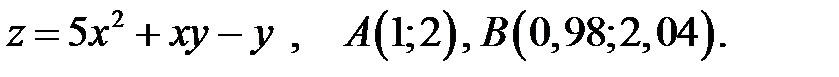


 , заданной системой неравенств.
, заданной системой неравенств.



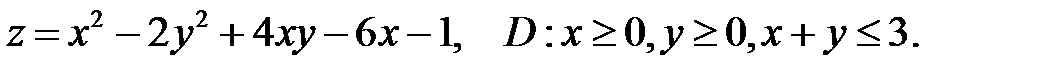





 , точка
, точка  и вектор
и вектор  Найти: 1)
Найти: 1) 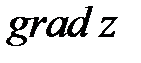 в точке
в точке  .
.





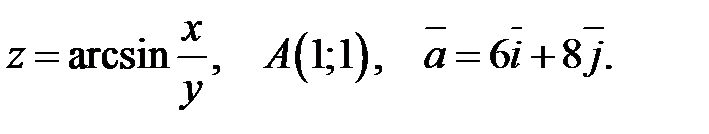

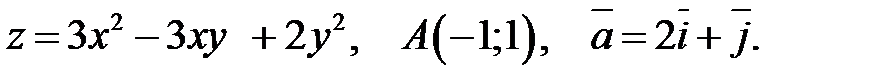



 г)
г) 
 б)
б) 
 г)
г) 
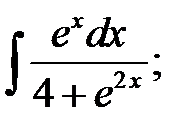 б)
б) 
 г)
г) 
 б)
б) 
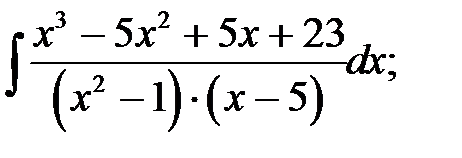 г)
г) 
 б
б 
 г)
г)
 б)
б) 
 г)
г)
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 б)
б) 
 г)
г) 
 и
и 
 и прямой
и прямой 

 и окружностью
и окружностью  .
. фигуры, ограниченной прямой
фигуры, ограниченной прямой  , другой косинусоиды
, другой косинусоиды  и осью
и осью 
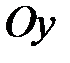 фигуры, ограниченной локоном Аньези
фигуры, ограниченной локоном Аньези  и параболой
и параболой 
 и осью
и осью  от начала координат до точки с абсциссой
от начала координат до точки с абсциссой 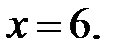

 ,
, 
 .
.