
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Элем-ые ф-ции компл-ой пер-ой:степ-я, пок-я, триг-е, обр-ые триг-е, гипербол-ие
К элем ФКП относ след:  –лин ф-ия –лин ф-ия  -степ-ая -степ-ая  – дробнолин – дробнолин 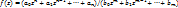 -общ рацион-ая -общ рацион-ая  ф-ия Жуковского а также: 1)показательная ф-ия Жуковского а также: 1)показательная  св-ва: а) св-ва: а)  б) б)  в) в)  явл периодич с периодом явл периодич с периодом 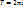 ► ►  ◄ г) ◄ г)  может принимать и отриц знач► может принимать и отриц знач►  ◄2)логарифм ф-ции ◄2)логарифм ф-ции  св-ва аналогичны св-ам lnxза искючением двух: а) lnzмногозначная б) lnzопред для всех zкроме 0 3)тригоном-ие ф-ции св-ва аналогичны св-ам lnxза искючением двух: а) lnzмногозначная б) lnzопред для всех zкроме 0 3)тригоном-ие ф-ции  св-ва аналогичны св-вам действ тригоном функций за исключ след-его: св-ва аналогичны св-вам действ тригоном функций за исключ след-его:  могут быть и больше 1 4)обратн тригонм ф-ции могут быть и больше 1 4)обратн тригонм ф-ции  опр. опр.  комплексного числа zназ комплексное число wsinкоторого равен z { комплексного числа zназ комплексное число wsinкоторого равен z {  }<=> }<=>  , обрат триг ф-ции представл след образом:{ , обрат триг ф-ции представл след образом:{  }-многозначные 5)гиперболические ф-ции }-многозначные 5)гиперболические ф-ции 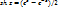 , , 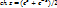 , ,  , ,  , замеч ф-ции shzи chzявл период с наим , замеч ф-ции shzи chzявл период с наим 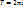 ф-ции thzи cthzпериодич с наим ф-ции thzи cthzпериодич с наим  , ф-лы связи между тригоном и гипербол: , ф-лы связи между тригоном и гипербол:  . .
2.3Производная фкп.Условия Коши-Римана:Будем рассматривать однозначную ФКП. ω =f(z), z=x+iy, ω=u(x,y)+iv(x,y). Пусть ф-ция f(z) определена в окрестности некотор. точки z, придадим ей прирощение  z, z,  ω=f(z+ ω=f(z+  z)-f(z). Опр.:Если сущ. Конечный предел отношения приращения ф-ции к приращению арумента: z)-f(z). Опр.:Если сущ. Конечный предел отношения приращения ф-ции к приращению арумента:  =: =:  , то 1)f(z) назыв. Дефереенцируемой в точке z. 2)предел называется производной ф-ции в точку z. f'(z)= , то 1)f(z) назыв. Дефереенцируемой в точке z. 2)предел называется производной ф-ции в точку z. f'(z)=  (1). Если ф-ция f(z) диференц. в точке z, то она непрерывна в этой точке. Обратное неверно! Ф-цию (1)можно записать и иначе: f'(z)= (1). Если ф-ция f(z) диференц. в точке z, то она непрерывна в этой точке. Обратное неверно! Ф-цию (1)можно записать и иначе: f'(z)=  . Опр.:Ф-ция f(z) наз. Диф. В области D если она диф. В каждой точке этой области. Т(Каши-Римена): Для того чтобы ф-ция ω=f(z) равная u(x,y)+iv(x,y) была диф. в некоторой точке z=x+iy<=> выполнение след. условий: 1)ф-ции u(x,y) и iv(x,y) были деф.в некот. точке (x,y). 2)выплонялись след условия{ . Опр.:Ф-ция f(z) наз. Диф. В области D если она диф. В каждой точке этой области. Т(Каши-Римена): Для того чтобы ф-ция ω=f(z) равная u(x,y)+iv(x,y) была диф. в некоторой точке z=x+iy<=> выполнение след. условий: 1)ф-ции u(x,y) и iv(x,y) были деф.в некот. точке (x,y). 2)выплонялись след условия{  ; ;  }-условие Каши-Римена. При этом производная ф-ции вычисляется по формуле f ‘(z)= }-условие Каши-Римена. При этом производная ф-ции вычисляется по формуле f ‘(z)=  = =  ►Пусть ф-ция f(z) дифер. В точке z. Это озночает что сущ. конечный придел ►Пусть ф-ция f(z) дифер. В точке z. Это озночает что сущ. конечный придел  = =  f ‘(z), т.к. f ‘(z), т.к.  любыми способами, то рассмотрим 2 случая: А) любыми способами, то рассмотрим 2 случая: А)  +i +i  = =  , ,  =0 ; f ‘(z)= =0 ; f ‘(z)=  = =  +i +i  = =  . Б) . Б)  =0, =0,  =i =i  ;f ‘(z)= ;f ‘(z)= 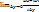
=  + +  = -i = -i 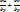 , т.к. придел должен быть 1 и тот же , т.к. придел должен быть 1 и тот же  -i -i 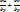 . .  ; ;  ◄ Все основные правила диф. для ф-ции действ. Переменной справедливы и для ФКП. А именно свойства производной:1)(f(z)±g(z)) ' = f ‘(z)±g ‘(z). 2) (f(z)*g(z)) ' = f ‘(z)*g(z)+f (z)*g ‘(z).3)(f(z)/g(z)) '= ◄ Все основные правила диф. для ф-ции действ. Переменной справедливы и для ФКП. А именно свойства производной:1)(f(z)±g(z)) ' = f ‘(z)±g ‘(z). 2) (f(z)*g(z)) ' = f ‘(z)*g(z)+f (z)*g ‘(z).3)(f(z)/g(z)) '=  .4)F(f(z))=F ‘(f(z))*f ‘(z) .4)F(f(z))=F ‘(f(z))*f ‘(z)
2.4Аналитические ф-ции. Гармонические ф-ции.Опр.Ф-ция ω=f(z) однозначная и диф-ая в некот. области D, наз-ся аналитич. в этой области(регулярной, гармонич.)Опр.Точки комплексной области z в которых ф-ция f(z) явл. аналитич, наз-ся регулярными, а точки в которых ф-ция не явл-ся аналитич. наз-ся ососбыми.Опр.Диф-алом аналитич. ф-ции f(z) наз-ся главная часть приращения ф-ции, линейная относит-ноΔ z  .Опр.Ф-ция u=u(x,y) удовлетв. ур-ию Лапласа наз-ся гармонич-ой. Вывод:Действительн и мнимые части аналитич. ф–ции явл-ся гармоничес-ми фун-ями.Опр. Гармонич. ф-ции удовлетвор. условиям Коши-Римона, наз взаимно сопряж-ми. .Опр.Ф-ция u=u(x,y) удовлетв. ур-ию Лапласа наз-ся гармонич-ой. Вывод:Действительн и мнимые части аналитич. ф–ции явл-ся гармоничес-ми фун-ями.Опр. Гармонич. ф-ции удовлетвор. условиям Коши-Римона, наз взаимно сопряж-ми.
2.5Геометрический смысл модуля и аргумента производной.Пусть задана ф-ция  , которая явл аналитической в обл. D, содерж-ая точку , которая явл аналитической в обл. D, содерж-ая точку  причем причем 
 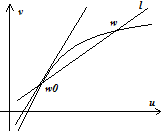

Если  , то секущая занимает полож-е касательной и угол между кас-ой и осью Ox, тогда , то секущая занимает полож-е касательной и угол между кас-ой и осью Ox, тогда  . По опред произв ф-ции в т есть предел отнош-я приращ ф-ции к приращ аргумента: . По опред произв ф-ции в т есть предел отнош-я приращ ф-ции к приращ аргумента:  , ,  - коэф растяжения. Если k>1-растяжение области Dпри отображении. Если k<1- сжатие обл Dпри отображ. - коэф растяжения. Если k>1-растяжение области Dпри отображении. Если k<1- сжатие обл Dпри отображ.
Вывод: геом смысл модуля производной это коэф растяжения  (разность между касат углами при отображ) Вывод: геом смысл аргумента произв в точке состоит в том, что это есть угол на который нужно повернуть касательную к кривой (разность между касат углами при отображ) Вывод: геом смысл аргумента произв в точке состоит в том, что это есть угол на который нужно повернуть касательную к кривой  , для того, чтобы получить направ касательной кривой Lв точке , для того, чтобы получить направ касательной кривой Lв точке  . Таким образом отображ с помощьюааналит-ой ф-ции обладает св-ом консерватизма углов и постоянства растяжения. Такое отображ наз конформным . Таким образом отображ с помощьюааналит-ой ф-ции обладает св-ом консерватизма углов и постоянства растяжения. Такое отображ наз конформным
2.6Интегрирование ф-ций комплексной переменной:Рассмотрим  , для того чтобы интегрирование вдоль любого контура было возможно, необходимо: 1)f(z)-непрерывная ф-ция. 2)контур L- гладкий. , для того чтобы интегрирование вдоль любого контура было возможно, необходимо: 1)f(z)-непрерывная ф-ция. 2)контур L- гладкий.  = =  = =
 +i +i  = = 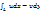 +i +i  =>т.е интеграл от ФКП равен сумме 2-ух криволинейных интегралов 2-го рода: =>т.е интеграл от ФКП равен сумме 2-ух криволинейных интегралов 2-го рода:  = = 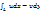 +i +i  . Свойства анологичны св-вам КРИ 2рода: 1) . Свойства анологичны св-вам КРИ 2рода: 1)  = =  . 2) . 2)  =a =a  . 3) . 3)  = =  . 4) . 4)  = =  + +  . Замечание:Если контур Lзадан параметрическими ур. : {x=x(t);y=y(t)},α≤t≤β , то интеграл выглядит так: . Замечание:Если контур Lзадан параметрическими ур. : {x=x(t);y=y(t)},α≤t≤β , то интеграл выглядит так:  = = 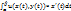 - -  +i +i  + +
 . .
2.7Теоремы КошиТ1(для односвязной области).Если ф-ция f(z) аналитична замкнутой односвязн. области ограниченной контуром L(гладким, замкнутым) прроходимым против часовой стрелки, то интеграл вычислять не надо, он=0.  ►Воспользуемся ф-лой ►Воспользуемся ф-лой  = =  -vdy+i* -vdy+i*  +udyв которой инт-л +udyв которой инт-л  , в силу того, что ф-ции uи vявл. взаимно сопряж. и удовлетв. условиям Коши-Римона , в силу того, что ф-ции uи vявл. взаимно сопряж. и удовлетв. условиям Коши-Римона  = =  ; ;  =- =-  }условия незав-ти каждого из криволин. инт.от пути интегрир-ия◄Т1 (для многосвязн. области). Если ф-ция f(z) аналитична в некоторой многосвязной обл. D, огранич. гладким контуром L, то итеграл по внешнему контуру равен сумме инт-ов по внутренним контурам. Все контуры обходят против часовой стрелки. СледствиеЕсли f(z) аналитичн. в некот. односвязн. области D, то интеграл по любому контуру, лежащему внутри этого контура, не зависит от формы контура, а зависит от нач. и конечн. точки. Это означает, что инт-л от аналитич. ф-ции по разомкнутому контуру може вычисляться по формуле }условия незав-ти каждого из криволин. инт.от пути интегрир-ия◄Т1 (для многосвязн. области). Если ф-ция f(z) аналитична в некоторой многосвязной обл. D, огранич. гладким контуром L, то итеграл по внешнему контуру равен сумме инт-ов по внутренним контурам. Все контуры обходят против часовой стрелки. СледствиеЕсли f(z) аналитичн. в некот. односвязн. области D, то интеграл по любому контуру, лежащему внутри этого контура, не зависит от формы контура, а зависит от нач. и конечн. точки. Это означает, что инт-л от аналитич. ф-ции по разомкнутому контуру може вычисляться по формуле  =F(B)-F(A)=F(z)| =F(B)-F(A)=F(z)|  F(z)-первообразная от f(z), т.е. в этом случае работают все известные методы интегр-ия и табличн. инт-лы. F(z)-первообразная от f(z), т.е. в этом случае работают все известные методы интегр-ия и табличн. инт-лы.
2.8Интегральная ф-ла КошиПусть дана ф-ия  – аналитическая замкнутой обл D(огранич контур L) требуется по знач-ию ф-ции на границ обл по контуру Lнайти знач ф-ции в любой точке внутри обл – аналитическая замкнутой обл D(огранич контур L) требуется по знач-ию ф-ции на границ обл по контуру Lнайти знач ф-ции в любой точке внутри обл 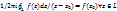 – инт-ая ф-ла Коши, – инт-ая ф-ла Коши,  -инт-л Коши, -инт-л Коши,  –ядро Коши Замеч: Если –ядро Коши Замеч: Если  не принадл D, то ин-л Коши равен 0теорема Обобщенная инт-ая ф-ла Коши: Если не принадл D, то ин-л Коши равен 0теорема Обобщенная инт-ая ф-ла Коши: Если  аналитична замкнутой односвязн обл D, то в каждой точке это й области она диф-ема сколько угодно раз и её производная n-ого порядка опред след ф-лой аналитична замкнутой односвязн обл D, то в каждой точке это й области она диф-ема сколько угодно раз и её производная n-ого порядка опред след ф-лой 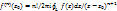 -обобщенна ф-ла Коши. При n=0 получ интегр. ф-лу Коши -обобщенна ф-ла Коши. При n=0 получ интегр. ф-лу Коши
2.9Комплексные числовые и функциональные ряды.Основные понятия:Опр. Числловым рядом будем наз. бесконечную сумму элементов числовой последовательности.  =z1+z2+..+zn+zn+1(1) Опр. Частичной суммой ряда называется сумма n первых его элем. Sn= z1+z2+..+zn , сумму оставшихся элементов принято называть остатком ряда: Rn= zn+1+ zn+2+.. .Опр. ряд (1) назв. Сход. Если сущ. Конечный придел последовательности n-ых частичных сумм ряда =z1+z2+..+zn+zn+1(1) Опр. Частичной суммой ряда называется сумма n первых его элем. Sn= z1+z2+..+zn , сумму оставшихся элементов принято называть остатком ряда: Rn= zn+1+ zn+2+.. .Опр. ряд (1) назв. Сход. Если сущ. Конечный придел последовательности n-ых частичных сумм ряда  =S<∞ и сумма ряда равна S. Справедливы утверждения: 1)для схождения ряда (1) <=> чтобы =S<∞ и сумма ряда равна S. Справедливы утверждения: 1)для схождения ряда (1) <=> чтобы  =0. 2) =0. 2)  = =  +i +i  , т.к. zn=xn+iyn сосотоит из 2-ух рядов то для того чтобы ряд (1) сход. Нужно чтоб сход 2 ряда. 3)Если ряд , т.к. zn=xn+iyn сосотоит из 2-ух рядов то для того чтобы ряд (1) сход. Нужно чтоб сход 2 ряда. 3)Если ряд  сходится, то сходится, то  тоже сходится и наз. абсолютно сход. Все признаки сходимости (необходимый признак, Доломбера , Каши) справедливы и для ряда (1). Опр.Функциональным рядом наз. ряд тоже сходится и наз. абсолютно сход. Все признаки сходимости (необходимый признак, Доломбера , Каши) справедливы и для ряда (1). Опр.Функциональным рядом наз. ряд  (2) элементами которого явл. ФКП. (2) элементами которого явл. ФКП.  =f1(z)+ f2(z)+..+ fn(z)+ fn+1(z)+… =f1(z)+ f2(z)+..+ fn(z)+ fn+1(z)+…
Опр.точка z0 которой соответствует числ. Ряд  и он сходится, назв. Точкой сходимости. Множество всех точек сходимости назв. Облостью сходимости. Опр.Сходящийся в некоторой обл. Dф-ный ряд и он сходится, назв. Точкой сходимости. Множество всех точек сходимости назв. Облостью сходимости. Опр.Сходящийся в некоторой обл. Dф-ный ряд  назв. равномерно сход. в этой области, если ∀ сколь угодно малого ε сущ. такой N=N(ε), что для всех n>N => |Rn(z)|< ε , назв. равномерно сход. в этой области, если ∀ сколь угодно малого ε сущ. такой N=N(ε), что для всех n>N => |Rn(z)|< ε ,  =0. Опр.Степенным рядом назв. ф-ный ряд вида =0. Опр.Степенным рядом назв. ф-ный ряд вида  = =
c0+c1z+c2z2+..+cnzn…(3). Ряд по степеням zв окрестности точки 0:  = =
c0+c1(z-a)+c2(z-a)2+..+cn(z-a)n…Теорема(Абеля):Если степенной ряд сход. в некоторой точку z0≠0, то он обсалютно сходится в круге |z|<|z0|. Причём во всяком круге лежащем внутри круга сходимости |z|<r<|z0|, ряд (3) сходится равномерно.
2.10Ряд Лорана ФКП.Рядом Лорана наз двустор степ ряд  , коэф которого опред ф-лой: , коэф которого опред ф-лой:  Ряд Тейлора явл частным случаем ряда Лорана.Всякую ф-цию f(z) аналитическая в круговом кольце Ряд Тейлора явл частным случаем ряда Лорана.Всякую ф-цию f(z) аналитическая в круговом кольце  м.б. единственным отрезком разложения в нём в ряд Лорана Опр:Точки области Dв которых ф-ция f(z)-аналитична наз правильными. Точки в которых ф-ция не явл аналитичн наз особыми м.б. единственным отрезком разложения в нём в ряд Лорана Опр:Точки области Dв которых ф-ция f(z)-аналитична наз правильными. Точки в которых ф-ция не явл аналитичн наз особыми
2.11Особые точки ф-ции компл. переменного и их классификация Опр.Точки комплексн. пл-ти z наз. правильными для ф-ции f(z), если в них f(z) – аналитич-ая.Опр.Точки в которых f(z) не явл. аналитич-ой наз-ся особой.Опр.Особая точка наз-ся изолированной особой точкой если сущ. окрестность этой точки (круг дост. малого радиуса с ценром в этой точке) в которой данная точка явл. единственной особой точкой. Если (.)z =aявл. изол. особой (.) для f(z), то найдётся достаточно малое кольцо, лежащее в окрестности этой точки, в котором ф-ция f(z) явл. аналитической. Т.к. всякую аналит. в кольце ф-цию можно представить рядом Лорана причём единств. образом, то справедлива ф-ла:f(z)=  + +  -(1) При разложении ф-ции в ряд Лорана могут быть след. случаи: 1) в разложение (1) отсутствует главная частьf(z)= -(1) При разложении ф-ции в ряд Лорана могут быть след. случаи: 1) в разложение (1) отсутствует главная частьf(z)=  = =  )/2 +.. )/2 +..  )/n!. В этом случае (.)z=aназ-ся устранимой особой точкой, доопределив f(z)*b(.)a=>f(a)= )/n!. В этом случае (.)z=aназ-ся устранимой особой точкой, доопределив f(z)*b(.)a=>f(a)=  мы получим аналит-ую ф-цию в (.)a. Определить характер изолир. особой точки можно дргим способом. Если сущ. конечный мы получим аналит-ую ф-цию в (.)a. Определить характер изолир. особой точки можно дргим способом. Если сущ. конечный  f(z)=A!= f(z)=A!=  , то (.)z=a, есть устранимая особая точка.2)Разложение f(z) в ряд Лорана содерж. правая часть и конечное число слогаемых в главной части. f(z)= , то (.)z=a, есть устранимая особая точка.2)Разложение f(z) в ряд Лорана содерж. правая часть и конечное число слогаемых в главной части. f(z)=  + +  , c*m!=0;(.)z=aназ. полюсом порядка m. Если ∃ , c*m!=0;(.)z=aназ. полюсом порядка m. Если ∃  f(z)= f(z)=  то (.)z=aназ-ся полюсом.3)Главная часть (1) содержит бесконечное число слогаемых, в этом случае (.)z=aназ-ся сущ-но особой точкой Замечание: Все типы рассмотренных особых точек явл-ся конечными особыми (.)z=∞ всегдаявл. особой точкой. Характер особой точки в этом случае можно определить для точки обратной (1/z). то (.)z=aназ-ся полюсом.3)Главная часть (1) содержит бесконечное число слогаемых, в этом случае (.)z=aназ-ся сущ-но особой точкой Замечание: Все типы рассмотренных особых точек явл-ся конечными особыми (.)z=∞ всегдаявл. особой точкой. Характер особой точки в этом случае можно определить для точки обратной (1/z).
2.12)Нули аналитических функций, связь между нулями и полюсами: Опр. Точка z=aназ. нулём f(z) если f(a)=0. Точка z=aназ. нулём порядка mесли разложение f(z) в ряд Тейлора в окрестности этой точки имеет вид: f(z)=cm(z-a)m+cm+1(z-a)m+1+…; cm≠0; При m=1 ноль наз. простым. Способ определения порядка 0: Если {f(a)=f ’(a)=f ”(a)=..=
f(m-1)(a)=0; f(m-1)(a)≠0=>точка z=aявл. нулём порядка m}Порядком нуля определяется порядком старшей производной отличной от 0. Теорема 1:Для того чтобы точка z=aявл. нулём порядка mдля f(z) <=> чтобы f(z) имела вид: f(z)=(z-a)m*φ(z) ►=>н)пусть точка z=aноль порядка m тогда справедливо представление : f(z)=cm(z-a)m+cm+1(z-a)m+1+…=
(z-a)m(cm+ cm+1(z-a)+cm+2(z-a)m+..)=(z-a)m* φ(z).<=д) f(z)=(z-a)m*φ(z)=|φ(z)-семетричная ф-ция, то её можно разлож. в ряд Тейлора|=(z-a)m(c0+ c1(z-a)+c2(z-a)2+..)=
c0(z-a)m+c1(z-a)m+1+ c2(z-a)m+2+…;c0≠0. Точка z=aесть нуль порядка m. ◄ Теорема 2: Для того чтобы точка z=a явл. нулём порядка mдля f(z) <=> чтобы она была полюсом порядка m для ф-ции F(z)=  . .
2.13Вычеты: опред, вычисл. Основная теорема о вычетах.Вычетом в конечной изолиров. особой точки наз-ся число равное коэф  (коэф. при первой отрицат. степени при разложение ф-ции в ряд Лоранса) (коэф. при первой отрицат. степени при разложение ф-ции в ряд Лоранса)  = =  = =  ;Resf(a)= ;Resf(a)=  Способы вычисления 1)(.) z=aустранимая особая точка. Resf(a)=0. т.к. разложение f(z) в ряд Лорана и содержит главной части 2)(.)z=a Способы вычисления 1)(.) z=aустранимая особая точка. Resf(a)=0. т.к. разложение f(z) в ряд Лорана и содержит главной части 2)(.)z=a  существенно особая точка Resf(a)= существенно особая точка Resf(a)=  где коэф-нт. где коэф-нт.  определяется из разложения ф-ции в ряд Лорана.3)(.)z=a определяется из разложения ф-ции в ряд Лорана.3)(.)z=a  полюс порядка mResf(a)= полюс порядка mResf(a)=  (f(z-a)^m*f(z)) В частном случае для простого полюса мы получаем:(m=1)Resf(a)= (f(z-a)^m*f(z)) В частном случае для простого полюса мы получаем:(m=1)Resf(a)=  (z-a)f(z).4)Если ф-ция f(z) явл. частным 2-ух ф-ций (z-a)f(z).4)Если ф-ция f(z) явл. частным 2-ух ф-ций  , где , где  !=0, !=0,  =0, =0,  !=0, Resf(z)= !=0, Resf(z)=  в этом случае (.) z=a явл-ся полюсом для ф-ции f(z)Основная теорема о вычетах:Если ф-ция f(z) аналитична в некоторой области D огранич. гладким замкн. контуром L, ориентированным положительно в обл. D, а так же и на самом контуре Lза исключ. конечного числа точек a1, a2,…,ak , лежащих в обл. D, то интеграл в этом случае (.) z=a явл-ся полюсом для ф-ции f(z)Основная теорема о вычетах:Если ф-ция f(z) аналитична в некоторой области D огранич. гладким замкн. контуром L, ориентированным положительно в обл. D, а так же и на самом контуре Lза исключ. конечного числа точек a1, a2,…,ak , лежащих в обл. D, то интеграл  будет равен сумме вычетов относительно всех особых точек, умноженой на 2πi: будет равен сумме вычетов относительно всех особых точек, умноженой на 2πi:  =2πi* =2πi*  ►Для док-ва восп. след. формулой: (1) ►Для док-ва восп. след. формулой: (1)  ={0, m≠-1; 2πi ,m≠-1}. Если точка z=aявл. изолир. особой точкой для ф-ции f(z) аналитичной в некот. Обл., то в окрестности этой точки f(z) можно разложить в ряд Лорана: f(z)= ={0, m≠-1; 2πi ,m≠-1}. Если точка z=aявл. изолир. особой точкой для ф-ции f(z) аналитичной в некот. Обл., то в окрестности этой точки f(z) можно разложить в ряд Лорана: f(z)=  + +  . Проинтегрируем этот ряд по малому замкнутому контуру внутри кольца: . Проинтегрируем этот ряд по малому замкнутому контуру внутри кольца:  =|(1)|= 2πi* =|(1)|= 2πi*  =>В правой части на основании (1) все интегралы будут равны 0 кроме одного=> =>В правой части на основании (1) все интегралы будут равны 0 кроме одного=>  =Resf(a)= =Resf(a)=  . Воспользуемся теоремой Каши для многосвязной области в силу которой справедливо след. Равенство: . Воспользуемся теоремой Каши для многосвязной области в силу которой справедливо след. Равенство:  = =  =2πi =2πi  =2πi =2πi  ◄ ◄
|


 –лин ф-ия
–лин ф-ия  -степ-ая
-степ-ая  – дробнолин
– дробнолин 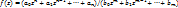 -общ рацион-ая
-общ рацион-ая  ф-ия Жуковского а также: 1)показательная
ф-ия Жуковского а также: 1)показательная  св-ва: а)
св-ва: а)  б)
б)  в)
в)  явл периодич с периодом
явл периодич с периодом 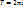 ►
►  ◄ г)
◄ г)  ◄2)логарифм ф-ции
◄2)логарифм ф-ции  св-ва аналогичны св-ам lnxза искючением двух: а) lnzмногозначная б) lnzопред для всех zкроме 0 3)тригоном-ие ф-ции
св-ва аналогичны св-ам lnxза искючением двух: а) lnzмногозначная б) lnzопред для всех zкроме 0 3)тригоном-ие ф-ции  св-ва аналогичны св-вам действ тригоном функций за исключ след-его:
св-ва аналогичны св-вам действ тригоном функций за исключ след-его:  могут быть и больше 1 4)обратн тригонм ф-ции
могут быть и больше 1 4)обратн тригонм ф-ции  опр.
опр.  комплексного числа zназ комплексное число wsinкоторого равен z {
комплексного числа zназ комплексное число wsinкоторого равен z {  }<=>
}<=>  , обрат триг ф-ции представл след образом:{
, обрат триг ф-ции представл след образом:{  }-многозначные 5)гиперболические ф-ции
}-многозначные 5)гиперболические ф-ции 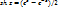 ,
, 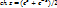 ,
,  ,
,  , замеч ф-ции shzи chzявл период с наим
, замеч ф-ции shzи chzявл период с наим  , ф-лы связи между тригоном и гипербол:
, ф-лы связи между тригоном и гипербол:  .
. z,
z,  =:
=:  , то 1)f(z) назыв. Дефереенцируемой в точке z. 2)предел называется производной ф-ции в точку z. f'(z)=
, то 1)f(z) назыв. Дефереенцируемой в точке z. 2)предел называется производной ф-ции в точку z. f'(z)=  . Опр.:Ф-ция f(z) наз. Диф. В области D если она диф. В каждой точке этой области. Т(Каши-Римена): Для того чтобы ф-ция ω=f(z) равная u(x,y)+iv(x,y) была диф. в некоторой точке z=x+iy<=> выполнение след. условий: 1)ф-ции u(x,y) и iv(x,y) были деф.в некот. точке (x,y). 2)выплонялись след условия{
. Опр.:Ф-ция f(z) наз. Диф. В области D если она диф. В каждой точке этой области. Т(Каши-Римена): Для того чтобы ф-ция ω=f(z) равная u(x,y)+iv(x,y) была диф. в некоторой точке z=x+iy<=> выполнение след. условий: 1)ф-ции u(x,y) и iv(x,y) были деф.в некот. точке (x,y). 2)выплонялись след условия{  ;
;  }-условие Каши-Римена. При этом производная ф-ции вычисляется по формуле f ‘(z)=
}-условие Каши-Римена. При этом производная ф-ции вычисляется по формуле f ‘(z)=  =
=  ►Пусть ф-ция f(z) дифер. В точке z. Это озночает что сущ. конечный придел
►Пусть ф-ция f(z) дифер. В точке z. Это озночает что сущ. конечный придел  f ‘(z), т.к.
f ‘(z), т.к.  любыми способами, то рассмотрим 2 случая: А)
любыми способами, то рассмотрим 2 случая: А)  +i
+i  =
=  ,
,  =
=  +i
+i  =
=  =0,
=0,  =i
=i  ;f ‘(z)=
;f ‘(z)= 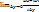
 +
+  = -i
= -i 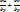 , т.к. придел должен быть 1 и тот же
, т.к. придел должен быть 1 и тот же  -i
-i  .4)F(f(z))=F ‘(f(z))*f ‘(z)
.4)F(f(z))=F ‘(f(z))*f ‘(z) .Опр.Ф-ция u=u(x,y) удовлетв. ур-ию Лапласа наз-ся гармонич-ой. Вывод:Действительн и мнимые части аналитич. ф–ции явл-ся гармоничес-ми фун-ями.Опр. Гармонич. ф-ции удовлетвор. условиям Коши-Римона, наз взаимно сопряж-ми.
.Опр.Ф-ция u=u(x,y) удовлетв. ур-ию Лапласа наз-ся гармонич-ой. Вывод:Действительн и мнимые части аналитич. ф–ции явл-ся гармоничес-ми фун-ями.Опр. Гармонич. ф-ции удовлетвор. условиям Коши-Римона, наз взаимно сопряж-ми. , которая явл аналитической в обл. D, содерж-ая точку
, которая явл аналитической в обл. D, содерж-ая точку  причем
причем 



 , то секущая занимает полож-е касательной и угол между кас-ой и осью Ox, тогда
, то секущая занимает полож-е касательной и угол между кас-ой и осью Ox, тогда  . По опред произв ф-ции в т есть предел отнош-я приращ ф-ции к приращ аргумента:
. По опред произв ф-ции в т есть предел отнош-я приращ ф-ции к приращ аргумента:  ,
,  - коэф растяжения. Если k>1-растяжение области Dпри отображении. Если k<1- сжатие обл Dпри отображ.
- коэф растяжения. Если k>1-растяжение области Dпри отображении. Если k<1- сжатие обл Dпри отображ. (разность между касат углами при отображ) Вывод: геом смысл аргумента произв в точке состоит в том, что это есть угол на который нужно повернуть касательную к кривой
(разность между касат углами при отображ) Вывод: геом смысл аргумента произв в точке состоит в том, что это есть угол на который нужно повернуть касательную к кривой  , для того, чтобы получить направ касательной кривой Lв точке
, для того, чтобы получить направ касательной кривой Lв точке  . Таким образом отображ с помощьюааналит-ой ф-ции обладает св-ом консерватизма углов и постоянства растяжения. Такое отображ наз конформным
. Таким образом отображ с помощьюааналит-ой ф-ции обладает св-ом консерватизма углов и постоянства растяжения. Такое отображ наз конформным , для того чтобы интегрирование вдоль любого контура было возможно, необходимо: 1)f(z)-непрерывная ф-ция. 2)контур L- гладкий.
, для того чтобы интегрирование вдоль любого контура было возможно, необходимо: 1)f(z)-непрерывная ф-ция. 2)контур L- гладкий.  =
= +i
+i  =
= 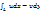 +i
+i  =>т.е интеграл от ФКП равен сумме 2-ух криволинейных интегралов 2-го рода:
=>т.е интеграл от ФКП равен сумме 2-ух криволинейных интегралов 2-го рода:  =
=  . 2)
. 2)  =a
=a  . 4)
. 4)  =
=  +
+  . Замечание:Если контур Lзадан параметрическими ур. : {x=x(t);y=y(t)},α≤t≤β , то интеграл выглядит так:
. Замечание:Если контур Lзадан параметрическими ур. : {x=x(t);y=y(t)},α≤t≤β , то интеграл выглядит так: 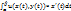 -
-  +i
+i  +
+ .
. ►Воспользуемся ф-лой
►Воспользуемся ф-лой  =
=  -vdy+i*
-vdy+i*  , в силу того, что ф-ции uи vявл. взаимно сопряж. и удовлетв. условиям Коши-Римона
, в силу того, что ф-ции uи vявл. взаимно сопряж. и удовлетв. условиям Коши-Римона  =
=  ;
;  =-
=-  }условия незав-ти каждого из криволин. инт.от пути интегрир-ия◄Т1 (для многосвязн. области). Если ф-ция f(z) аналитична в некоторой многосвязной обл. D, огранич. гладким контуром L, то итеграл по внешнему контуру равен сумме инт-ов по внутренним контурам. Все контуры обходят против часовой стрелки. СледствиеЕсли f(z) аналитичн. в некот. односвязн. области D, то интеграл по любому контуру, лежащему внутри этого контура, не зависит от формы контура, а зависит от нач. и конечн. точки. Это означает, что инт-л от аналитич. ф-ции по разомкнутому контуру може вычисляться по формуле
}условия незав-ти каждого из криволин. инт.от пути интегрир-ия◄Т1 (для многосвязн. области). Если ф-ция f(z) аналитична в некоторой многосвязной обл. D, огранич. гладким контуром L, то итеграл по внешнему контуру равен сумме инт-ов по внутренним контурам. Все контуры обходят против часовой стрелки. СледствиеЕсли f(z) аналитичн. в некот. односвязн. области D, то интеграл по любому контуру, лежащему внутри этого контура, не зависит от формы контура, а зависит от нач. и конечн. точки. Это означает, что инт-л от аналитич. ф-ции по разомкнутому контуру може вычисляться по формуле  =F(B)-F(A)=F(z)|
=F(B)-F(A)=F(z)|  F(z)-первообразная от f(z), т.е. в этом случае работают все известные методы интегр-ия и табличн. инт-лы.
F(z)-первообразная от f(z), т.е. в этом случае работают все известные методы интегр-ия и табличн. инт-лы. – аналитическая замкнутой обл D(огранич контур L) требуется по знач-ию ф-ции на границ обл по контуру Lнайти знач ф-ции в любой точке внутри обл
– аналитическая замкнутой обл D(огранич контур L) требуется по знач-ию ф-ции на границ обл по контуру Lнайти знач ф-ции в любой точке внутри обл 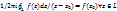 – инт-ая ф-ла Коши,
– инт-ая ф-ла Коши,  -инт-л Коши,
-инт-л Коши,  –ядро Коши Замеч: Если
–ядро Коши Замеч: Если 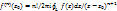 -обобщенна ф-ла Коши. При n=0 получ интегр. ф-лу Коши
-обобщенна ф-ла Коши. При n=0 получ интегр. ф-лу Коши =z1+z2+..+zn+zn+1(1) Опр. Частичной суммой ряда называется сумма n первых его элем. Sn= z1+z2+..+zn , сумму оставшихся элементов принято называть остатком ряда: Rn= zn+1+ zn+2+.. .Опр. ряд (1) назв. Сход. Если сущ. Конечный придел последовательности n-ых частичных сумм ряда
=z1+z2+..+zn+zn+1(1) Опр. Частичной суммой ряда называется сумма n первых его элем. Sn= z1+z2+..+zn , сумму оставшихся элементов принято называть остатком ряда: Rn= zn+1+ zn+2+.. .Опр. ряд (1) назв. Сход. Если сущ. Конечный придел последовательности n-ых частичных сумм ряда  =S<∞ и сумма ряда равна S. Справедливы утверждения: 1)для схождения ряда (1) <=> чтобы
=S<∞ и сумма ряда равна S. Справедливы утверждения: 1)для схождения ряда (1) <=> чтобы  =0. 2)
=0. 2)  +i
+i  , т.к. zn=xn+iyn сосотоит из 2-ух рядов то для того чтобы ряд (1) сход. Нужно чтоб сход 2 ряда. 3)Если ряд
, т.к. zn=xn+iyn сосотоит из 2-ух рядов то для того чтобы ряд (1) сход. Нужно чтоб сход 2 ряда. 3)Если ряд  сходится, то
сходится, то  (2) элементами которого явл. ФКП.
(2) элементами которого явл. ФКП.  и он сходится, назв. Точкой сходимости. Множество всех точек сходимости назв. Облостью сходимости. Опр.Сходящийся в некоторой обл. Dф-ный ряд
и он сходится, назв. Точкой сходимости. Множество всех точек сходимости назв. Облостью сходимости. Опр.Сходящийся в некоторой обл. Dф-ный ряд  =0. Опр.Степенным рядом назв. ф-ный ряд вида
=0. Опр.Степенным рядом назв. ф-ный ряд вида  =
= =
= , коэф которого опред ф-лой:
, коэф которого опред ф-лой:  Ряд Тейлора явл частным случаем ряда Лорана.Всякую ф-цию f(z) аналитическая в круговом кольце
Ряд Тейлора явл частным случаем ряда Лорана.Всякую ф-цию f(z) аналитическая в круговом кольце  м.б. единственным отрезком разложения в нём в ряд Лорана Опр:Точки области Dв которых ф-ция f(z)-аналитична наз правильными. Точки в которых ф-ция не явл аналитичн наз особыми
м.б. единственным отрезком разложения в нём в ряд Лорана Опр:Точки области Dв которых ф-ция f(z)-аналитична наз правильными. Точки в которых ф-ция не явл аналитичн наз особыми +
+  -(1) При разложении ф-ции в ряд Лорана могут быть след. случаи: 1) в разложение (1) отсутствует главная частьf(z)=
-(1) При разложении ф-ции в ряд Лорана могут быть след. случаи: 1) в разложение (1) отсутствует главная частьf(z)=  )/2 +..
)/2 +..  )/n!. В этом случае (.)z=aназ-ся устранимой особой точкой, доопределив f(z)*b(.)a=>f(a)=
)/n!. В этом случае (.)z=aназ-ся устранимой особой точкой, доопределив f(z)*b(.)a=>f(a)=  мы получим аналит-ую ф-цию в (.)a. Определить характер изолир. особой точки можно дргим способом. Если сущ. конечный
мы получим аналит-ую ф-цию в (.)a. Определить характер изолир. особой точки можно дргим способом. Если сущ. конечный  f(z)=A!=
f(z)=A!=  , то (.)z=a, есть устранимая особая точка.2)Разложение f(z) в ряд Лорана содерж. правая часть и конечное число слогаемых в главной части. f(z)=
, то (.)z=a, есть устранимая особая точка.2)Разложение f(z) в ряд Лорана содерж. правая часть и конечное число слогаемых в главной части. f(z)=  , c*m!=0;(.)z=aназ. полюсом порядка m. Если ∃
, c*m!=0;(.)z=aназ. полюсом порядка m. Если ∃  то (.)z=aназ-ся полюсом.3)Главная часть (1) содержит бесконечное число слогаемых, в этом случае (.)z=aназ-ся сущ-но особой точкой Замечание: Все типы рассмотренных особых точек явл-ся конечными особыми (.)z=∞ всегдаявл. особой точкой. Характер особой точки в этом случае можно определить для точки обратной (1/z).
то (.)z=aназ-ся полюсом.3)Главная часть (1) содержит бесконечное число слогаемых, в этом случае (.)z=aназ-ся сущ-но особой точкой Замечание: Все типы рассмотренных особых точек явл-ся конечными особыми (.)z=∞ всегдаявл. особой точкой. Характер особой точки в этом случае можно определить для точки обратной (1/z). .
. (коэф. при первой отрицат. степени при разложение ф-ции в ряд Лоранса)
(коэф. при первой отрицат. степени при разложение ф-ции в ряд Лоранса)  =
=  =
=  существенно особая точка Resf(a)=
существенно особая точка Resf(a)=  (f(z-a)^m*f(z)) В частном случае для простого полюса мы получаем:(m=1)Resf(a)=
(f(z-a)^m*f(z)) В частном случае для простого полюса мы получаем:(m=1)Resf(a)=  (z-a)f(z).4)Если ф-ция f(z) явл. частным 2-ух ф-ций
(z-a)f(z).4)Если ф-ция f(z) явл. частным 2-ух ф-ций  , где
, где  !=0,
!=0,  =0,
=0,  !=0, Resf(z)=
!=0, Resf(z)=  в этом случае (.) z=a явл-ся полюсом для ф-ции f(z)Основная теорема о вычетах:Если ф-ция f(z) аналитична в некоторой области D огранич. гладким замкн. контуром L, ориентированным положительно в обл. D, а так же и на самом контуре Lза исключ. конечного числа точек a1, a2,…,ak , лежащих в обл. D, то интеграл
в этом случае (.) z=a явл-ся полюсом для ф-ции f(z)Основная теорема о вычетах:Если ф-ция f(z) аналитична в некоторой области D огранич. гладким замкн. контуром L, ориентированным положительно в обл. D, а так же и на самом контуре Lза исключ. конечного числа точек a1, a2,…,ak , лежащих в обл. D, то интеграл  будет равен сумме вычетов относительно всех особых точек, умноженой на 2πi:
будет равен сумме вычетов относительно всех особых точек, умноженой на 2πi:  ►Для док-ва восп. след. формулой: (1)
►Для док-ва восп. след. формулой: (1)  ={0, m≠-1; 2πi ,m≠-1}. Если точка z=aявл. изолир. особой точкой для ф-ции f(z) аналитичной в некот. Обл., то в окрестности этой точки f(z) можно разложить в ряд Лорана: f(z)=
={0, m≠-1; 2πi ,m≠-1}. Если точка z=aявл. изолир. особой точкой для ф-ции f(z) аналитичной в некот. Обл., то в окрестности этой точки f(z) можно разложить в ряд Лорана: f(z)=  +
+  . Проинтегрируем этот ряд по малому замкнутому контуру внутри кольца:
. Проинтегрируем этот ряд по малому замкнутому контуру внутри кольца:  =|(1)|= 2πi*
=|(1)|= 2πi*  =>В правой части на основании (1) все интегралы будут равны 0 кроме одного=>
=>В правой части на основании (1) все интегралы будут равны 0 кроме одного=>  . Воспользуемся теоремой Каши для многосвязной области в силу которой справедливо след. Равенство:
. Воспользуемся теоремой Каши для многосвязной области в силу которой справедливо след. Равенство:  =2πi
=2πi  =2πi
=2πi