
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Степенные ряды.Теорема Абеля. Радиус и интерал сход степенного ряда, св-ва.
Знакоперем ряды. Абсолют и условн сходимость. Св-ва абсолютно сход рядов
Опр:Числовой ряд  наз. знакоперем, если среди его элементов имеются как полож так и отрицательные. Опр:Если знакополож ряды могут сход и расход, то знакопеременный ряд наз абсолютносходящимся, если ряд составленный из модулей или абсолютнх величин наз. знакоперем, если среди его элементов имеются как полож так и отрицательные. Опр:Если знакополож ряды могут сход и расход, то знакопеременный ряд наз абсолютносходящимся, если ряд составленный из модулей или абсолютнх величин  сход Опр: Ряд сход Опр: Ряд  наз условносходящимся если ряд из абсолютных величин наз условносходящимся если ряд из абсолютных величин  расход, а расход, а  сход по какому-либо признаку. Для исследования знакоперем рядов на условную сходимость используются признаки Дирихле и Абеля.Св-ва(знакоперем):1)если ряд сход по какому-либо признаку. Для исследования знакоперем рядов на условную сходимость используются признаки Дирихле и Абеля.Св-ва(знакоперем):1)если ряд  сходится абсолютно то он будет абсолютно сходящимся, при любой перестановке его элементов, при этом сумма ряда не изменится 2) Если ряд сходится абсолютно то он будет абсолютно сходящимся, при любой перестановке его элементов, при этом сумма ряда не изменится 2) Если ряд  сход условно то ряд получ из него перестановкой каких-либо элементов может сход (но в другой сумме), а может и расход. Св-ва(абсолютно сход рядов):Если ряд абсолютно сход и имеет сумму S, то ряд, получ из него перестаановкой членов, также сход и имеет ту же сумму S, что и исходный ряд. Абсолютно сход ряды можно почленно складывать и перемножать. сход условно то ряд получ из него перестановкой каких-либо элементов может сход (но в другой сумме), а может и расход. Св-ва(абсолютно сход рядов):Если ряд абсолютно сход и имеет сумму S, то ряд, получ из него перестаановкой членов, также сход и имеет ту же сумму S, что и исходный ряд. Абсолютно сход ряды можно почленно складывать и перемножать.
5.Знакочередующиеся ряды. Признак Лейбница:Знакочеред. рядом назыв. ряд вида:  =a1-a2+a3-a4+… ; an≥0, ∀n. Признак Лейбница: если в знакочеред. Ряде элем. таковы, что выполн.условия: 1) a1>a2>a3>…>an>… 2) =a1-a2+a3-a4+… ; an≥0, ∀n. Признак Лейбница: если в знакочеред. Ряде элем. таковы, что выполн.условия: 1) a1>a2>a3>…>an>… 2)  =0 , то ряд =0 , то ряд  сход. и его сумма положительная и непревосходит первого элем.: 0<S<a1 (S= сход. и его сумма положительная и непревосходит первого элем.: 0<S<a1 (S=  ) ►Докажем, что сущ. ) ►Докажем, что сущ.  =S >0, где Sn= a1-a2+a3…+(-1)n+1an =S >0, где Sn= a1-a2+a3…+(-1)n+1an  , т.к. , т.к.  >0, то Sn>0,∀n. >0, то Sn>0,∀n.
{Sn}(возрастающ. послед.) ,  =a1-(a2-a3)-( a4-a5)…-a2m<a1 , S2m<a1 , послед-ть {Sn}положительна, возрастает и непревосходит a1, тоесть ограничена сверху, а значит имеет предел, т.к. сущ. =a1-(a2-a3)-( a4-a5)…-a2m<a1 , S2m<a1 , послед-ть {Sn}положительна, возрастает и непревосходит a1, тоесть ограничена сверху, а значит имеет предел, т.к. сущ.  =S =>сущ. . =S =>сущ. .  =. =.  S=>сущ. . S=>сущ. .  =S>0, S<a1.◄ =S>0, S<a1.◄
6.Функцион. ряды. Основн. понятия. Признак Вейерштрасса.Опр.Функцион. рядом наз-ся ряд вида  где где  (x)–фун-ции определённые на множ-ве X. Опр.Возьмем (x)–фун-ции определённые на множ-ве X. Опр.Возьмем  ∈X и подставим в ∈X и подставим в  , ,  получим числовой ряд, если он сход-ся, то говорят что получим числовой ряд, если он сход-ся, то говорят что  является точкой сход-ти ф.р является точкой сход-ти ф.р  Опр.Совокупность всех x∈Xпри котором ф.р. сход. наз-ся областью сходимости(D). Суммой ф.р.(1) наз-ся ф-ция S(x) = Опр.Совокупность всех x∈Xпри котором ф.р. сход. наз-ся областью сходимости(D). Суммой ф.р.(1) наз-ся ф-ция S(x) =  (x), эта ф-ция определена для любых x∈D.Признак Вейер-сса.Пусть задан Ф.Р. (x), эта ф-ция определена для любых x∈D.Признак Вейер-сса.Пусть задан Ф.Р.  Если члены ряда удовлетвор. нер-ву Если члены ряда удовлетвор. нер-ву  <= <=  где где  - члены сход., знакополож. числового ряда, то ряд - члены сход., знакополож. числового ряда, то ряд  сход. равномерно и абсолютно, на области D. сход. равномерно и абсолютно, на области D.
Степенные ряды.Теорема Абеля. Радиус и интерал сход степенного ряда, св-ва.
 где где  –числа назыв коэффиц ряда наз степенными рядами. Ряд (1) наз рядом по степеням x, ряд (2)- рядом по степ –числа назыв коэффиц ряда наз степенными рядами. Ряд (1) наз рядом по степеням x, ряд (2)- рядом по степ 
Ряд(1) всегда сход по крайней мере в 1 точке x=0, а ряд 2 – в точке x=  . Ряд (2) с помощью замены . Ряд (2) с помощью замены  сводится к ряду (1), поэтому будем рассматривать ряд (1) сводится к ряду (1), поэтому будем рассматривать ряд (1)
Теорема Абеля: Пусть ряд  сход в некоторой точке сход в некоторой точке  , тогда он сход абсолютно для любого xудовл-его неравенству , тогда он сход абсолютно для любого xудовл-его неравенству  и равномерно для любого xудовл и равномерно для любого xудовл  где gнекоторое число. Если же ряд расход в точке где gнекоторое число. Если же ряд расход в точке  , то он будет расход для всех x удовл нер-во , то он будет расход для всех x удовл нер-во  ►Пусть степ-ой ряд сход в т. ►Пусть степ-ой ряд сход в т.  => =>  =>по необход признаку сравн сход =>по необход признаку сравн сход  . Согласно св-м сходимости послед-ей , после-ть . Согласно св-м сходимости послед-ей , после-ть  будет ограничена, т.е. ∃ M>0, что будет ограничена, т.е. ∃ M>0, что  преобраз исходн ряд след образом преобраз исходн ряд след образом  . С учетом нер-ва . С учетом нер-ва  получ след нер-ва получ след нер-ва  (3)пусть (3)пусть  , тогда , тогда  , ,  будет геом прогрессией со знаменателем будет геом прогрессией со знаменателем  будет сходиться. И из нер-ва (3) и признака сравн следует что ряд будет сходиться. И из нер-ва (3) и признака сравн следует что ряд  сход абсолютно◄Радиус сход для степ ряда (1): 1) применим признак Даламбера сход абсолютно◄Радиус сход для степ ряда (1): 1) применим признак Даламбера  2)прим радикальный призн Коши: 2)прим радикальный призн Коши: 
Правило нах интер-ла сход-ти для степ ряда (1):а)Нах радиус сход б)составим инт-л сход-ти в)Определим сход-ть на концах инт-ла  г) записываем оконч ответ г) записываем оконч ответ
Правило нах интер-ла сход-ти для степ ряда (2): а)Нах радиус сход б)составим инт-л сход-ти  в) исслед сход на концах инт-ла в) исслед сход на концах инт-ла  г) записываем оконч ответ Св-ва:Степенные ряды внутри инт-ла сход можно складывать,перемножать, диф-вать и интегрировать г) записываем оконч ответ Св-ва:Степенные ряды внутри инт-ла сход можно складывать,перемножать, диф-вать и интегрировать
8.Ряды Тейлора и Маклорена. Разложение некот. Элементарных ф-ций:Если f(x) (n+1)раз непрывно диференц. в окрестности некоторой точки x=x0, то ф-цию можно представить рядом Тейлора: f(x)=f(x0)+  (x-x0)+ (x-x0)+  (x-x0)2+…+ (x-x0)2+…+  (x-x0)n+Rn(x); (x-x0)n+Rn(x);
Rn(x)=  f(c); x0<c<x. Если x0=0, то получ. Частный случ. Ф-ции Тейлора, а именно ф-ция Маклорена: f(x)=Pn(x)+Rn(x) , если f(c); x0<c<x. Если x0=0, то получ. Частный случ. Ф-ции Тейлора, а именно ф-ция Маклорена: f(x)=Pn(x)+Rn(x) , если  =0, то =0, то  = =  =f(x), то из ф-ции Тейлора получ. ряд Тейлора, т.к. Pn(x) представляет собой n-ую частичную сумму. Т:Для того чтобы ряд Тейлора сходился и его сумма S(x)=f(x) <=> чтобы =f(x), то из ф-ции Тейлора получ. ряд Тейлора, т.к. Pn(x) представляет собой n-ую частичную сумму. Т:Для того чтобы ряд Тейлора сходился и его сумма S(x)=f(x) <=> чтобы  =0. Замечания: Если =0. Замечания: Если  ≠0, то ряд Тейлора непредставляет ф-цию f(x), хотя может и сходиться(но в другой ф-ции). Опр:Рядом Маклорена называют частный случай ряда Тейлора, или ряд по степеням x, т.е. x0=0. Разложение в ряд Тейлора: 1)sinx= ≠0, то ряд Тейлора непредставляет ф-цию f(x), хотя может и сходиться(но в другой ф-ции). Опр:Рядом Маклорена называют частный случай ряда Тейлора, или ряд по степеням x, т.е. x0=0. Разложение в ряд Тейлора: 1)sinx=  - -  + +  -…= -…=  ;Найти интервал сходимости: ;Найти интервал сходимости:  =x2* =x2*  =0<1 – сход. ∀x ∈ R -> интервал сход. (-∞;∞). 2)sinx=1- =0<1 – сход. ∀x ∈ R -> интервал сход. (-∞;∞). 2)sinx=1-  + +  +…= +…=  ;Интервал сходимости ноход. Так же как и в 1 и он представляет собой всю сисловую ось (-∞;∞). 3) ;Интервал сходимости ноход. Так же как и в 1 и он представляет собой всю сисловую ось (-∞;∞). 3)  = =  ; Интервал сход. (-∞;∞). 4)shx= ; Интервал сход. (-∞;∞). 4)shx=  , chx= , chx=  ; shx= ; shx=  *2( *2(  + +  + +  +…+ +…+  ), (-∞;∞);chx= ), (-∞;∞);chx=  + +  + +  +…+ +…+  , (-∞;∞). 5) , (-∞;∞). 5)  = =  =1+x+x2+..+xn+… ,|x|<1 (-1;1); =1+x+x2+..+xn+… ,|x|<1 (-1;1);  =1-x+x2-x3= =1-x+x2-x3=  , (-1;1). 6) , (-1;1). 6)  =- =-  =- =-  - -  ) )  =- =-  ; |x|<1, [-1;1). ; |x|<1, [-1;1).
9.Применение рядов к приближённым вычислением.С помощью степенных рядов можно решить задачу связанную с прибл. вычисл. с любой наперёд заданной степенью точности. вычисл. ф-ций. Пусть требуется выч-ить знач. ф-ции f(x) с заданной степенью точностиE. Предположим, что ф-цию можно разложить в степ. ряд  Взяв достаточное число первых членов ряда, получим приближ. рав-во Взяв достаточное число первых членов ряда, получим приближ. рав-во  Точность этого рав-ва увелич-ся с возрастанием n. Для того чтобы обеспеч. заданную точность, мы оцениваем по модулю одно из слогаемых ряда, которое меньше Eи берём сумму предыдущих элементов ряда. вычисл. интегр. Точность этого рав-ва увелич-ся с возрастанием n. Для того чтобы обеспеч. заданную точность, мы оцениваем по модулю одно из слогаемых ряда, которое меньше Eи берём сумму предыдущих элементов ряда. вычисл. интегр.  ,E= ,E=  , разложим подынтегральную функциюв степенной ряд , разложим подынтегральную функциюв степенной ряд  =1+t/1! +t^2/2!+…+t^n/n!+.. Вместо заданной подынтегральной функции будем интегрировать в заданных пределах степенной ряд.Отбрасывая все члены ряда, которые больше E, после подстановки пределов интегрирования, получим =1+t/1! +t^2/2!+…+t^n/n!+.. Вместо заданной подынтегральной функции будем интегрировать в заданных пределах степенной ряд.Отбрасывая все члены ряда, которые больше E, после подстановки пределов интегрирования, получим  =(x+ =(x+  )| )|  =(1-1/3+1/10-1/42+(1/216)<E-..) =(1-1/3+1/10-1/42+(1/216)<E-..)  1-1/3+1/10-1/42=0,743.вычисл. диф. урав.y”=F(x,y,y’), {y( 1-1/3+1/10-1/42=0,743.вычисл. диф. урав.y”=F(x,y,y’), {y(  )= )=  ; y’( ; y’(  )= )=  } –нач. усл; } –нач. усл;  - заданные знач. Будем искать решен. д.у. y(x) в виде степенного ряда (*) - y(x)=y( - заданные знач. Будем искать решен. д.у. y(x) в виде степенного ряда (*) - y(x)=y(  )+ )+  *(x- *(x-  )+ )+ 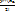 *(x- *(x-  )^2+.. Находим коэф. данного ряда y( )^2+.. Находим коэф. данного ряда y(  )= )=  ; y’( ; y’(  )= )=  ; y’’( ; y’’(  )= )=  ;y’’’( ;y’’’(  )=… Найдя полученн. знач. и подставив их в ряд(*) мы получим решение исходного ду. )=… Найдя полученн. знач. и подставив их в ряд(*) мы получим решение исходного ду.
10.Ряды Фурье периодических ф-ций , вычисл. коэффиц.Теорема ДирихлеОпр. Ф-ция f(x) наз-ся периодич. если сущ. такое полож. число T, что рав-во f(x+T)=f(x), T-период.Опр.Тригонометрич ряд наз-ся ряд вида  + +  (1).Для вычисл-ия коэф. тригон ряда нам нужны некот. ф-лы (1).Для вычисл-ия коэф. тригон ряда нам нужны некот. ф-лы  = =  = =  ; ;  = =  ; ;
 = =  ; ;  = =  все эти ф-лы = (2) все эти ф-лы = (2)
Опр.Рядом Фурье наз-ся тригоном ряд вида (1) коэф. которого опред-ся.форм-ми (2).Теорема ДирихлеЕсли ф-ция f(x) приод-кая с T=2  на интервале [- на интервале [-  ], иудовлетв. условиям:1)кусочно-монотонная, т.е. может иметь конечное число точек разрыва первого рода. 2)кусочно-монотонна, то ряд Фурье сход-ся и его сумма равна самой ф-цииS(x)=f(x) в т. непрерывности, а в т. разрыва, сумма будет равна S(x) = (f( ], иудовлетв. условиям:1)кусочно-монотонная, т.е. может иметь конечное число точек разрыва первого рода. 2)кусочно-монотонна, то ряд Фурье сход-ся и его сумма равна самой ф-цииS(x)=f(x) в т. непрерывности, а в т. разрыва, сумма будет равна S(x) = (f(  )+ f( )+ f(  ))/2, ))/2,  – т. разрыва. При чём на концах отрезка S(- – т. разрыва. При чём на концах отрезка S(-  )=S( )=S(  )= (f( )= (f(  )+ f( )+ f(  ))/2.f(x)= ))/2.f(x)=  + +  При выполн. усл. т Дирихле, ряд Фурье для ф-ции f(x) имеет вид .f(x)= При выполн. усл. т Дирихле, ряд Фурье для ф-ции f(x) имеет вид .f(x)=  + +  . .
11.Ряды Фурье для четных и нечетных функций:f(x)-четная , если f(-x)=f(x); f(x)-нечетная, f(-x)=-f(x); А)f(x)-четная ►  =2 =2  (1), (1),  = =  + +  = =  + +  =2 =2  ◄. Б)f(x)-нечетная; ◄. Б)f(x)-нечетная;  . Учитываем функции 1 и 2. Ряд Фурье для чётных ф-ций будет содержать только cos: f(x)-четная: f(x)= . Учитываем функции 1 и 2. Ряд Фурье для чётных ф-ций будет содержать только cos: f(x)-четная: f(x)=  + +  = =  ; ;
{an=  n=0,1,2,… ; bn=0}. f(x)-нечетная: f(x)= n=0,1,2,… ; bn=0}. f(x)-нечетная: f(x)=  ; { an=0 ;bn= ; { an=0 ;bn=  n=0,1,2,… }. n=0,1,2,… }.
|


 наз. знакоперем, если среди его элементов имеются как полож так и отрицательные. Опр:Если знакополож ряды могут сход и расход, то знакопеременный ряд наз абсолютносходящимся, если ряд составленный из модулей или абсолютнх величин
наз. знакоперем, если среди его элементов имеются как полож так и отрицательные. Опр:Если знакополож ряды могут сход и расход, то знакопеременный ряд наз абсолютносходящимся, если ряд составленный из модулей или абсолютнх величин  сход Опр: Ряд
сход Опр: Ряд  расход, а
расход, а  =a1-a2+a3-a4+… ; an≥0, ∀n. Признак Лейбница: если в знакочеред. Ряде элем. таковы, что выполн.условия: 1) a1>a2>a3>…>an>… 2)
=a1-a2+a3-a4+… ; an≥0, ∀n. Признак Лейбница: если в знакочеред. Ряде элем. таковы, что выполн.условия: 1) a1>a2>a3>…>an>… 2)  =0 , то ряд
=0 , то ряд  ) ►Докажем, что сущ.
) ►Докажем, что сущ.  , т.к.
, т.к.  >0, то Sn>0,∀n.
>0, то Sn>0,∀n. =a1-(a2-a3)-( a4-a5)…-a2m<a1 , S2m<a1 , послед-ть {Sn}положительна, возрастает и непревосходит a1, тоесть ограничена сверху, а значит имеет предел, т.к. сущ.
=a1-(a2-a3)-( a4-a5)…-a2m<a1 , S2m<a1 , послед-ть {Sn}положительна, возрастает и непревосходит a1, тоесть ограничена сверху, а значит имеет предел, т.к. сущ.  =S =>сущ. .
=S =>сущ. .  =.
=.  S=>сущ. .
S=>сущ. .  где
где  (x)–фун-ции определённые на множ-ве X. Опр.Возьмем
(x)–фун-ции определённые на множ-ве X. Опр.Возьмем  ∈X и подставим в
∈X и подставим в  ,
,  получим числовой ряд, если он сход-ся, то говорят что
получим числовой ряд, если он сход-ся, то говорят что  Если члены ряда удовлетвор. нер-ву
Если члены ряда удовлетвор. нер-ву  <=
<=  где
где  где
где  –числа назыв коэффиц ряда наз степенными рядами. Ряд (1) наз рядом по степеням x, ряд (2)- рядом по степ
–числа назыв коэффиц ряда наз степенными рядами. Ряд (1) наз рядом по степеням x, ряд (2)- рядом по степ 
 сводится к ряду (1), поэтому будем рассматривать ряд (1)
сводится к ряду (1), поэтому будем рассматривать ряд (1) сход в некоторой точке
сход в некоторой точке  , тогда он сход абсолютно для любого xудовл-его неравенству
, тогда он сход абсолютно для любого xудовл-его неравенству  и равномерно для любого xудовл
и равномерно для любого xудовл  где gнекоторое число. Если же ряд расход в точке
где gнекоторое число. Если же ряд расход в точке  , то он будет расход для всех x удовл нер-во
, то он будет расход для всех x удовл нер-во  ►Пусть степ-ой ряд сход в т.
►Пусть степ-ой ряд сход в т.  =>по необход признаку сравн сход
=>по необход признаку сравн сход  . Согласно св-м сходимости послед-ей , после-ть
. Согласно св-м сходимости послед-ей , после-ть  будет ограничена, т.е. ∃ M>0, что
будет ограничена, т.е. ∃ M>0, что  преобраз исходн ряд след образом
преобраз исходн ряд след образом  . С учетом нер-ва
. С учетом нер-ва  получ след нер-ва
получ след нер-ва  (3)пусть
(3)пусть  ,
,  будет геом прогрессией со знаменателем
будет геом прогрессией со знаменателем  будет сходиться. И из нер-ва (3) и признака сравн следует что ряд
будет сходиться. И из нер-ва (3) и признака сравн следует что ряд  сход абсолютно◄Радиус сход для степ ряда (1): 1) применим признак Даламбера
сход абсолютно◄Радиус сход для степ ряда (1): 1) применим признак Даламбера  2)прим радикальный призн Коши:
2)прим радикальный призн Коши: 
 г) записываем оконч ответ
г) записываем оконч ответ в) исслед сход на концах инт-ла
в) исслед сход на концах инт-ла  г) записываем оконч ответ Св-ва:Степенные ряды внутри инт-ла сход можно складывать,перемножать, диф-вать и интегрировать
г) записываем оконч ответ Св-ва:Степенные ряды внутри инт-ла сход можно складывать,перемножать, диф-вать и интегрировать (x-x0)+
(x-x0)+  (x-x0)2+…+
(x-x0)2+…+  (x-x0)n+Rn(x);
(x-x0)n+Rn(x); f(c); x0<c<x. Если x0=0, то получ. Частный случ. Ф-ции Тейлора, а именно ф-ция Маклорена: f(x)=Pn(x)+Rn(x) , если
f(c); x0<c<x. Если x0=0, то получ. Частный случ. Ф-ции Тейлора, а именно ф-ция Маклорена: f(x)=Pn(x)+Rn(x) , если  =0, то
=0, то  =
=  =f(x), то из ф-ции Тейлора получ. ряд Тейлора, т.к. Pn(x) представляет собой n-ую частичную сумму. Т:Для того чтобы ряд Тейлора сходился и его сумма S(x)=f(x) <=> чтобы
=f(x), то из ф-ции Тейлора получ. ряд Тейлора, т.к. Pn(x) представляет собой n-ую частичную сумму. Т:Для того чтобы ряд Тейлора сходился и его сумма S(x)=f(x) <=> чтобы  -
-  +
+  -…=
-…=  ;Найти интервал сходимости:
;Найти интервал сходимости:  =x2*
=x2*  =0<1 – сход. ∀x ∈ R -> интервал сход. (-∞;∞). 2)sinx=1-
=0<1 – сход. ∀x ∈ R -> интервал сход. (-∞;∞). 2)sinx=1-  +
+  +…=
+…=  ;Интервал сходимости ноход. Так же как и в 1 и он представляет собой всю сисловую ось (-∞;∞). 3)
;Интервал сходимости ноход. Так же как и в 1 и он представляет собой всю сисловую ось (-∞;∞). 3)  =
=  ; Интервал сход. (-∞;∞). 4)shx=
; Интервал сход. (-∞;∞). 4)shx=  , chx=
, chx=  ; shx=
; shx=  *2(
*2(  ), (-∞;∞);chx=
), (-∞;∞);chx=  +…+
+…+  , (-∞;∞). 5)
, (-∞;∞). 5)  =
=  =1+x+x2+..+xn+… ,|x|<1 (-1;1);
=1+x+x2+..+xn+… ,|x|<1 (-1;1);  =1-x+x2-x3=
=1-x+x2-x3=  , (-1;1). 6)
, (-1;1). 6)  =-
=-  =-
=-  -
-  )
)  =-
=-  ; |x|<1, [-1;1).
; |x|<1, [-1;1). Взяв достаточное число первых членов ряда, получим приближ. рав-во
Взяв достаточное число первых членов ряда, получим приближ. рав-во  Точность этого рав-ва увелич-ся с возрастанием n. Для того чтобы обеспеч. заданную точность, мы оцениваем по модулю одно из слогаемых ряда, которое меньше Eи берём сумму предыдущих элементов ряда. вычисл. интегр.
Точность этого рав-ва увелич-ся с возрастанием n. Для того чтобы обеспеч. заданную точность, мы оцениваем по модулю одно из слогаемых ряда, которое меньше Eи берём сумму предыдущих элементов ряда. вычисл. интегр.  ,E=
,E=  , разложим подынтегральную функциюв степенной ряд
, разложим подынтегральную функциюв степенной ряд  =1+t/1! +t^2/2!+…+t^n/n!+.. Вместо заданной подынтегральной функции будем интегрировать в заданных пределах степенной ряд.Отбрасывая все члены ряда, которые больше E, после подстановки пределов интегрирования, получим
=1+t/1! +t^2/2!+…+t^n/n!+.. Вместо заданной подынтегральной функции будем интегрировать в заданных пределах степенной ряд.Отбрасывая все члены ряда, которые больше E, после подстановки пределов интегрирования, получим  =(x+
=(x+  )|
)|  =(1-1/3+1/10-1/42+(1/216)<E-..)
=(1-1/3+1/10-1/42+(1/216)<E-..)  1-1/3+1/10-1/42=0,743.вычисл. диф. урав.y”=F(x,y,y’), {y(
1-1/3+1/10-1/42=0,743.вычисл. диф. урав.y”=F(x,y,y’), {y(  ; y’(
; y’(  } –нач. усл;
} –нач. усл;  - заданные знач. Будем искать решен. д.у. y(x) в виде степенного ряда (*) - y(x)=y(
- заданные знач. Будем искать решен. д.у. y(x) в виде степенного ряда (*) - y(x)=y(  *(x-
*(x- 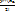 *(x-
*(x-  ;y’’’(
;y’’’(  +
+  (1).Для вычисл-ия коэф. тригон ряда нам нужны некот. ф-лы
(1).Для вычисл-ия коэф. тригон ряда нам нужны некот. ф-лы  =
=  =
=  ;
;  =
=  ;
; =
=  =
=  все эти ф-лы = (2)
все эти ф-лы = (2) на интервале [-
на интервале [-  ], иудовлетв. условиям:1)кусочно-монотонная, т.е. может иметь конечное число точек разрыва первого рода. 2)кусочно-монотонна, то ряд Фурье сход-ся и его сумма равна самой ф-цииS(x)=f(x) в т. непрерывности, а в т. разрыва, сумма будет равна S(x) = (f(
], иудовлетв. условиям:1)кусочно-монотонная, т.е. может иметь конечное число точек разрыва первого рода. 2)кусочно-монотонна, то ряд Фурье сход-ся и его сумма равна самой ф-цииS(x)=f(x) в т. непрерывности, а в т. разрыва, сумма будет равна S(x) = (f(  )+ f(
)+ f(  ))/2,
))/2,  – т. разрыва. При чём на концах отрезка S(-
– т. разрыва. При чём на концах отрезка S(-  )+ f(
)+ f(  ))/2.f(x)=
))/2.f(x)=  +
+  При выполн. усл. т Дирихле, ряд Фурье для ф-ции f(x) имеет вид .f(x)=
При выполн. усл. т Дирихле, ряд Фурье для ф-ции f(x) имеет вид .f(x)=  =2
=2  (1),
(1),  +
+  . Учитываем функции 1 и 2. Ряд Фурье для чётных ф-ций будет содержать только cos: f(x)-четная: f(x)=
. Учитываем функции 1 и 2. Ряд Фурье для чётных ф-ций будет содержать только cos: f(x)-четная: f(x)=  +
+  =
=  ;
; n=0,1,2,… ; bn=0}. f(x)-нечетная: f(x)=
n=0,1,2,… ; bn=0}. f(x)-нечетная: f(x)=  ; { an=0 ;bn=
; { an=0 ;bn=  n=0,1,2,… }.
n=0,1,2,… }.