
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ряды Фурье 2l-периодических функций.Ф-я f(x) задана на инт-ле { Замеч: В случае четности ил нечетн ф-ции формулы для вычисл коэф-тов упрощаются:
13.Разложен в ряд Фурье непериодич. функций:Пусть ф-ция f(x) задана на промежутке [0; Комплексная форма ряда Фурье
Определение ф-ции комплексной перем.Предел, непрерывность. Опр.Функция компл. перем-ой – это правило, по которому каждому комплексному знач. независ. переменной (из области опред-ия) соответствует одно и только одно комплексное значение функцииПусть дано некоторое мн-во D-точек комплексной пл-ти.Опр. Окрестностью (.) |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 497. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и удовл усл-ям т.Дирихле, тогда её можно разл в ряд Фурье вида:
и удовл усл-ям т.Дирихле, тогда её можно разл в ряд Фурье вида:  коэф-ы опред ф-ми:
коэф-ы опред ф-ми: }
} -четная:
-четная:  -нечетн:
-нечетн: 
 ]. Чтобы разложить такую ф-цию в ряд Фурье необход. сделать её переодической, для этого заданную ф-цию необходимо продолжить на промежутке [-π;0] , либо четным , либо нечетным образом: a)четное положение
]. Чтобы разложить такую ф-цию в ряд Фурье необход. сделать её переодической, для этого заданную ф-цию необходимо продолжить на промежутке [-π;0] , либо четным , либо нечетным образом: a)четное положение  б)нечетное
б)нечетное  . Вывод: В зависимости от вида продолжения(чет/нечет) одна и та же ф-ция м.б. представлена разным образом(по sin/cos).
. Вывод: В зависимости от вида продолжения(чет/нечет) одна и та же ф-ция м.б. представлена разным образом(по sin/cos).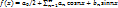 представим
представим  ф-ми Эйлера{
ф-ми Эйлера{  }
}  =
= 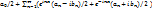 =
=  =
= 
 –комплексная форма ряда Фурье. Элементы ряда наз. комплексными гармоническими коэф ряда – комплексными амплитудами
–комплексная форма ряда Фурье. Элементы ряда наз. комплексными гармоническими коэф ряда – комплексными амплитудами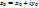 будем называть круг достаточно малого радиуса с центром в этой точке. 0<|z-
будем называть круг достаточно малого радиуса с центром в этой точке. 0<|z-  |<E, (.)
|<E, (.)  наз-ся граничной точкой мн-ва D, если её окрестность содержит как точки мн-ва Dтак и точки непринадл. мн-ву D.(.)
наз-ся граничной точкой мн-ва D, если её окрестность содержит как точки мн-ва Dтак и точки непринадл. мн-ву D.(.)  наз-ся внешней, если её окрестность не содержит точки этого мн-ва.Опр.Мн-во всех гранич точек – граница. Если мн-во содержит все свои гранич точки, то наз-ся замкнутой D.В дальнейшем рассматриваем мн-во огранич. гладким замкнутым контуромОпр.Областью наз-ся мн-во Dобладающее 2-мя св-вами: открытость, связность. Открытость означает, что Dсостоит только из внутренних точек. Связность означает, что любые 2 точки области можно соединить непрерывной гладкой кривой целиком лежащей в этой области. Окрестносью бесконечности наз-ся мн-во точек пл-тиz, определяемое неравенством |z|>R, R-сколь угодно большое число. В зависимости от вида границ области, различают: односвязные , 2хсвязные,3-х связные области ..Опр.Число A≠∞, наз-ся пределом ф-цииf(z)
наз-ся внешней, если её окрестность не содержит точки этого мн-ва.Опр.Мн-во всех гранич точек – граница. Если мн-во содержит все свои гранич точки, то наз-ся замкнутой D.В дальнейшем рассматриваем мн-во огранич. гладким замкнутым контуромОпр.Областью наз-ся мн-во Dобладающее 2-мя св-вами: открытость, связность. Открытость означает, что Dсостоит только из внутренних точек. Связность означает, что любые 2 точки области можно соединить непрерывной гладкой кривой целиком лежащей в этой области. Окрестносью бесконечности наз-ся мн-во точек пл-тиz, определяемое неравенством |z|>R, R-сколь угодно большое число. В зависимости от вида границ области, различают: односвязные , 2хсвязные,3-х связные области ..Опр.Число A≠∞, наз-ся пределом ф-цииf(z)  , если Ɐε>0∃δ=δ(ε), то Ɐzудовлетвор. 0<|z-
, если Ɐε>0∃δ=δ(ε), то Ɐzудовлетвор. 0<|z-  Опр.Бесконечно удаленная (.) наз-ся
Опр.Бесконечно удаленная (.) наз-ся  =∞, если для Ɐzϵ
=∞, если для Ɐzϵ  соотв. значениеf(z) ϵU(∞)принадлеж. окрестности бесконечно удалённой точки. Опр. (.)
соотв. значениеf(z) ϵU(∞)принадлеж. окрестности бесконечно удалённой точки. Опр. (.)  =
= 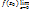 или
или  Δ ɯ=0; Δ ɯ =f(z)-f(
Δ ɯ=0; Δ ɯ =f(z)-f(  Если ф-ция непрерывна в каждой точке некот. множ-ва то она наз-ся непрерывной на данном множ-ве Опр.точками разрыва наз-ся точки комплексной области zв которых нарушается условие неприрывности.
Если ф-ция непрерывна в каждой точке некот. множ-ва то она наз-ся непрерывной на данном множ-ве Опр.точками разрыва наз-ся точки комплексной области zв которых нарушается условие неприрывности.