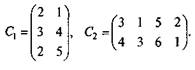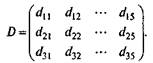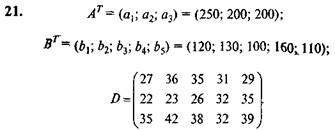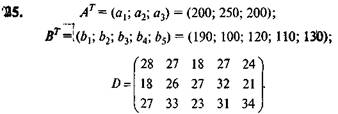Расчет точки безубыточности

Студопедия

КАТЕГОРИИ:

Авто Автоматизация Архитектура Астрономия Аудит Биология Бухгалтерия Военное дело Генетика География Геология Государство Дом Журналистика и СМИ Изобретательство Иностранные языки Информатика Искусство История Компьютеры Кулинария Культура Лексикология Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлы и Сварка Механика Музыка Население Образование Охрана безопасности жизни Охрана Труда Педагогика Политика Право Приборостроение Программирование Производство Промышленность Психология Радио Регилия Связь Социология Спорт Стандартизация Строительство Технологии Торговля Туризм Физика Физиология Философия Финансы Химия Хозяйство Ценнообразование Черчение Экология Эконометрика Экономика Электроника Юриспунденкция

Затраты на ТО и ремонт одного автомобиля, тыс. руб.

Затраты на транспортировку,

тыс. руб.

Производственная мощность, шт.

Прогнозируемое количество ТО, ед.

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Фирма «Север» владеет сетью складских помещений, сдаваемых в аренду организациям, занимающимся оптовой торговлей. Проведенный анализ рынка транспортных услуг города показал, что можно создать собственный парк транспортных средств. Прогнозируемый объем транспортной работы (Р); постоянные затраты (FС), связанные с содержанием парка транспортных средств; переменные затраты (z) на единицу транспортной работы и транспортный тариф (T) на один тонно – километр приведены в табл. 3.22. Необходимо определить с помощью «точки безубыточности» целесообразность создания парка подвижного состава:

в стоимостном выражении;

в натуральном выражении.

Таблица 3.22

Данные о работе фирмы

Номер варианта	Р, ткм	FC, у. д. е.	z, у. д. е. / ткм	Т, у. д. е. / ткм
1	300	3700	57	68
2	316	4063	58	73
3	334	4461	61	77
4	352	4898	63	81
5	371	5378	66	85
б	392	5300	68	89
7	413	5224	71	93
8	436	5149	74	92
9	460	5075.	77	91
10	469	5002	80	94
11	478	4930	83	97
12	488	4859	86	96
13	550	5430	152	168
14	420	5628	158	174
15	435	5009	140	155
16	420	4458	125	138
17	370	3968	111	123
18	395	3531	99	109
19	430	3143	88	97
20	270	2797	78	87
21	297	2895	82	92
22	327	2996	86	98
23	359	3134	90	105
24	395	3277	94	112
25	195	3427	98	ИЗ
26	215	3584	94	114
27	236	3710	89	115
28	260	3839	93	116
29	285	3974	98	117
30	314	4113	102	118

Принятие решений в условиях определенности

Показатели эффективности работы предприятий приведены в следующей таблице. Необходимо определить наиболее эффективно работающее предприятие с учетом четырех критериев (табл. 3.23, 3.24).

Таблица 3.23

Критерии оценки эффективности работы предприятий

Номер предприятия	Показатели эффективности работы предприятия, у. е.
Номер предприятия	прибыль	себестоимость единицы продукции (услуг)	фондоотдача	Производи-тельность
I	30,0	40,0	0,5.0	300
II	25,0	20,0	0,30	200
III	40,0	45,0	0,10	250
IV	28,0	30,0	0,40	160
V	15,0	12,0	0,25	280
VI	50,0	30,0	0,5.1	120
VII	43,0	37,0	0,33	260
Весовые коэффициенты	0,34	0,26	0,55	0,15

Таблица 3.24

Исходные данные по вариантам

Номер варианта	Номер предприятия	Номер варианта	Номер предприятия
1	I, II, III	16	I, III, IV
2	I, II, IV	17	I, Ш, V
3	I, П, V	18	I, III, VI
4	I, II, VI	19	I, III, VII
5	I, II, VII	20	II, IV, V
6	II, III, IV	21	II, IV, VI
7	II, III, V	22	II, IV, VII
8	II, III, VI	23	III, V, VI
9	II, III, VII	24	III, V, VII
10	II, V, VI,	25	I, IV, V
11	II, V, VII	26	I, IV, VI
12	II, VI, VII	27	I, IV, VII
13	III, IV, V	28	I, V VI
14	III, IV, VI	19	I, V, VII
15	III, IV, VII	30	I, VI, VII

Анализ и принятие решений в условиях неопределенности

Определите модель подвижного состава, которую необходимо приобрести для удовлетворения транспортных услуг промышленных предприятий (табл. 3.25). Множество возможных стратегий в задаче включает следующие параметры:

R₁ – бортовой автомобиль КамАЗ – 5320 (грузоподъемность – 8 т);

R₂ – бортовой автомобиль МАЗ – 5335 (грузоподъемность – 8 т);

R₃ – бортовой автомобиль «Урал – 377» (грузоподъемность – 7,5 т).

Затраты, связанные с ремонтом данного парка транспортных средств, зависят от влияния случайных факторов, образующих множество состояний природы S (I = 1…7). Результаты расчета экономических затрат приведены в таблице:

Модель подвижного состава	Состояние природы
Модель подвижного состава	S₁	S₂	S₃	S₄	S₅	S₆	S₇
R₁	40	70	30	25	45	65	55
R₂	60	50	45	20	30	35	40
R₃	50	30	40	35	60	55	45

Таблица 3.25

Исходные данные по вариантам

Номер варианта	Состояние природы	Номер варианта	Состояние природы
1	1,2,3,4	16	2, 4, 5, 6
2	1,2,3,5,	17	2, 4, 5,7
3	1, 2, 3, 6	18	3, 4, 5, 6
4	1,2,3,7	19	3, 4, 5, 7
5	1, 3, 4, 5	20	3, 5, 6, 7
6	1,3,4,6	21	4, 5, 6, 7
7	1, 3, 4, 7	22	1,2,4,5
8	1,3,5,6	23	1, 2, 4, 6
9	1,3,5,7	24	1,2,4,7
10	1, 4, 5, 6	25	1,2,5,6
11	1, 4, 5, 7	26	1,2,5,7
12	1,5,6,7	27	1,2,6,7
13	2, 3, 4, 5	28	2, 5, 6, 7
14	2, 3, 4, 6	29	1,3,6,7
15	2, 3, 4, 7	30	1, 4, 6, 7

Анализ и принятие решений в условиях риска

После введения в действие новой линии производственного оборудования и увеличения объемов производства руководство фирмы «Кондор» решило расширить границы сбыта своей продукции. Службой логистики был проведен анализ различных вариантов создания системы товародвижения. В результате этого анализа были отобраны три наиболее привлекательных варианта, которые различаются между собой отдельными элементами (вид транспорта, перевозчик, оптовые базы и склады и т. п.). Затраты по организации систем одинаковые.

Планируемая прибыль (тыс. у. д. е.) от функционирования каждой из систем представлена в виде распределения вероятностей его значений (табл. 3.26). Требуется опередить оптимальный вариант системы товародвижения (табл. 3.27).

Таблица 3.26

Распределение вероятностей получения прибыли

Варианты системы	В числителе – прибыль; в знаменателе – вероятность
1	3200	3830	4460	5090	5720	6350	6980
1	0,05	0,10	0,20	0,30	0,20	0,10	0,05
2	7600	8080	8560	9040	9520	–	–
2	0,12	0,22	0,32	0,22	0,12	–	–
3	3600	4520	5440	6360	7280	8200	9120
3	0,06	0,11	0,19	0,28	0,19	0,11	0,06
4	5300	5750	6200	6650	7100	7550	–
4	0,10	0,15	0,25	0,25	0,15	0,10	–
5	1500	2450	3400	4350	–	–	–
5	0,20	0,30	0,30	0,20	–	–	–
6	11230	12150	13070	13990	14910	15830	16750
6	0,07	0,12	0,18	0,26	0,18	0,12	0,07
7	8930	9770	10610	11450	12290	13130	–
7	0,07	0,18	0,25	0,25	0,18	0,07	–
8	2400	3250	4100	4950	5800	–	–
8	0,12	0,23	0,30	0,23	0,12	–	–

Таблица 3.27

Исходные данные по вариантам

Номер варианта	Варианты системы	Номер варианта	Варианты системы
1	1,2,3	16	1,2,4
2	2,3,4	17	1,2,5
3	3,4,5	18	1,2,6
4	4,5,6	19	1,2,7
5	5,6,7	20	1,2,8
6	6,7,8	21	4,5,6
7	2,3,5	22	4,5,7
8	2,3,6	23	4,5,8
9	2,3,7	24	5,6,7
10	2,3,8	25	5,6,8
11	3,4,6	26	1,4,5
12	3,4,7	27	1,5,6
13	3,4,8	28	1,6,7
14	4,5,7	29	2,5,6
15	4,5,8	30	2,5,7

Оценка эффективности инвестиционного проекта

Фирма «Гермес», выпускающая бытовую электротехнику, для завоевания новых рынков сбыта и увеличения доли на рынке предполагает открыть крупный торговый центр в соседнем регионе. Торговый центр будет включать: магазины по продаже бытовой техники и сервисные службы по оказанию гарантийного и послегарантийного обслуживания.

Совокупные затраты на открытие торгового центра составляют I₀. В течение первых n лет предполагается поступление чистых доходов в размере CF_t (t = 1…n) (табл. 3.28). Необходимо при принятой норме дисконта r определить экономическую эффективность открытия торгового центра с помощью:

показателя чистой современной стоимости;

индекса рентабельности.

Таблица 3.28

Характеристика инвестиционных проектов

Номер варианта	I₀, млн у. д. е.	r, %	CF_t, млн у. д. е. по годам
Номер варианта	I₀, млн у. д. е.	r, %	1	2	3	4	5	6
1	120000	15	32400	37200	42000	46800	52800	56400
2	120000	17	30240	34720	39200	43680	49280	52640
3	150000	17	38340	44020	49700	55380	62480	66740
4	150000	19	43740	50220	56700	63180	71280	–
5	17000	13	4914	5642	6425	771	8008	8408
6	21000	16	4914	5642	6425	7171	8008	–
7	270000	12	56784	58422	60424	62790	65702	71526
8	250000	12	65520	67410	69720	72450	75810	82530
9	250000	16	56700	65100	73500	81900	92400	102900
10	160000	16	56700	65100	73500	81900	–	–
11	120000	19	56700	65100	73500	81900	–	–
12	120000	19	51840	59520	67200	74880	84480	94080
13	160000	9	51840	59520	67200	74880	84480	94080
14	190000	21	51840	59520	67200	74880	84480	–
15	20910	16	5972	6857	7808	8715	9733	10219
16	25830	20	5972	6857	7808	8715	9733	–
17	332100	15	69013	71004	73437	76312	79852	86930
18	307500	15	79630	81927	84735	88053	92136	100304
19	250000	20	68911	79120	89329	99538	112299	125061
20	196800	20	68911	79120	89329	99538	–	–
21	147600	24	68911	79120	89329	99538	–	–
22	147600	24	63004	72338	81672	91006	102674	114341
23	24000	16	4816	5529	6296	7027	7848	8240
24	20000	13	5405	6206	7067	7888	8809	–
25	216000	13	55648	57254	59216	61534	^ 64388	70095
26	162000	13	64210	66062	68326	71001	74294	80879
27	162000	18	55566	63798	72030	80262	90552	100842
28	291600	17	54535	56108	58031	60304	63100	68694
29	218700	15	70631	72668	75158	78101	81723	88967
30	216000	19	54455	62522	70589	78657	88741	98825

Транспортная задача

Составление оптимального плана перевозок

Вариант 1. В пунктах A и В находится соответственно 150 и 90 т горючего. Пунктам 1, 2, 3 требуется соответственно 60, 70, 110 т горючего. Стоимость перевозки 1 т горючего из пункта A в пункты 1, 2, 3 равна 60, 10, 40 тыс. руб. за 1 т соответственно, а из пункта В в пункты 1, 2, 3 – 120, 20, 80 тыс руб. за 1 т соответственно. Составить план перевозок горючего, минимизирующий общую сумму транспортных расходов.

Вариант 2. Три завода выпускают грузовые автомобили, которые отправляются четырем потребителям. Первый завод поставляет 90 платформ грузовиков, второй – 30, третий – 40 платформ. Для потребителей требуется: первому – 70 платформ, второму – 30, третьему – 20, четвертому – 40 платформ. Стоимость перевозки одной платформы между каждым поставщиком и каждым потребителем (у. д. е.) указана в табл. Составить оптимальный план доставки грузовых автомобилей.

Поставщик	Потребитель
	1	2	3	4
I	18	20	14	10
II	10	20	40	30
III	16	22	10	20

Вариант 3. При строительстве магистральной дороги необходимо выровнять имеющиеся на трассе выбоины до уровня основной дороги и срезать в некоторых местах выступы. Срезанным грунтом заполняются выбоины. Перевозка грунта осуществляется грузовиками одинаковой грузоподъемности. Расстояние в километрах от срезов до выбоин и объем работ указаны в табл. Составить план перевозок, минимизирующий общий пробег грузовиков.

Поставщик	Потребитель			Наличие грунта, т
	I	II	III
А	1	2	3	110
В	2	1	3	130
С	1	2	4	20
Требуемое количество грунта, т	100	140	60

Вариант 4. Груз, хранящийся на трех складах и требующий для перевозки 60, 80,106 автомашин соответственно, необходимо перевезти в четыре магазина. Первому магазину требуется 44 машины груза, второму – 70, третьему – 50 и четвертому – 82 машины. Стоимость пробега одной автомашины за 1 км составляет 10 тыс. руб. Расстояние между складами и магазинами указаны в табл. Составить оптимальный по стоимости план перевозки груза из складов в магазины.

Склад	Магазин
	1	2	3	4
1	13	17	6	8
2	2	7	10	41
3	12	18	2	22

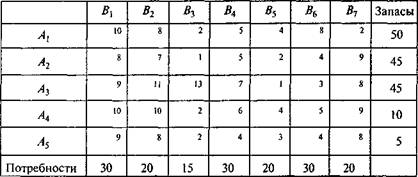
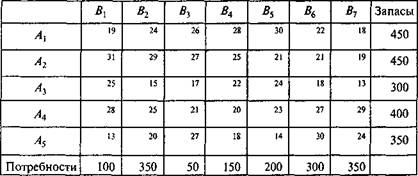
Вариант 5. На складах А, В, С находится сортовое зерно соответственно в количестве 100, 150, 250 т, которое нужно доставить в четыре пункта. Пункту 1 необходимо 50 т, пункту 2 – 100, пункту 3 – 200, пункту 4 – 150 т. Стоимость доставки 1 т зерна со склада А в указанные пункты соответственно равна 80; 30; 50; 20 тыс. руб.; со склада В – 40; 10; 60; 70 тыс., со склада С – 10; 90; 40;30 тыс. руб. Составить оптимальный план перевозки зерна при условии минимума стоимости перевозки.

Вариант 6. Завод имеет три цеха А, В, С и четыре склада 1; 2; 3; 4. Цех А производит 30 тыс. изделий, цех 5 – 40 тыс.; цех С – 20 тыс. изделий. Пропускная способность складов за то же время характеризуется следующими показателями: склад 1 – 20 тыс. изделий, склад 2 – 30 тыс.; склад 3 – 30 тыс. и склад 4 – 10 тыс. изделий. Стоимость перевозки 1 тыс. изделий из цеха А в склады 1; 2; 3; 4 соответственно 20; 30; 40; 40 тыс. руб., из цеха В за 1 тыс. изделий соответственно равна 30; 20; 50; 10 тыс. руб., а из цеха С – соответственно 40; 30; 20; 60 тыс. руб. Составить такой план перевозки изделий, при котором расходы на перевозку всех90 тыс. изделий были бы наименьшими.

Вариант 7. На строительном полигоне имеется пять кирпичных заводов, объем производства которых в сутки равен 600; 600; 500; 650; 700 т. Эти заводы удовлетворяют потребностям семи строительных объектов соответственно в количестве 350; 450; 300; 450; 300; 200; 450 т. Оставшийся кирпич отправляют по железной дороге в другие районы. Кирпич на строительные объекты доставляется автомобильным транспортом. Расстояние в километрах от заводов до объектов приведено в табл. Определить, с каких заводов и на какие объекты должен доставляться кирпич, а также какие заводы и в каком количестве должны отправлять кирпич в другие районы, чтобы транспортные издержки по доставке кирпича автотранспортом были минимальными.

Стоимость перевозки 1 т кирпича автотранспортом удовлетворяет условию

с = а + d (l – 1),

где а = 25 тыс. руб., d = 5 тыс. руб., l – пробег, км.

Завод	Объект
	B₁	В₂	В₃	B₄	B₅	B₆	B₇
A₁	14	5	10	8	16	10	25
А₂	13	4	11	9	20	12	23
A₃	18	8	14	18	23	13	21
А₄	14	7	13	19	15	16	23
А₅	11	15	14	25	19	15	20

Вариант 8. Имеется две станции технического обслуживания (СТО), выполняющие ремонтные работы для трех автопредприятий. Производственные мощности СТО в условных единицах (у. ед.), стоимость ремонта 1 у. ед. в различных СТО, затраты на транспортировку 1 у. ед. из автопредприятий на СТО и обратно и прогнозируемое количество ремонтов в планируемом периоде на каждом автопредприятии (в у. ед.) приведены в табл. Требуется найти, какое количество автомашин (в у. ед.) из каждого автопредприятия необходимо отремонтировать на каждой СТО, чтобы суммарные расходы на ремонт и транспортировку были минимальными.

Номер СТО	Стоимость ремонта 1 у ед., тыс. руб.	Затраты на транспортировку, тыс. руб.			Производственная мощность, у. ед.
		АТП – 1	АТП – 2	АТП – 3
1	520	60	70	20	10
2	710	40	50	30	8
Необходимое количество ремонтов, у. ед.		6	7	5	18

Вариант 9. Найти оптимальный план распределения заявок на ремонт для условий, приведенных в табл.

Вариант 10. Имеется два хранилища с однородным продуктом, в которых сосредоточено 200 и 120 т продукта соответственно. Продукты необходимо перевезти трем потребителям в количестве 80, 100 и 120 т каждому. Расстояния от хранилищ до потребителей (8 км) указаны в табл. Затраты на перевозку 1 т продукта на 1 км постоянны и равны 5 тыс. руб. Определить план перевозок продукта из хранилищ к потребителям при условии минимизации транспортных расходов.

Хранилище	Потребитель
	1	2	3
1	20	30	50
2	60	20	40

Вариант 11. Промышленный концерн имеет два завода и пять складов в различных регионах страны. Каждый месяц первый завод производит 40 у. ед. продукции, второй – 70 у. ед. Вся продукция, производимая заводами, должна быть направлена на склады. Вместимость первого склада – 20 у. ед.; второго – 30; третьего – 15; четвертого – 27; пятого – 28 у. ед. продукции. Издержки транспортировки с завода на склад (у. ед.) приведены в табл. Распределить план перевозок из условия минимизации ежемесячных расходов на транспортировку.

Завод	Склад
	1	2	3	4	5
1	520	480	650	500	720
2	450	525	630	560	750

Вариант 12. Три нефтеперерабатывающих завода с суточной производительностью в 10; 8; и 6 млн галлонов бензина снабжают три бензохранилища, спрос которых составляет 6; 11 и 7 млн галлонов. Бензин транспортируется в бензохранилища по трубопроводу. Стоимость перекачки бензина на 1 км составляет 5 тыс. руб. на 100 галлонов. В табл. показано, что завод 1 не связан с хранилищем 3. Сформулируйте соответствующую транспортную задачу и решите на минимум транспортных затрат.

Завод	Бензохранилище
	1	2	3
1	100	150	–
2	420	180	60
3	200	280	120

Вариант 13. Три нефтеперерабатывающих завода с суточной производительностью в 8; 8; и 6 млн галлонов бензина снабжают три бензохранилища, спрос которых составляет 6; 11 и 7 млн галлонов. Бензин транспортируется в бензохранилища по трубопроводу. Стоимость перекачки бензина на 1 км составляет 5 тыс. руб. на 100 галлонов. Обязательно полное удовлетворение спроса бензохранилища 2, а недопоставки в хранилища 1 и 3 штрафуются в размере 8 тыс. руб. за каждый галлон. Сформулировать соответствующую транспортную задачу и решить на минимум издержек.

Вариант 14. Автомобили перевозятся на трейлерах из трех центров распределения пяти продавцам. Стоимость перевозки в расчете на 1 км пути, пройденного трейлером, равна 60 тыс. руб. Один трейлер может перевозить до 15 автомобилей. Стоимость перевозок не зависит от того, насколько полно загружается трейлер. В табл. указаны расстояния между центрами распределения и продавцами, а также величины, характеризующие ежемесячный спрос и объемы поставок, исчисляемые количеством автомобилей. Определить минимальные затраты на доставку автомобилей.

Центр распределения	Продавец					Объем поставок, шт.
	1	2	3	4	5
1	80	120	180	150	50	300
2	60	70	50	65	90	350
3	30	80	120	140	90	120
Спрос на автомобили, шт.	110	250	140	150	120	770

Вариант 15. В данной транспортной задаче суммарный спрос превосходит суммарный объем производства. Пусть штрафы за недопоставку единицы продукции в пункты назначения 1, 2 и 3 равны 5, 3 и 2 соответственно. Найдите оптимальное решение. Исходные данные приведены в табл.

Завод	Потребитель			Объем производства, у. ед.
	1	2	3
А₁	3	2	4	50
А₂	5	4	5	75
A₃	1	6	7	30
Потребность, у. ед.	60	40	70

Вариант 16. В данной транспортной задаче не введены штрафы и спрос пункта назначения 1 должен быть полностью удовлетворен. Сформулируйте задачу и найдите оптимальное решение. Исходные данные приведены в табл.

Завод	Потребитель			Объем производства, у. ед.
	1	2	3
А₁	3	2	4	50
А₂	5	4	5	75
A₃	1	6	7	30
Потребность, у. ед.	60	40	70

Вариант 17. В настоящей несбалансированной транспортной задаче (табл.) назначается плата за хранение каждой единицы невывезенного из исходного пункта i груза. Пусть коэффициенты стоимости хранения груза в исходных пунктах 1; 2 и 3 равны 5; 6 и 2 соответственно. Найдите оптимальное решение, если весь объем груза исходного пункта 2 должен быть вывезен для того, чтобы освободить место для новой продукции.

Пункт хранения (склады)	Потребитель			Запасы продукции, т
	1	2	3
1	1	0	4	300
2	3	1	2	400
3	1	2	1	250
Спрос, т	280	320	200

Вариант 18.Три завода производят продукцию в объемах 200, 300, 500 ед. Эта продукция необходима четырем потребителям в количестве 210, 320, 150 и 200 ед. Готовая продукция поступает потребителям через склады D₁ и D₂, емкость которых соответственно равна 500 и 300 ед. Транспортные расходы на доставку единицы продукции на склады и со складов потребителям заданы матрицами С₁ и С₂.

Необходимо составить план доставки продукции от заводов к потребителям с учетом наименьших затрат.

Вариант 19.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Найти оптимальный план закрепления потребителей за поставщиками однородного груза при условии минимизации общего пробега автомобилей.

Вариант 20.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 21. Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 22.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 23.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 24.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 25.Имеются три пункта поставки однородного груза А₁; А₂; А₃ и пять пунктов В₁; В₂; В₃; В₄; В₅ потребления этого груза. В пунктах А₁; А₂; А₃ находится груз а₁; а₂; a₃ соответственно. Груз необходимо доставить в пункты В₁; В₂; В₃; В₄; В₅ в количестве b₁; b₂; b₃; b₄; b₅ соответственно. Расстояния между пунктами заданы матрицей, км:

Вариант 26.Найти методом Фогеля план перевозок в следующей задаче

Вариант 27.Найти методом Фогеля план перевозок в следующей задаче

Вариант 28.Найти методом Фогеля план перевозок в следующей задаче

Вариант 29.Найти методом Фогеля план перевозок в следующей задаче

Вариант 30.Решить транспортную задачу, заданную в сетевой форме.

Вариант 31.Решить транспортную задачу, заданную в сетевой форме.

Вариант 32.Решить транспортную задачу, заданную в сетевой форме.

Вариант 33.Решить транспортную задачу, заданную в сетевой форме.

⇐ Предыдущая 1 234 5 Следующая ⇒

Последнее изменение этой страницы: 2018-04-12; просмотров: 1186.

stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда...