
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Особенности машинной арифметикиПри записи чисел в памяти компьютера может быть использовано только конечное, одно и то же для всех чисел одного класса (целые, действительные, комплексные) число знаков. Отсюда следует, что десятичные числа[1], введенные в память компьютера, содержат ошибку представления. На большинстве современных компьютеров принята следующая форма записи действительных чисел с плавающей точкой:
Отсюда следует: · в памяти компьютера представимо только конечное число действительных чисел; для всех остальных — округленное значение, т.е. такие числа после ввода в память компьютера содержат ошибку — ошибку представления, она называется ; машинным эпсилон, относительной точностью компьютера, машинной точностью, обозначают если · диапазон представления действительных чисел ограничен; · на машинной числовой оси действительные числа расположены неравномерно 
поскольку расстояние между двумя ближайшими числами равно 2p-t и, следовательно, увеличивается с ростом p; · при выполнении арифметических операций с действительными числами Погрешности арифметических операций Следует обратить внимание на то, что в приведенных выше неравенствах даны оценки границ погрешностей. Справедливы следующие оценки:
Докажем некоторые оценки (остальные оценки получаются аналогично).
Заметим, что если можно полагать Наибольшая потеря точности происходит при вычитании близких чисел одного знака, потеря точности не происходит при сложении чисел одного знака. Погрешность вычисления функции одного переменного Пусть Отсюда нетрудно получить оценку границы относительной погрешности вычисления функции: Для функции, заданной неявно
|
|||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 275. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
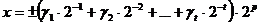 ,
,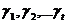 — двоичные числа, равные 0 или 1,
— двоичные числа, равные 0 или 1, 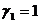 , число
, число 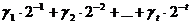 — мантисса числа x, целое p — порядок, t — разрядность,
— мантисса числа x, целое p — порядок, t — разрядность, 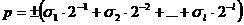 . Запись десятичного числа в памяти компьютера, для мантиссы t позиций, для порядка — l, плюс две позиции для знака числа и для знака порядка:
. Запись десятичного числа в памяти компьютера, для мантиссы t позиций, для порядка — l, плюс две позиции для знака числа и для знака порядка: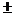
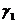
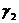
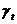
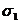
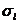
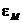 ,
, 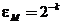 ; границу относительной ошибки представления можно вычислить:
; границу относительной ошибки представления можно вычислить: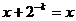 , то
, то 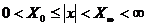 ,
, 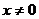 ,
,  — машинный нуль, числа меньшие по модулю чем
— машинный нуль, числа меньшие по модулю чем 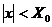 называют исчезновением порядка; не следует путать
называют исчезновением порядка; не следует путать 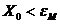 ;
; 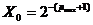 .
. 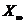 — машинная бесконечность,
— машинная бесконечность, 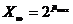 , получение числа x для которого
, получение числа x для которого 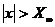 называют переполнением; для IBM PC t = 23,
называют переполнением; для IBM PC t = 23, 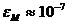 ,
, 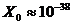 ,
, 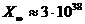 ; для инженеров важно понимать, что мантисса имеет разрядность, эквивалентную 7-14 десятичных разрядов;
; для инженеров важно понимать, что мантисса имеет разрядность, эквивалентную 7-14 десятичных разрядов;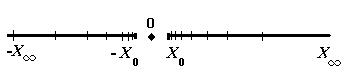
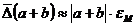 ,
, 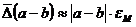 ,
, 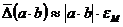 ,
, 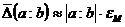 .
.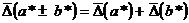 , a>0, b>0,
, a>0, b>0, ,
, 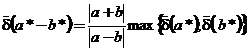 ,
,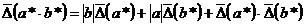 ,
,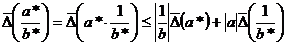
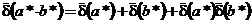 ,
, 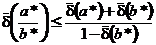 .
.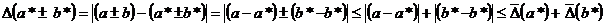
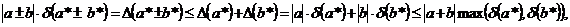
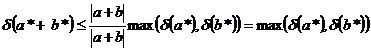 ,
,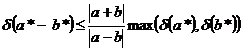 . Из последней оценки видно, что при больших значениях
. Из последней оценки видно, что при больших значениях 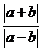 , т.е. при вычитании близких чисел возможна «катастрофическая потеря точности».
, т.е. при вычитании близких чисел возможна «катастрофическая потеря точности».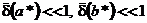 , то вместо оценок
, то вместо оценок 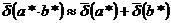 ,
, 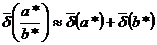 .
.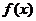 — дифференцируемая в области G (на некотором интервале, содержащем x и x*)функция, x* — приближенное значение аргумента,
— дифференцируемая в области G (на некотором интервале, содержащем x и x*)функция, x* — приближенное значение аргумента, 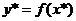 — приближенное значение функции,
— приближенное значение функции, 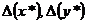 — соответствующие погрешности. Оценку погрешности
— соответствующие погрешности. Оценку погрешности 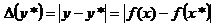 можно получить из формулы конечных приращений Лагранжа:
можно получить из формулы конечных приращений Лагранжа: 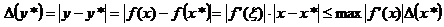 т.е. обычно полагают
т.е. обычно полагают 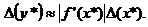
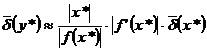 .
. :
: 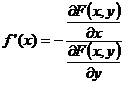 и
и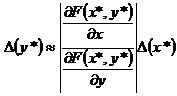 ,
, 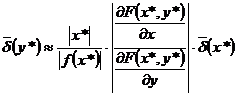 .
.