
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналитические методы решения оптимизационных задачДля реализации аналитических методов целевая функция должна быть задана аналитически. Аналитические методы могут использоваться для решения однофакторных и многофакторных задач. 1. Однофакторные задачи. Пусть целевая функция зависит от единственного аргумента. Для поиска ее экстремума (скажем, минимума) используем известные приемы математического анализа. Достаточно взять производную функции и приравнять ее к нулю, а затем решить полученное уравнение. Для определения типа экстремума (минимум, максимум или точка перегиба) потребуется также взять вторую производную. Знак второй производной указывает на тип экстремума: положительное значение говорит о том, что найден минимум, отрицательное – максимум функции.
y = f (x) → min y = 2x2 + 4x – 8 → min y'=0 4x + 4 = 0 x = -1 y''Є(- ∞; +∞ ) y'' = 0 – точка перегиба y'' < 0 – максимум функции y'' > 0 – минимум функции.
Аналитический метод для однофакторных задач предъявляет высокие требования к целевой функции: она должна быть задана аналитически и иметь 1-ю и 2-ю производные. В этом случае поиск решения может быть осуществлен методами математического анализа. 2. Многофакторные задачи. В многофакторных задачах целевая функция зависит от двух и более аргументов. F(x1, x2, …, xn) – функция нескольких переменных (≥2). Пусть, например, аналитическое выражение целевой функции имеет следующий вид:
у = 2х12 + 3х22 + 4х1 + 5х2 – 16.

Для решения воспользуемся методами математического анализа применительно к функции нескольких переменных. Возьмем частные производные по каждому аргументу и приравняем их к нулю. Получим систему уравнений, решая которую определим условия экстремума целевой функции. В нашем примере получаем систему линейных уравнений, решая которую находим условия экстремума целевой функции: х1=-1; х2=-5/6. Аналитические методы для решения многофакторных задач так же используются крайне редко, т.к.: -функция должна быть задана аналитически (иметь 1-ю и 2-ю производные); -в ходе решения задачи можно прийти к системе нелинейных уравнений, которую все равно придется решать численными, приближёнными методами.
Поисковые (численные) методы решения однофакторных Оптимизационных задач Для использования этих методов не обязательно, чтобы целевая функция была задана аналитически. Единственное требование – она должна быть вычислимой, т.е. должен быть известен способ ее вычисления (аналитическое выражение или алгоритм вычисления). Полученное решение может быть найдено с любой заданной нами точностью. Точность решения определяется лишь последующим использованием его результатов. Например, в ходе решения мы определяем оптимальную температуру проведения металлургического процесса. Понятно, что точность решения в несколько градусов нас устроит, поскольку на практике мы не сможем поддерживать температуру в печи с большей точностью, ведь регулятор температуры имеет некоторые погрешности измерения и регулирования. Для получения решения численным методом необходимо: а) задать способ вычисления целевой функции (алгоритм или аналитическое выражение): y = f (x) → min. б) все поисковые методы – приближённые, поэтому перед началом решения следует задать интересующую нас точность решения в) выбрать интервал допустимых значений оптимизирующего фактора: a≤x≤b.
1. Метод перебора (сплошного поиска).
Разбиваем ось аргументов на конечное число шагов решения, которое определяется интересующей нас точностью: Далее проводим вычисления целевой функции в точках, являющихся границами шагов, и запоминаем все результаты вычислений. Сравниваем значения целевой функции, ищем минимальное значение и определяем значение аргумента, соответствующее минимуму целевой функции. Поиск напоминает поиск наиболее глубокого места в реке. Достоинством метода является то, что он позволяет найти глобальное решение на всем интервале, если существует несколько локальных экстремумов. Недостаток – большое количество вычислений целевой функции, и, как следствие, низкая скорость. Требует запоминания всех вычисленных значений целевой функции и аргументов.
2. Метод дихотомии (половинного деления). Исходно требуется то же, что и в предыдущем методе. Разбиваем интервал значений аргумента пополам:
y1 = f (x1) y2 = f (x2).
Представим, что функция имеет один минимум на отрезке от a до b. Ординаты у1 и у2 вычислены в точках, лежащих достаточно близко друг к другу, на расстоянии удвоенной точности решения. Если у2>у1, поиск минимума на левой половине интервала теряет смысл, и ее можно отбросить. На этом первая итерация решения заканчивается, и после сокращения интервала вдвое задача вновь возвращается к исходной, но интервал дальнейшего поиска сокращается вдвое. Для сокращения интервала достаточно перенести точку а в центр первоначального отрезка, а координаты точки в оставить без изменений. Далее решение продолжается до тех пор, пока после нескольких итераций сокращенный интервал не станет меньше заданной точности. Поскольку сокращение интервала на каждой итерации происходит вдвое, то совершив 7 итераций, например, мы уменьшим первоначальный интервал в 27= 128 раз, достигнув точности решения 1/128, что менее 1% от первоначального интервала. Поскольку на каждой итерации целевая функция вычисляется дважды, общее количество ее вычислений будет равно 14. При этом нет необходимости запоминать результаты вычислений, в отличие от метода сплошного поиска. К тому же, решая задачу по методу сплошного поиска с более высокой точностью 1%, мы были бы вынуждены выполнить 100 вычислений целевой функции, и при этом все результаты вычислений надо было бы сохранить. При повышении точности решения различия методов становятся еще больше: при точности 0.5% метод дихотомии требует 16 вычислений функции, а метод сплошного поиска – 200 вычислений, при точности 0.1% - 20 и 1000 вычислений соответственно!
7 шагов Однако, метод дихотомии имеет и существенный недостаток. При наличии нескольких экстремумов целевой функции он не обеспечивает поиск глобального решения. Если желаем получить глобальное решение, то необходимо использовать метод сплошного поиска. В реальных задачах комбинируют методы.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 669. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 4х1 + 4 = 0
4х1 + 4 = 0 6х2 + 5 = 0.
6х2 + 5 = 0.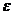 .
. . При точности 1% от интервала изменения фактора это будет соответствовать разбиению интервала на 100 шагов, при точности 5% потребуется разбить интервал на 20 шагов и т.д.
. При точности 1% от интервала изменения фактора это будет соответствовать разбиению интервала на 100 шагов, при точности 5% потребуется разбить интервал на 20 шагов и т.д.

 . Строим две дополнительные узловые точки с координатами:
. Строим две дополнительные узловые точки с координатами: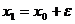
 и вычисляем значения целевой функции в этих точках.
и вычисляем значения целевой функции в этих точках.
 1
1 





